Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 của giaitoan.edu.vn. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Ở bài viết này, chúng ta sẽ cùng nhau đi sâu vào giải chi tiết các bài tập trong mục 1 trang 48, 49, 50 sách giáo khoa Toán 8. Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Đo các góc và các cạnh của tam giác \(ABC\) và tam giác \(A'B'C'\)
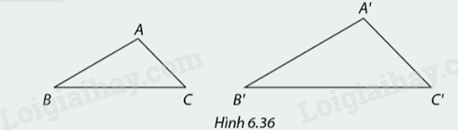
Đo các góc và các cạnh của tam giác \(ABC\) và tam giác \(A'B'C'\) trong hình 6.36. Xác định số đo góc và độ dài trong các ô?:
\(\widehat {A'} = ?\) \(\widehat {B'} = ?\) \(\widehat {C'} = ?\) \(A'B' = ?\) \(B'C' = ?\) \(A'C' = ?\)
\(\widehat A = ?\) \(\widehat B = ?\) \(\widehat C = ?\) \(AB = ?\) \(BC = ?\) \(AC = ?\)
\(\frac{{A'B'}}{{AB}} = ?\) \(\frac{{B'C'}}{{BC}} = ?\) \(\frac{{A'C'}}{{AC}} = ?\)
Em có nhận xét gì về các góc, các cạnh của tam giác \(ABC\) và tam giác \(A'B'C'\) ?
Phương pháp giải:
Đo các góc và các cạnh của tam giác \(ABC\) và tam giác \(A'B'C'\) và xác định số đo các góc và độ dài các cạnh.
Lời giải chi tiết:
\(\begin{array}{l}\widehat A = 105^\circ ;\widehat B = 30^\circ ;\widehat C = 45^\circ \\\widehat {A'} = 105^\circ ;\widehat {B'} = 30^\circ ;\widehat {C'} = 45^\circ \\AB = 2,2;AC = 1,5;BC = 3\\A'B' = 3,08;A'C' = 2,1;B'C' = 4,2\\\frac{{A'B'}}{{AB}} = \frac{5}{7};\frac{{B'C'}}{{BC}} = \frac{5}{7};\frac{{A'C'}}{{AC}} = \frac{5}{7}\end{array}\)
Các góc \(\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\)
Và các cạnh của tam giác \(ABC\) và tam giác \(A'B'C'\) có tỉ lệ tương ứng bằng nhau.
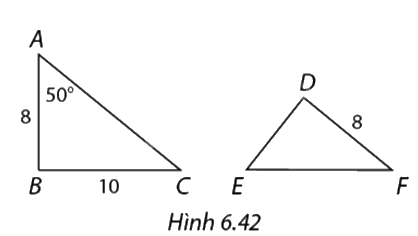
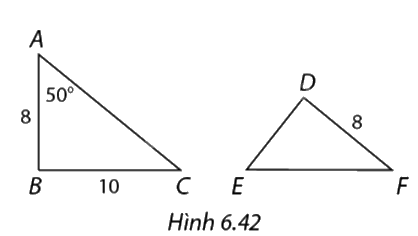
Trong hình 6.42, \(\Delta ABC\ \backsim \Delta EDF.\) Tính số đo góc \(E\) và cạnh \(DE.\)
Phương pháp giải:
Tam giác \(A'B'C'\) được gọi là đồng dạng với tam giác \(ABC\) , kí hiệu \(\Delta A'B'C'\) ∽ \(\Delta ABC\)
\(\widehat {A'} = \widehat A;\widehat {B'} = \widehat B;\widehat {C'} = \widehat C\) và \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}}\) .
Lời giải chi tiết:
Vì \(\Delta ABC\) ∽ \(\Delta EDF\) , ta có:
\(\widehat E = \widehat A = 50^\circ \)
\(\begin{array}{l}\frac{{BC}}{{DF}} = \frac{{10}}{8} = \frac{5}{4}\\ = > \frac{{AB}}{{DE}} = \frac{5}{4} \Leftrightarrow \frac{8}{{DE}} = \frac{5}{4} \Rightarrow DE = 6,4\end{array}\)
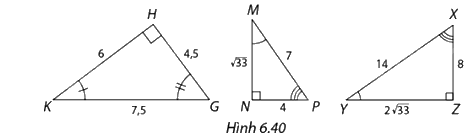
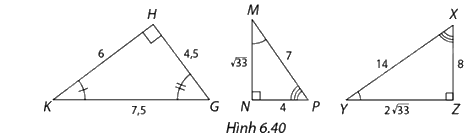
Chỉ ra các cặp tam giác đồng dạng trong Hình 6.40. Viết kí hiệu về sự đồng dạng và xác định tỉ số đồng dạng.
Phương pháp giải:
Tam giác \(A'B'C'\) được gọi là đồng dạng với tam giác \(ABC\) , kí hiệu \(\Delta A'B'C'\) ∽ \(\Delta ABC\)
\(\widehat {A'} = \widehat A;\widehat {B'} = \widehat B;\widehat {C'} = \widehat C\) và \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}}\) .
Lời giải chi tiết:
\(\Delta MNP\) ∽ \(\Delta XYZ\) , ta có:
\(\begin{array}{l}\widehat M = \widehat Y;\widehat N = \widehat Z;\widehat P = \widehat X\\\frac{{MN}}{{YZ}} = \frac{{\sqrt {33} }}{{2\sqrt {33} }} = \frac{1}{2}\\\frac{{MP}}{{XY}} = \frac{7}{{14}} = \frac{1}{2}\\\frac{{NP}}{{XZ}} = \frac{4}{8} = \frac{1}{2}\end{array}\)
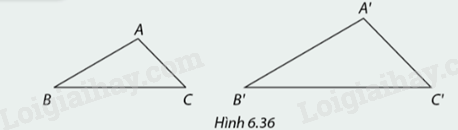
Đo các góc và các cạnh của tam giác \(ABC\) và tam giác \(A'B'C'\) trong hình 6.36. Xác định số đo góc và độ dài trong các ô?:
\(\widehat {A'} = ?\) \(\widehat {B'} = ?\) \(\widehat {C'} = ?\) \(A'B' = ?\) \(B'C' = ?\) \(A'C' = ?\)
\(\widehat A = ?\) \(\widehat B = ?\) \(\widehat C = ?\) \(AB = ?\) \(BC = ?\) \(AC = ?\)
\(\frac{{A'B'}}{{AB}} = ?\) \(\frac{{B'C'}}{{BC}} = ?\) \(\frac{{A'C'}}{{AC}} = ?\)
Em có nhận xét gì về các góc, các cạnh của tam giác \(ABC\) và tam giác \(A'B'C'\) ?
Phương pháp giải:
Đo các góc và các cạnh của tam giác \(ABC\) và tam giác \(A'B'C'\) và xác định số đo các góc và độ dài các cạnh.
Lời giải chi tiết:
\(\begin{array}{l}\widehat A = 105^\circ ;\widehat B = 30^\circ ;\widehat C = 45^\circ \\\widehat {A'} = 105^\circ ;\widehat {B'} = 30^\circ ;\widehat {C'} = 45^\circ \\AB = 2,2;AC = 1,5;BC = 3\\A'B' = 3,08;A'C' = 2,1;B'C' = 4,2\\\frac{{A'B'}}{{AB}} = \frac{5}{7};\frac{{B'C'}}{{BC}} = \frac{5}{7};\frac{{A'C'}}{{AC}} = \frac{5}{7}\end{array}\)
Các góc \(\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\)
Và các cạnh của tam giác \(ABC\) và tam giác \(A'B'C'\) có tỉ lệ tương ứng bằng nhau.
Chỉ ra các cặp tam giác đồng dạng trong Hình 6.40. Viết kí hiệu về sự đồng dạng và xác định tỉ số đồng dạng.
Phương pháp giải:
Tam giác \(A'B'C'\) được gọi là đồng dạng với tam giác \(ABC\) , kí hiệu \(\Delta A'B'C'\) ∽ \(\Delta ABC\)
\(\widehat {A'} = \widehat A;\widehat {B'} = \widehat B;\widehat {C'} = \widehat C\) và \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}}\) .
Lời giải chi tiết:
\(\Delta MNP\) ∽ \(\Delta XYZ\) , ta có:
\(\begin{array}{l}\widehat M = \widehat Y;\widehat N = \widehat Z;\widehat P = \widehat X\\\frac{{MN}}{{YZ}} = \frac{{\sqrt {33} }}{{2\sqrt {33} }} = \frac{1}{2}\\\frac{{MP}}{{XY}} = \frac{7}{{14}} = \frac{1}{2}\\\frac{{NP}}{{XZ}} = \frac{4}{8} = \frac{1}{2}\end{array}\)
Trong hình 6.42, \(\Delta ABC\ \backsim \Delta EDF.\) Tính số đo góc \(E\) và cạnh \(DE.\)
Phương pháp giải:
Tam giác \(A'B'C'\) được gọi là đồng dạng với tam giác \(ABC\) , kí hiệu \(\Delta A'B'C'\) ∽ \(\Delta ABC\)
\(\widehat {A'} = \widehat A;\widehat {B'} = \widehat B;\widehat {C'} = \widehat C\) và \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}}\) .
Lời giải chi tiết:
Vì \(\Delta ABC\) ∽ \(\Delta EDF\) , ta có:
\(\widehat E = \widehat A = 50^\circ \)
\(\begin{array}{l}\frac{{BC}}{{DF}} = \frac{{10}}{8} = \frac{5}{4}\\ = > \frac{{AB}}{{DE}} = \frac{5}{4} \Leftrightarrow \frac{8}{{DE}} = \frac{5}{4} \Rightarrow DE = 6,4\end{array}\)
Mục 1 của chương trình Toán 8 thường tập trung vào việc ôn tập và hệ thống hóa các kiến thức cơ bản về đa thức, phân thức đại số. Việc nắm vững kiến thức này là nền tảng quan trọng để giải quyết các bài tập phức tạp hơn trong chương trình.
Mục 1 thường bao gồm các nội dung sau:
Bài 1: Thực hiện các phép tính sau:
Giải:
Bài 2: Phân tích các đa thức sau thành nhân tử:
Giải:
Bài 3: Rút gọn các biểu thức sau:
Giải:
Để học Toán 8 hiệu quả, các em nên:
Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin giải quyết các bài tập trong mục 1 trang 48, 49, 50 SGK Toán 8. Chúc các em học tập tốt và đạt kết quả cao!