Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 của giaitoan.edu.vn. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Ở bài viết này, chúng ta sẽ cùng nhau đi sâu vào giải chi tiết các bài tập trong mục 2 trang 8, 9, 10 sách giáo khoa Toán 8. Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Hàm số
Ở nam giới trưởng thành, chiều cao H (cm) liên hệ với chiều dài xương chày t (cm) theo công thức \(H\left( t \right) = 2,4t + 78,7\) trong khi ở nữ giới trưởng thành công thức là \(H\left( t \right) = 2,4t + 74,8\). Tính chiều cao của một người đàn ông và một người phụ nữ, biết chiều dài xương chày của họ lần lượt là 37,5 cm và 36cm
Phương pháp giải:
Để tìm được chiều cao của một người đàn ông và một người phụ nữ, biết chiều dài xương chày của họ lần lượt là 37,5 cm và 36cm thì ta thay \(t = 37,5\) vào công thức tính chiều cao của nam giới trưởng thành và thay \(t = 36\) vào công thức tính chiều cao của nữ giới trưởng thành.
Lời giải chi tiết:
Chiều cao của người đàn ông có chiều dài xương chày là 37,5 cm là: \(H\left( {37,5} \right) = 2,4.37,5 + 78,7 = 168,7\left( {cm} \right)\)
Chiều cao của người phụ nữ có chiều dài xương chày là 36 cm là:
\(H\left( {36} \right) = 2,4.36 + 74,8 = 161,1\left( {cm} \right)\)
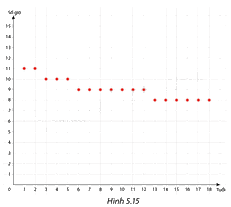
Thời gian ngủ tối thiểu cần thiết hằng ngày h (giờ) của mỗi người là một hàm số phụ thuộc vào độ tuổi t (năm). Hình 5.15. là đồ thị của hàm số đó.
Hãy cho biết trẻ em 6 tuổi, 12 tuổi, 14 tuổi được khuyến nghị ngủ tối thiểu bao nhiêu giờ mỗi ngày?
Phương pháp giải:
Dựa vào cách xác định tọa độ điểm trong mặt phẳng tọa độ để xác định trẻ em 6 tuổi, 12 tuổi, 14 tuổi được khuyến nghị ngủ tối thiểu bao nhiêu giờ mỗi ngày.
Lời giải chi tiết:
Thời gian ngủ tối thiểu của trẻ em 6 tuổi là: 10 giờ
Thời gian ngủ tối thiểu của trẻ em 12 tuổi là: 9 giờ
Thời gian ngủ tối thiểu của trẻ em 14 tuổi là: 8 giờ.
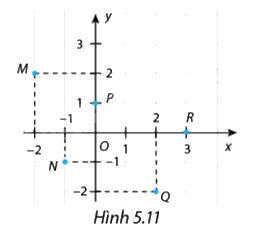
Cho hàm số \(y = f\left( x \right)\) có đồ thị gồm năm điểm \(M,N,P,Q,R\) như Hình 5.11.
a) Tìm \(f\left( { - 2} \right),f\left( 2 \right)\)
b) Lập bảng giá trị của hàm số đã cho.
Phương pháp giải:
Với mỗi giá trị y thì có một giá trị x tương ứng. Dựa vào cách xác định tọa độ trong mặt phẳng tọa độ để xác định \(f\left( { - 2} \right),f\left( 2 \right)\) sau đó lập bảng giá trị.
Lời giải chi tiết:
a) Quan sát Hình 5.11 ta xác định được \(y = f\left( { - 2} \right) = 2\) và \(y = f\left( 2 \right) = - 2\)
b) Ta có tọa độ các điểm \(M,N,P,Q,R\) là: \(M\left( { - 2;2} \right),N\left( { - 1;1} \right),P\left( {0;1} \right),Q\left( {2; - 2} \right),R\left( {3;0} \right)\)
Từ đó ta lập được bảng giá trị sau:

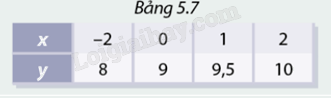
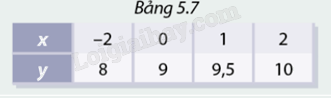
Hàm số \(y = f\left( x \right)\) được cho bởi bảng 5.7.
a) Viết tập hợp các cặp giá trị tương ứng của \(x\) và \(y\).
b) Vẽ một hệ trục tọa độ \(Oxy\) và đánh dấu các điểm có tọa độ là các cặp số trên.
Phương pháp giải:
Viết tập hợp các cặp giá trị tương ứng của \(x\) và \(y\). Sau đó vẽ lên hệ trục tọa độ \(Oxy\).
Lời giải chi tiết:
a) Tập hợp các cặp giá trị tương ứng của \(x\) và \(y\) là: \(A = \left( { - 2;8} \right),B = \left( {0;9} \right),C = \left( {1;9,5} \right),D = \left( {2;10} \right)\).
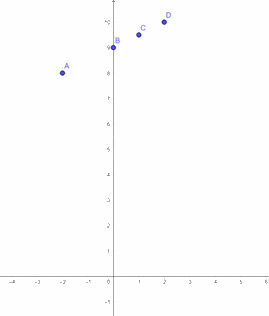
b) Vẽ hệ trục tọa độ \(Oxy\)
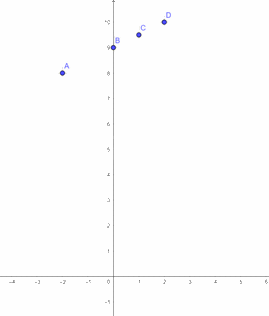
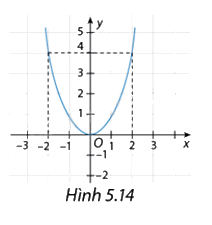
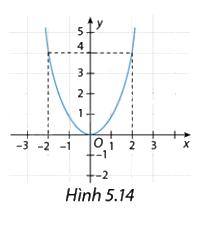
Hình 5.14 cho biết đồ thị của hàm số \(y = f\left( x \right)\). Tìm trên đồ thị của hàm số những điểm có tung độ bằng 4. Điểm \(\left( {1;3} \right)\) có thuộc đồ thị hàm số không?
Phương pháp giải:
Dựa vào cách xác định tọa độ điểm trên mặt phẳng tọa độ để xác định những điểm có tung độ bằng 4 và điểm \(\left( {1;3} \right)\) có thuộc đồ thị hàm số không.
Lời giải chi tiết:
Những điểm có tung độ bằng 4 là: \(\left( {2;4} \right),\left( { - 2;4} \right)\).
Điểm \(\left( {1;3} \right)\) không thuộc đồ thị hàm số.
Hàm số \(y = f\left( x \right)\) được cho bởi bảng 5.7.
a) Viết tập hợp các cặp giá trị tương ứng của \(x\) và \(y\).
b) Vẽ một hệ trục tọa độ \(Oxy\) và đánh dấu các điểm có tọa độ là các cặp số trên.
Phương pháp giải:
Viết tập hợp các cặp giá trị tương ứng của \(x\) và \(y\). Sau đó vẽ lên hệ trục tọa độ \(Oxy\).
Lời giải chi tiết:
a) Tập hợp các cặp giá trị tương ứng của \(x\) và \(y\) là: \(A = \left( { - 2;8} \right),B = \left( {0;9} \right),C = \left( {1;9,5} \right),D = \left( {2;10} \right)\).
b) Vẽ hệ trục tọa độ \(Oxy\)
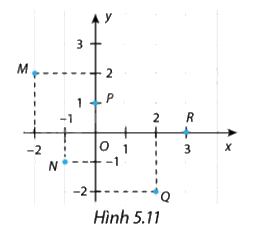
Cho hàm số \(y = f\left( x \right)\) có đồ thị gồm năm điểm \(M,N,P,Q,R\) như Hình 5.11.
a) Tìm \(f\left( { - 2} \right),f\left( 2 \right)\)
b) Lập bảng giá trị của hàm số đã cho.
Phương pháp giải:
Với mỗi giá trị y thì có một giá trị x tương ứng. Dựa vào cách xác định tọa độ trong mặt phẳng tọa độ để xác định \(f\left( { - 2} \right),f\left( 2 \right)\) sau đó lập bảng giá trị.
Lời giải chi tiết:
a) Quan sát Hình 5.11 ta xác định được \(y = f\left( { - 2} \right) = 2\) và \(y = f\left( 2 \right) = - 2\)
b) Ta có tọa độ các điểm \(M,N,P,Q,R\) là: \(M\left( { - 2;2} \right),N\left( { - 1;1} \right),P\left( {0;1} \right),Q\left( {2; - 2} \right),R\left( {3;0} \right)\)
Từ đó ta lập được bảng giá trị sau:

Hình 5.14 cho biết đồ thị của hàm số \(y = f\left( x \right)\). Tìm trên đồ thị của hàm số những điểm có tung độ bằng 4. Điểm \(\left( {1;3} \right)\) có thuộc đồ thị hàm số không?
Phương pháp giải:
Dựa vào cách xác định tọa độ điểm trên mặt phẳng tọa độ để xác định những điểm có tung độ bằng 4 và điểm \(\left( {1;3} \right)\) có thuộc đồ thị hàm số không.
Lời giải chi tiết:
Những điểm có tung độ bằng 4 là: \(\left( {2;4} \right),\left( { - 2;4} \right)\).
Điểm \(\left( {1;3} \right)\) không thuộc đồ thị hàm số.
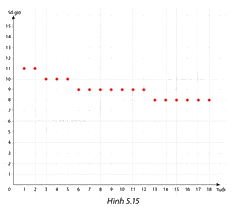
Thời gian ngủ tối thiểu cần thiết hằng ngày h (giờ) của mỗi người là một hàm số phụ thuộc vào độ tuổi t (năm). Hình 5.15. là đồ thị của hàm số đó.
Hãy cho biết trẻ em 6 tuổi, 12 tuổi, 14 tuổi được khuyến nghị ngủ tối thiểu bao nhiêu giờ mỗi ngày?
Phương pháp giải:
Dựa vào cách xác định tọa độ điểm trong mặt phẳng tọa độ để xác định trẻ em 6 tuổi, 12 tuổi, 14 tuổi được khuyến nghị ngủ tối thiểu bao nhiêu giờ mỗi ngày.
Lời giải chi tiết:
Thời gian ngủ tối thiểu của trẻ em 6 tuổi là: 10 giờ
Thời gian ngủ tối thiểu của trẻ em 12 tuổi là: 9 giờ
Thời gian ngủ tối thiểu của trẻ em 14 tuổi là: 8 giờ.
Ở nam giới trưởng thành, chiều cao H (cm) liên hệ với chiều dài xương chày t (cm) theo công thức \(H\left( t \right) = 2,4t + 78,7\) trong khi ở nữ giới trưởng thành công thức là \(H\left( t \right) = 2,4t + 74,8\). Tính chiều cao của một người đàn ông và một người phụ nữ, biết chiều dài xương chày của họ lần lượt là 37,5 cm và 36cm
Phương pháp giải:
Để tìm được chiều cao của một người đàn ông và một người phụ nữ, biết chiều dài xương chày của họ lần lượt là 37,5 cm và 36cm thì ta thay \(t = 37,5\) vào công thức tính chiều cao của nam giới trưởng thành và thay \(t = 36\) vào công thức tính chiều cao của nữ giới trưởng thành.
Lời giải chi tiết:
Chiều cao của người đàn ông có chiều dài xương chày là 37,5 cm là: \(H\left( {37,5} \right) = 2,4.37,5 + 78,7 = 168,7\left( {cm} \right)\)
Chiều cao của người phụ nữ có chiều dài xương chày là 36 cm là:
\(H\left( {36} \right) = 2,4.36 + 74,8 = 161,1\left( {cm} \right)\)
Mục 2 của chương trình Toán 8 thường tập trung vào các kiến thức cơ bản về đa thức, các phép toán trên đa thức, và các ứng dụng của chúng. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Mục 2 thường bao gồm các nội dung sau:
Trang 8 thường chứa các bài tập về nhận biết đa thức, xác định bậc của đa thức, và tìm hệ số của đa thức. Ví dụ:
Bài 1: Tìm bậc của đa thức P(x, y) = 3x2y3 + 5xy2 - 2x + 1.
Giải: Bậc của đa thức P(x, y) là 5 (tổng số mũ của x và y trong mỗi hạng tử).
Trang 9 thường chứa các bài tập về thực hiện các phép cộng, trừ đa thức. Ví dụ:
Bài 2: Thực hiện phép cộng hai đa thức sau: A(x) = 2x2 - 3x + 1 và B(x) = -x2 + 5x - 2.
Giải: A(x) + B(x) = (2x2 - 3x + 1) + (-x2 + 5x - 2) = x2 + 2x - 1.
Trang 10 thường chứa các bài tập về thực hiện phép nhân đa thức. Ví dụ:
Bài 3: Thực hiện phép nhân hai đa thức sau: (x + 2)(x - 3).
Giải: (x + 2)(x - 3) = x(x - 3) + 2(x - 3) = x2 - 3x + 2x - 6 = x2 - x - 6.
| Công thức | Mô tả |
|---|---|
| (a + b)2 = a2 + 2ab + b2 | Bình phương của một tổng |
| (a - b)2 = a2 - 2ab + b2 | Bình phương của một hiệu |
| a2 - b2 = (a + b)(a - b) | Hiệu hai bình phương |
Hy vọng với những giải thích chi tiết và hướng dẫn cụ thể trên đây, các em sẽ tự tin hơn khi giải các bài tập trong mục 2 trang 8, 9, 10 SGK Toán 8. Chúc các em học tốt!