Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong sách giáo khoa Toán 8. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài toán phức tạp.
Với mục tiêu hỗ trợ học sinh học tập hiệu quả, chúng tôi đã biên soạn bộ giải đáp án trang 96, 97 SGK Toán 8 một cách cẩn thận và đầy đủ.
Hãy cùng khám phá và chinh phục những bài toán Toán 8 một cách tự tin!
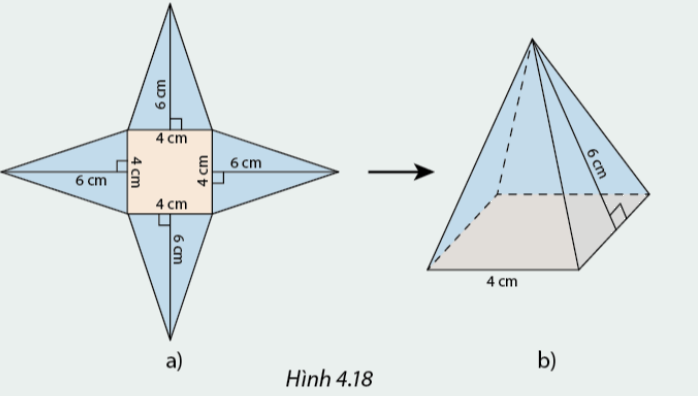
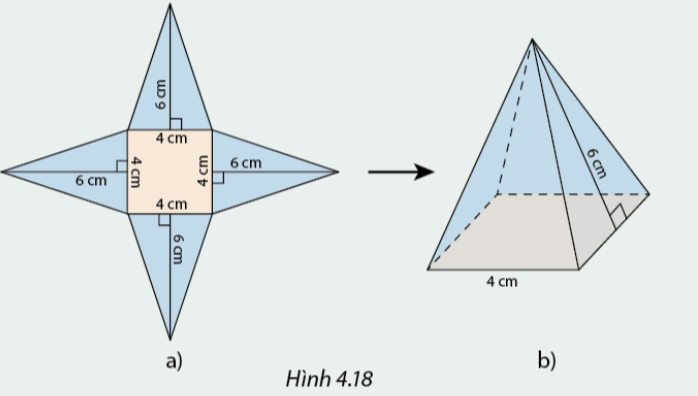
Từ miếng bìa ở Hình 4.18a có thể gấp được hình chop tứ giác đều ở Hình 4.18b.
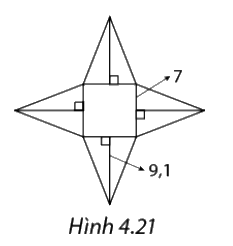
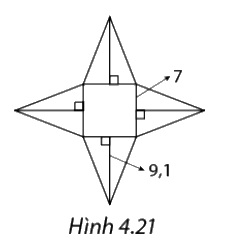
Tính diện tích xung quanh của hình chóp tứ giác đều có hình khai triển như Hình 4.21.
Phương pháp giải:
Áp dụng công thức tính diện tích xung quanh của hình chóp tứ giác đều:
\({S_{xq}} = p.d\)
Với \(p\) là nửa chu vi đáy và \(d\) là đường cao của mặt bên kẻ từ đỉnh của hình chóp đó.
Lời giải chi tiết:
Diện tích xung quanh của hình chóp tứ giác đều là:
\({S_{xq}} = p.d = \left( {7 + 7} \right).9,1 = 127,4\)
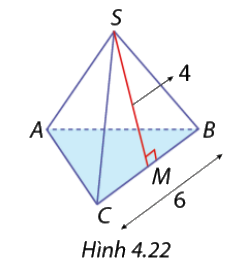
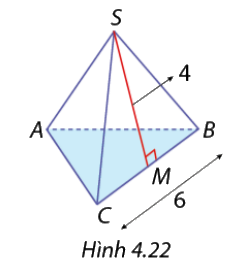
Tính diện tích xung quanh của hình chóp tam giác đều trong Hình 4.22.
Phương pháp giải:
Áp dụng công thức tính diện tích xung quanh của hình chóp tam giác đều:
\({S_{xq}} = p.d\)
Với \(p\) là nửa chu vi đáy và \(d\) là đường cao của mặt bên kẻ từ đỉnh của hình chóp đó.
Lời giải chi tiết:
Diện tích xung quanh của hình chóp tam giác đều là:
\({S_{xq}} = p.d = \left( {\frac{{6 + 6 + 6}}{2}} \right).4 = 36\)
Từ miếng bìa ở Hình 4.18a có thể gấp được hình chop tứ giác đều ở Hình 4.18b.
a) Tính tổng diện tích các mặt bên của hình chóp.
b) So sánh kết quả ở câu a với tích của nửa chu vi đáy và đường cao của mặt bên kẻ từ đỉnh của hình chóp.
Phương pháp giải:
Áp dụng công thức tính diện tích của hình tam giác cân để tính diện tích các mặt bên của hình chóp.
Lời giải chi tiết:
a) Tổng diện tích các mặt bên của hình chóp là:
\(S = \left( {\frac{1}{2}.6.4} \right).4 = 48cm\)
b) Tích của nửa chu vi đáy và đường cao của mặt bên kẻ từ đỉnh của chóp là:
\(\left( {\frac{{4.4}}{2}} \right).6 = 48cm\)
Ta thấy tổng diện tích các mặt bên của hình chóp bằng tích của nửa chu vi đáy với đường cao của mặt bên kẻ từ đỉnh của hình chóp.
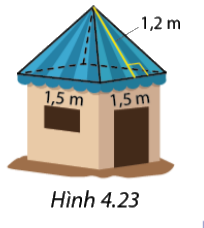
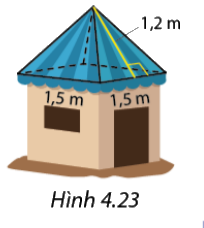
Mái của một chòi trên bãi biển có dạng hình chóp tứ giác đều như Hình 4.23. Tính diện tích vải bạt cần dùng để phủ mái chòi, biết rằng người ta chỉ dùng một lớp vải bạt (không tính phần viền xung quanh)\
Phương pháp giải:
Áp dụng công thức tính diện tích xung quanh của hình chóp tứ giác đều:
\({S_{xq}} = p.d\)
Với \(p\) là nửa chu vi đáy và \(d\) là đường cao của mặt bên kẻ từ đỉnh của hình chóp đó.
Lời giải chi tiết:
Diện tích vải bạt cần dùng để phủ mái chòi là:
\({S_{xq}} = \left( {1,5 + 1,5} \right).1,2 = 3,6{m^2}\)
Từ miếng bìa ở Hình 4.18a có thể gấp được hình chop tứ giác đều ở Hình 4.18b.
a) Tính tổng diện tích các mặt bên của hình chóp.
b) So sánh kết quả ở câu a với tích của nửa chu vi đáy và đường cao của mặt bên kẻ từ đỉnh của hình chóp.
Phương pháp giải:
Áp dụng công thức tính diện tích của hình tam giác cân để tính diện tích các mặt bên của hình chóp.
Lời giải chi tiết:
a) Tổng diện tích các mặt bên của hình chóp là:
\(S = \left( {\frac{1}{2}.6.4} \right).4 = 48cm\)
b) Tích của nửa chu vi đáy và đường cao của mặt bên kẻ từ đỉnh của chóp là:
\(\left( {\frac{{4.4}}{2}} \right).6 = 48cm\)
Ta thấy tổng diện tích các mặt bên của hình chóp bằng tích của nửa chu vi đáy với đường cao của mặt bên kẻ từ đỉnh của hình chóp.
Tính diện tích xung quanh của hình chóp tứ giác đều có hình khai triển như Hình 4.21.
Phương pháp giải:
Áp dụng công thức tính diện tích xung quanh của hình chóp tứ giác đều:
\({S_{xq}} = p.d\)
Với \(p\) là nửa chu vi đáy và \(d\) là đường cao của mặt bên kẻ từ đỉnh của hình chóp đó.
Lời giải chi tiết:
Diện tích xung quanh của hình chóp tứ giác đều là:
\({S_{xq}} = p.d = \left( {7 + 7} \right).9,1 = 127,4\)
Tính diện tích xung quanh của hình chóp tam giác đều trong Hình 4.22.
Phương pháp giải:
Áp dụng công thức tính diện tích xung quanh của hình chóp tam giác đều:
\({S_{xq}} = p.d\)
Với \(p\) là nửa chu vi đáy và \(d\) là đường cao của mặt bên kẻ từ đỉnh của hình chóp đó.
Lời giải chi tiết:
Diện tích xung quanh của hình chóp tam giác đều là:
\({S_{xq}} = p.d = \left( {\frac{{6 + 6 + 6}}{2}} \right).4 = 36\)
Mái của một chòi trên bãi biển có dạng hình chóp tứ giác đều như Hình 4.23. Tính diện tích vải bạt cần dùng để phủ mái chòi, biết rằng người ta chỉ dùng một lớp vải bạt (không tính phần viền xung quanh)\
Phương pháp giải:
Áp dụng công thức tính diện tích xung quanh của hình chóp tứ giác đều:
\({S_{xq}} = p.d\)
Với \(p\) là nửa chu vi đáy và \(d\) là đường cao của mặt bên kẻ từ đỉnh của hình chóp đó.
Lời giải chi tiết:
Diện tích vải bạt cần dùng để phủ mái chòi là:
\({S_{xq}} = \left( {1,5 + 1,5} \right).1,2 = 3,6{m^2}\)
Chương trình Toán 8 là bước đệm quan trọng để học sinh làm quen với những khái niệm toán học phức tạp hơn ở các lớp trên. Trang 96 và 97 của sách giáo khoa Toán 8 thường chứa các bài tập về các chủ đề như đa thức, phân thức đại số, phương trình bậc nhất một ẩn, và hệ phương trình bậc nhất hai ẩn. Việc nắm vững kiến thức và kỹ năng giải các bài tập này là vô cùng quan trọng để đạt kết quả tốt trong môn Toán.
Bài tập này thường yêu cầu học sinh thực hiện các phép toán với đa thức và phân thức đại số, như cộng, trừ, nhân, chia, và rút gọn. Để giải các bài tập này, học sinh cần nắm vững các quy tắc về phép toán với đa thức và phân thức đại số, cũng như các kỹ năng biến đổi đại số.
Bài tập này yêu cầu học sinh giải các phương trình bậc nhất một ẩn. Để giải các bài tập này, học sinh cần nắm vững các bước giải phương trình bậc nhất một ẩn, như chuyển vế, quy đồng mẫu số, và tìm nghiệm.
Bài tập này yêu cầu học sinh giải các hệ phương trình bậc nhất hai ẩn. Để giải các bài tập này, học sinh có thể sử dụng các phương pháp như phương pháp thế, phương pháp cộng đại số, hoặc phương pháp ma trận.
| Phương pháp | Ưu điểm | Nhược điểm |
|---|---|---|
| Phương pháp thế | Dễ hiểu, dễ áp dụng | Có thể phức tạp nếu hệ số của một ẩn bằng 0 |
| Phương pháp cộng đại số | Thường nhanh hơn phương pháp thế | Đòi hỏi kỹ năng biến đổi đại số tốt |
Để học tập môn Toán 8 hiệu quả, học sinh cần:
Việc giải các bài tập trang 96, 97 SGK Toán 8 là một bước quan trọng trong quá trình học tập môn Toán 8. Hy vọng rằng với những hướng dẫn chi tiết và hữu ích trên đây, các em học sinh sẽ tự tin hơn trong việc giải các bài tập Toán 8 và đạt kết quả tốt trong môn học này. Chúc các em học tập tốt!