Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 của giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho mục 3 trang 72, 73, 74 sách giáo khoa Toán 8. Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán và đạt kết quả tốt trong môn học.
Chúng tôi hiểu rằng việc học Toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic và có ví dụ minh họa cụ thể.
1. Trong Hình 3.55, tầng trên của khay đựng giấy được gắn với tầng dưới bởi hai thanh AD, BC
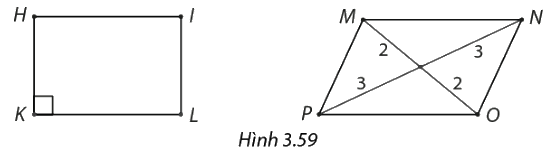
Trong hình 3.59, Hình bình hành nào là hình chữ nhật?
Phương pháp giải:
Sử dụng dhnb hình chữ nhật:
Hình bình hành có một góc vuông là hình chữ nhật.
Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
Lời giải chi tiết:
Hình bình hành HILK có 1 góc vuông nên HILK là hình chữ nhật (dhnb).
Hình bình hành MNPQ có 2 đường chéo không bằng nhau nên không phải hình chữ nhật.
1. Trong Hình 3.57, khi hai bên nắp hộp được mở đều về hai phía, mép AD và BC của hai nắp là hai cạnh bên của một hình thang cân. Góc ADC như thế nào thì ABCD là hình chữ nhật?
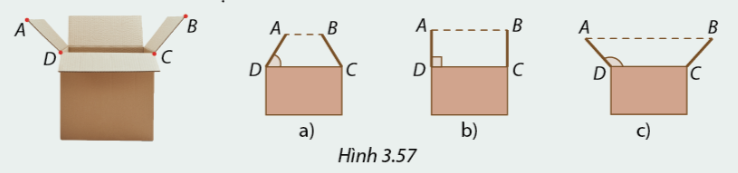
2. Giải thích câu trả lời ở trên của em bằng cách tính các góc của hình thang cân ABCD nếu \(\widehat {ADC} = 90^\circ \).(Hình 3.57b)
Phương pháp giải:
Dựa vào hình vẽ, rút ra kết luận
Giải thích câu trả lời ở trên của em bằng cách tính các góc của hình thang cân ABCD nếu \(\widehat {ADC} = 90^\circ \).(Hình 3.57b)
Lời giải chi tiết:
1. Góc ADC vuông thì ABCD là hình chữ nhật
2. Xét hình thanh cân ABCD có \(\widehat D = \widehat C\) suy ra \(\widehat C = 90^\circ \)
Có \(AB//CD \Rightarrow \widehat A + \widehat D = 180^\circ \) (hai góc trong cùng phía)
\(\widehat A = 180^\circ - \widehat D = 90^\circ \)
Suy ra tứ giác ABCD là hình chữ nhât. (\(\widehat A = \widehat D = \widehat C = 90^\circ .\))
1. Trong hình 3.56, hình bình hành ABCD có đường chéo BD cố định, còn AC có thể thay đổi bằng cách di chuyển điểm C trên tia Dx. Độ dài AC như thế nào so với BD thì ABCD là hình chữ nhật?

2. Dựa vào tính chất và dấu hiệu nhận biết hình thang cân, em hãy giải thích vì sao khi \(AC = BD\) thì hình bình hành ABCD có bốn góc bằng nhau. Tính số đo mỗi góc và cho biết khi đó ABCD là hình gì?
Phương pháp giải:
Dựa vào hình vẽ ở đề bài.
Dựa vào tính chất và dấu hiệu nhận biết hình thang cân, giải thích vì sao khi \(AC = BD\) thì hình bình hành ABCD có bốn góc bằng nhau.
Lời giải chi tiết:
1. Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật:
\(AC = BD\) thì ABCD là hình chữ nhật.
2. Có \(AC = BD\) thì \(\Delta ADC = \Delta DBC\left( {c - c - c} \right)\)
\( \Rightarrow \widehat D = \widehat B\)
Tương tự \( \Rightarrow \Delta DAB = \Delta CAB\left( {c - c - c} \right) \Rightarrow \widehat A = \widehat B\)
Mà hình bình hành ABCD có các góc đối bằng nhau \( \Rightarrow \widehat A = \widehat B = \widehat C = \widehat D\)
Vậy khi \(AC = BD\) thì hình bình hành ABCD có bốn góc bằng nhau.
1. Trong Hình 3.55, tầng trên của khay đựng giấy được gắn với tầng dưới bởi hai thanh AD, BC với \(AB = DC,AD = BC.\) Ta có thể đưa tầng trên của khay ra trước hoặc về sau bằng cách thay đổi góc ADC. Em hãy cho biết:
a) Tứ giác ABCD luôn là hình gì?
b) Khi góc ADC bằng bao nhiêu độ thì ABCD là hình chữ nhật?
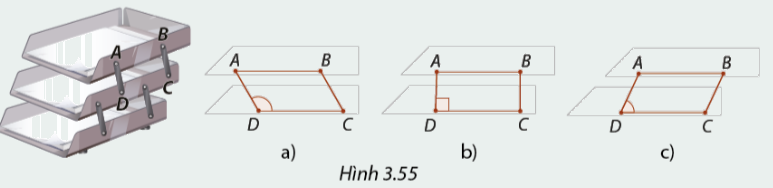
2. Giải thích câu trả lời ở trên của em bằng cách tính các góc hình bình hành ABCD nếu \(\widehat {ADC} = 90^\circ \)(Hình 3.55b).
Phương pháp giải:
1. Sử dụng dhnb hình bình hành, kết hợp với hình vẽ ở đề bài.
2. Tính các góc hình bình hành ABCD nếu \(\widehat {ADC} = 90^\circ \)(Hình 3.55b) và giải thích.
Lời giải chi tiết:
1.
a) Xét tứ giác ABCD có \(AB = DC,AD = BC.\)Vậy tứ giác ABCD là hình bình hành (dhnb).
b) Khi ADC bằng \(90^\circ \) thì hình bình hành ABCD là hình chữ nhật (dhnb).
2. Xét hình bình hành ABCD có \(\widehat {ADC} = \widehat {ABC} = 90^\circ \) (cặp góc đối bằng nhau).
Có \(AB//CD \Rightarrow \widehat {DAB} + \widehat {ACD} = 180^\circ \) (hai góc trong cùng phía)
Suy ra \(\widehat {DAB} = 90^\circ \)
Xét tứ giác ABCD có \(\widehat {ADC} = \widehat {ABC} = \widehat {DAB} = 90^\circ \) suy ra ABCD là hình chữ nhật.
Trong Hình 3.60, mặt ABCD của thùng gỗ được gia cố bằng hai thanh gỗ AC và BD. Chỉ dùng thước đo độ dài, bác thợ mộc có thể khẳng định các góc A, B, C, D của mặt thùng đều vuông. Em hãy cho biết bác đã làm cách nào.

Phương pháp giải:
Sử dụng dhnb hình chữ nhật:
Hình bình hành có một góc vuông là hình chữ nhật.
Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
Lời giải chi tiết:
Đầu tiên dùng thước thẳng đo bốn cạnh AB; BC; CD; AD ta thấy \(AB = CD;AD = BC\) suy ra tứ giác ABCD là hình bình hành (dhnb)
Dùng thước thẳng đo AC; BD ta thấy \(AC = BD\) suy ra ABCD là hình chữ nhật (dhnb).
Vậy 4 góc của thùng bằng nhau và bằng \(90^\circ .\)
Bác thợ mộc có thể khẳng định các góc A, B, C, D của mặt thùng đều vuông
1. Trong Hình 3.55, tầng trên của khay đựng giấy được gắn với tầng dưới bởi hai thanh AD, BC với \(AB = DC,AD = BC.\) Ta có thể đưa tầng trên của khay ra trước hoặc về sau bằng cách thay đổi góc ADC. Em hãy cho biết:
a) Tứ giác ABCD luôn là hình gì?
b) Khi góc ADC bằng bao nhiêu độ thì ABCD là hình chữ nhật?
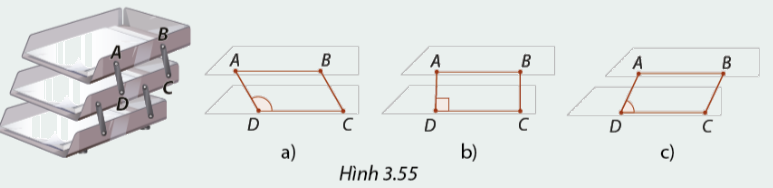
2. Giải thích câu trả lời ở trên của em bằng cách tính các góc hình bình hành ABCD nếu \(\widehat {ADC} = 90^\circ \)(Hình 3.55b).
Phương pháp giải:
1. Sử dụng dhnb hình bình hành, kết hợp với hình vẽ ở đề bài.
2. Tính các góc hình bình hành ABCD nếu \(\widehat {ADC} = 90^\circ \)(Hình 3.55b) và giải thích.
Lời giải chi tiết:
1.
a) Xét tứ giác ABCD có \(AB = DC,AD = BC.\)Vậy tứ giác ABCD là hình bình hành (dhnb).
b) Khi ADC bằng \(90^\circ \) thì hình bình hành ABCD là hình chữ nhật (dhnb).
2. Xét hình bình hành ABCD có \(\widehat {ADC} = \widehat {ABC} = 90^\circ \) (cặp góc đối bằng nhau).
Có \(AB//CD \Rightarrow \widehat {DAB} + \widehat {ACD} = 180^\circ \) (hai góc trong cùng phía)
Suy ra \(\widehat {DAB} = 90^\circ \)
Xét tứ giác ABCD có \(\widehat {ADC} = \widehat {ABC} = \widehat {DAB} = 90^\circ \) suy ra ABCD là hình chữ nhật.
1. Trong hình 3.56, hình bình hành ABCD có đường chéo BD cố định, còn AC có thể thay đổi bằng cách di chuyển điểm C trên tia Dx. Độ dài AC như thế nào so với BD thì ABCD là hình chữ nhật?

2. Dựa vào tính chất và dấu hiệu nhận biết hình thang cân, em hãy giải thích vì sao khi \(AC = BD\) thì hình bình hành ABCD có bốn góc bằng nhau. Tính số đo mỗi góc và cho biết khi đó ABCD là hình gì?
Phương pháp giải:
Dựa vào hình vẽ ở đề bài.
Dựa vào tính chất và dấu hiệu nhận biết hình thang cân, giải thích vì sao khi \(AC = BD\) thì hình bình hành ABCD có bốn góc bằng nhau.
Lời giải chi tiết:
1. Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật:
\(AC = BD\) thì ABCD là hình chữ nhật.
2. Có \(AC = BD\) thì \(\Delta ADC = \Delta DBC\left( {c - c - c} \right)\)
\( \Rightarrow \widehat D = \widehat B\)
Tương tự \( \Rightarrow \Delta DAB = \Delta CAB\left( {c - c - c} \right) \Rightarrow \widehat A = \widehat B\)
Mà hình bình hành ABCD có các góc đối bằng nhau \( \Rightarrow \widehat A = \widehat B = \widehat C = \widehat D\)
Vậy khi \(AC = BD\) thì hình bình hành ABCD có bốn góc bằng nhau.
1. Trong Hình 3.57, khi hai bên nắp hộp được mở đều về hai phía, mép AD và BC của hai nắp là hai cạnh bên của một hình thang cân. Góc ADC như thế nào thì ABCD là hình chữ nhật?
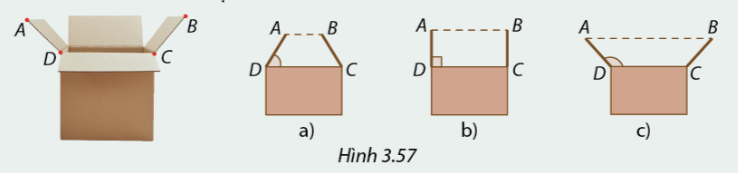
2. Giải thích câu trả lời ở trên của em bằng cách tính các góc của hình thang cân ABCD nếu \(\widehat {ADC} = 90^\circ \).(Hình 3.57b)
Phương pháp giải:
Dựa vào hình vẽ, rút ra kết luận
Giải thích câu trả lời ở trên của em bằng cách tính các góc của hình thang cân ABCD nếu \(\widehat {ADC} = 90^\circ \).(Hình 3.57b)
Lời giải chi tiết:
1. Góc ADC vuông thì ABCD là hình chữ nhật
2. Xét hình thanh cân ABCD có \(\widehat D = \widehat C\) suy ra \(\widehat C = 90^\circ \)
Có \(AB//CD \Rightarrow \widehat A + \widehat D = 180^\circ \) (hai góc trong cùng phía)
\(\widehat A = 180^\circ - \widehat D = 90^\circ \)
Suy ra tứ giác ABCD là hình chữ nhât. (\(\widehat A = \widehat D = \widehat C = 90^\circ .\))
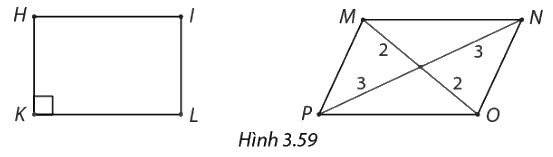
Trong hình 3.59, Hình bình hành nào là hình chữ nhật?
Phương pháp giải:
Sử dụng dhnb hình chữ nhật:
Hình bình hành có một góc vuông là hình chữ nhật.
Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
Lời giải chi tiết:
Hình bình hành HILK có 1 góc vuông nên HILK là hình chữ nhật (dhnb).
Hình bình hành MNPQ có 2 đường chéo không bằng nhau nên không phải hình chữ nhật.
Trong Hình 3.60, mặt ABCD của thùng gỗ được gia cố bằng hai thanh gỗ AC và BD. Chỉ dùng thước đo độ dài, bác thợ mộc có thể khẳng định các góc A, B, C, D của mặt thùng đều vuông. Em hãy cho biết bác đã làm cách nào.

Phương pháp giải:
Sử dụng dhnb hình chữ nhật:
Hình bình hành có một góc vuông là hình chữ nhật.
Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
Lời giải chi tiết:
Đầu tiên dùng thước thẳng đo bốn cạnh AB; BC; CD; AD ta thấy \(AB = CD;AD = BC\) suy ra tứ giác ABCD là hình bình hành (dhnb)
Dùng thước thẳng đo AC; BD ta thấy \(AC = BD\) suy ra ABCD là hình chữ nhật (dhnb).
Vậy 4 góc của thùng bằng nhau và bằng \(90^\circ .\)
Bác thợ mộc có thể khẳng định các góc A, B, C, D của mặt thùng đều vuông
Mục 3 trong sách giáo khoa Toán 8 thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững các khái niệm và định lý liên quan. Việc giải các bài tập trong mục này không chỉ giúp các em củng cố kiến thức mà còn rèn luyện kỹ năng giải toán, tư duy logic và khả năng áp dụng kiến thức vào thực tế.
Để hiểu rõ hơn về nội dung của Mục 3, chúng ta cần xem xét các bài tập cụ thể được đề cập trong sách giáo khoa. Thông thường, các bài tập này sẽ bao gồm:
Dưới đây là hướng dẫn giải chi tiết cho một số bài tập tiêu biểu trong Mục 3 trang 72, 73, 74 SGK Toán 8:
Đề bài: Cho tam giác ABC vuông tại A, có AB = 3cm, AC = 4cm. Tính độ dài cạnh BC.
Lời giải:
Kết luận: Độ dài cạnh BC là 5cm.
Đề bài: Cho hai đường thẳng song song a và b, bị cắt bởi đường thẳng c. Chứng minh rằng các góc so le trong bằng nhau.
Lời giải:
(Chứng minh chi tiết dựa trên các định lý về góc so le trong và góc đồng vị)
Để học tốt môn Toán 8, các em có thể tham khảo một số mẹo sau:
Kiến thức trong Mục 3 có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, chẳng hạn như:
Hy vọng rằng với hướng dẫn chi tiết và các mẹo học tập trên, các em sẽ tự tin giải quyết các bài tập trong Mục 3 trang 72, 73, 74 SGK Toán 8. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!