Chào mừng các em học sinh đến với bài giải chi tiết bài 3.42 trang 90 SGK Toán 8. Tại giaitoan.edu.vn, chúng tôi cung cấp phương pháp giải bài tập Toán 8 một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Bài 3.42 thuộc chương trình Toán 8, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế. Chúng tôi sẽ hướng dẫn các em từng bước, từ việc phân tích đề bài đến việc đưa ra lời giải chính xác.
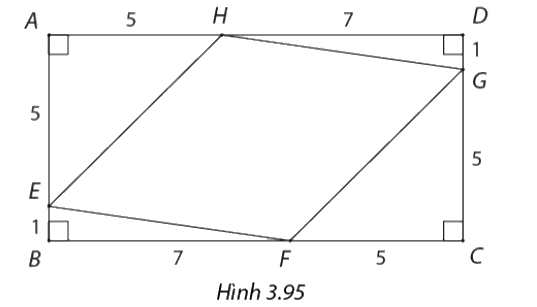
Trong Hình 3.95,
Đề bài
Trong Hình 3.95, \(ABCD\) là hình chữ nhật, \(E,F,G,H\) lần lượt là các điểm nằm trên các cạnh \(AB,BC,CD,AD\) và \(BE = DG = 1cm,BF = DH = 7cm,AE = AH = CF = CG = 5cm\).
a) Tính độ dài các cạnh của tứ giác \(EFGH\).
b) Chứng minh rằng \(HF\) vuông góc với \(EG\).
Phương pháp giải - Xem chi tiết
Dựa vào đinh lí Pythagore để tính các cạnh.
Lời giải chi tiết
a) Độ dài của cạnh \(HE\) là: \(HE = \sqrt {{5^2} + {5^2}} = 5\sqrt 2 \)
Độ dài của cạnh \(EF\) là: \(EF = \sqrt {{7^2} + {1^2}} = 5\sqrt 2 \)
Độ dài của cạnh \(FG\) là: \(FG = \sqrt {{5^2} + {5^2}} = 5\sqrt 2 \)
Độ dài của cạnh \(GH\) là: \(GH = \sqrt {{7^2} + {1^2}} = 5\sqrt 2 \)
b) Tứ giác \(EFGH\) có bốn cạnh \(EF = FG = GH = HE = 5\sqrt 2 \) và không có góc vuông.
→ Tứ giác \(EFGH\) là hình thoi
Mà \(HF\) và \(EG\) là hai đường chéo của hình thoi \(EFGH\)
→ \(HF \bot EG\)
Bài 3.42 trang 90 SGK Toán 8 là một bài tập quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về các dạng toán đã học. Bài tập này thường liên quan đến việc áp dụng các định lý, tính chất hình học hoặc đại số để giải quyết các vấn đề cụ thể.
Trước khi bắt đầu giải bài tập, điều quan trọng nhất là phải đọc kỹ đề bài và hiểu rõ yêu cầu. Xác định các dữ kiện đã cho và những điều cần tìm. Vẽ hình minh họa (nếu cần thiết) để giúp hình dung rõ hơn về bài toán.
Tùy thuộc vào nội dung cụ thể của bài tập, phương pháp giải có thể khác nhau. Tuy nhiên, một số phương pháp thường được sử dụng bao gồm:
(Nội dung lời giải chi tiết sẽ được trình bày tại đây, bao gồm các bước giải, giải thích rõ ràng và chính xác. Ví dụ, nếu bài toán là chứng minh một tính chất hình học, lời giải sẽ trình bày các bước chứng minh một cách logic và khoa học. Nếu bài toán là giải phương trình, lời giải sẽ trình bày các bước biến đổi phương trình để tìm ra nghiệm.)
Để giúp các em hiểu rõ hơn về cách giải bài tập, chúng ta sẽ xem xét một ví dụ minh họa cụ thể. (Ví dụ sẽ được trình bày chi tiết, bao gồm đề bài, lời giải và giải thích.)
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, các em có thể tự giải các bài tập tương tự sau:
Bài 3.42 trang 90 SGK Toán 8 là một bài tập quan trọng, giúp các em rèn luyện kỹ năng giải toán và củng cố kiến thức đã học. Hy vọng với hướng dẫn chi tiết và dễ hiểu này, các em sẽ tự tin hơn trong việc giải quyết bài tập và đạt kết quả tốt trong môn Toán.
Để hiểu sâu hơn về các kiến thức liên quan đến bài 3.42 trang 90 SGK Toán 8, các em có thể tham khảo thêm các tài liệu sau:
Để học tốt môn Toán 8, các em cần:
Chúc các em học tốt môn Toán 8!