Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8. Mục 1 trang 93 SGK Toán 8 là một phần quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức và kỹ năng giải bài tập.
Chúng tôi sẽ giúp bạn hiểu rõ hơn về nội dung bài học, cách giải các bài tập và áp dụng kiến thức vào thực tế.
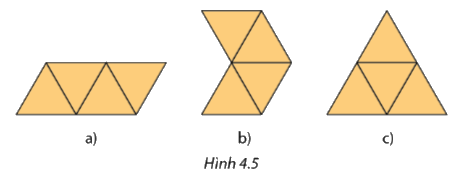
Trong Hình 4.5, hình nào là hình khai triển của hình chóp tam giác đều?
Trong Hình 4.5, hình nào là hình khai triển của hình chóp tam giác đều?
Phương pháp giải:
Hình chóp tam giác đều là hình có các mặt bên là các tam giác cân bằng nhau
Một đỉnh chung và có mặt đáy là tam giác đều.
Lời giải chi tiết:
Hình c) là hình khai triển của hình chóp tam giác đều.
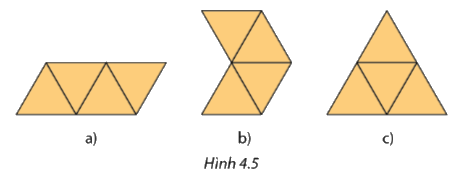
Trong Hình 4.5, hình nào là hình khai triển của hình chóp tam giác đều?
Phương pháp giải:
Hình chóp tam giác đều là hình có các mặt bên là các tam giác cân bằng nhau
Một đỉnh chung và có mặt đáy là tam giác đều.
Lời giải chi tiết:
Hình c) là hình khai triển của hình chóp tam giác đều.
Mục 1 trang 93 SGK Toán 8 thường xoay quanh các chủ đề về hình học, cụ thể là các kiến thức liên quan đến tứ giác. Để giải quyết các bài tập trong mục này, học sinh cần nắm vững các định nghĩa, tính chất của các loại tứ giác đặc biệt như hình bình hành, hình chữ nhật, hình thoi, hình vuông. Việc hiểu rõ các dấu hiệu nhận biết cũng vô cùng quan trọng.
Mục 1 trang 93 thường bao gồm các bài tập vận dụng kiến thức về:
Cho tứ giác ABCD có AB = CD, AD = BC. Chứng minh tứ giác ABCD là hình bình hành.
Hướng dẫn giải:
Cho hình chữ nhật ABCD có AB = 8cm, BC = 6cm. Tính độ dài đường chéo AC.
Hướng dẫn giải:
Áp dụng định lý Pitago vào tam giác vuông ABC, ta có:
AC2 = AB2 + BC2 = 82 + 62 = 64 + 36 = 100
Suy ra AC = √100 = 10cm
Để giải các bài tập về tứ giác nhanh chóng và hiệu quả, bạn nên:
Kiến thức về tứ giác có ứng dụng rộng rãi trong thực tế, ví dụ như:
Hy vọng với hướng dẫn chi tiết này, bạn đã hiểu rõ hơn về cách giải các bài tập trong Mục 1 trang 93 SGK Toán 8. Hãy luyện tập thường xuyên để nắm vững kiến thức và đạt kết quả tốt nhất trong môn Toán.