Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 của giaitoan.edu.vn. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Với mục tiêu hỗ trợ tối đa cho các em trong quá trình học tập, chúng tôi đã biên soạn bộ giải chi tiết các bài tập trong SGK Toán 8, bắt đầu từ mục 1 trang 17, 18, 19.
Hãy cùng khám phá lời giải và phương pháp giải bài tập một cách dễ dàng và hiệu quả nhất!
a) Vẽ đồ thị hai hàm số
Bạn Trọng tham gia cuộc thi trực tuyến “Tinh hoa Việt Nam” về những nét đặc sắc trong văn hóa nước ta. Khi mới tạo tài khoản dự thi, Trọng được tặng 50 điểm tích lũy. Mỗi khi trả lời đúng một câu hỏi, số điểm tích lũy T của Trọng được tăng theeo 5 điểm. Nếu trả lời sai câu hỏi thì không bị trừ điểm.
a) Tìm công thức biểu diễn hàm số T theo số câu hỏi n mà Trọng trả lời đúng
b) Tìm số điểm tích lũy của Trọng, biết rẳng Trọng đã trả lời đúng 18 câu hỏi.
Phương pháp giải:
Gọi số câu hỏi mà Trọng trả lời được là \(n\). Dựa vào các dữ liệu mà đề bài cho về mối quan hệ giữa các câu hỏi và điểm tích lũy, ta biểu diễn được hàm số T theo số câu hỏi \(n\) mà Trọng trả lời đúng, sau đó tìm số điểm tích lũy của Trọng khi trả lời được 18 câu hỏi.
Lời giải chi tiết:
a) Gọi số câu hỏi mà Trọng trả lời được là \(n\). Thì công thức biểu diễn hàm số T theo số câu hỏi \(n\) mà Trọng trả lời đúng là: \(T = 50 + 5n\)
b) Số điểm tích lũy của Trọng khi trả lời đúng 18 câu hỏi là: \(T = 50 + 5.8 = 90\) (điểm)
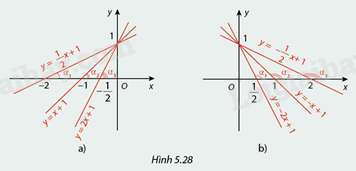
a) Hình 5.28a biểu diễn đồ thị của các hàm số bậc nhất với hệ số a > 0:
\(y = \frac{1}{2}x + 1\)
\(y = x + 1\)
\(y = 2x + 1\)
So sánh các góc \({\alpha _1},{\alpha _2},{\alpha _3}\) và so sánh các hệ số \(a\) tương ứng của các hàm số trên rồi rút ra nhận xét.
b) Hình 5.28b biểu diễn đồ thị của các hàm số bậc nhất với hệ số a < 0:
\(y = - 2x + 1\)
\(y = - x + 1\)
\(y = - \frac{1}{2}x + 1\)
So sánh các góc \({\alpha _1},{\alpha _2},{\alpha _3}\) và so sánh các hệ số \(a\) tương ứng của các hàm số trên rồi rút ra nhận xét.
Phương pháp giải:
Quan sát Hình 5.28 và các hàm số ta có thể xác định được các hệ số \(a\), sau đó so sánh hệ số \(a\) của các hàm số đó và so sánh các góc \({\alpha _1},{\alpha _2},{\alpha _3}\).
Lời giải chi tiết:
a) Quan sát hình 5.28a ta thấy các góc \({\alpha _1} < {\alpha _2} < {\alpha _3}\)
Hàm số \(y = \frac{1}{2}x + 1\) có hệ số \({a_1} = \frac{1}{2}\)
Hàm số \(y = x + 1\) có hệ số \({a_2} = 1\)
Hàm số \(y = 2x + 1\) có hệ số \({a_3} = 2\)
Vậy qua đó ta được \(0 < {a_1} < {a_2} < {a_3}\)
b) Quan sát hình 5.28b ta thấy các góc \({\alpha _1} > {\alpha _2} > {\alpha _3}\)
Hàm số \(y = - 2x + 1\) có hệ số \({a_1} = - 2\)
Hàm số \(y = - x + 1\) có hệ số \({a_2} = - 1\)
Hàm số \(y = - \frac{1}{2}x + 1\) có hệ số \({a_3} = - \frac{1}{2}\)
Vậy qua đó ta được \({a_1} < {a_2} < {a_3} < 0\)
Cho hàm số bậc nhất \(y = ax\) có đồ thị là đường thẳng d như Hình 5.29. Tìm hệ số góc a.
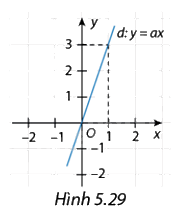
Phương pháp giải:
Hệ số \(a\) được gọi là hệ số góc của đường thẳng \(y = ax + b\) hay là hệ số góc của đồ thị hàm số \(y = ax + b\)\(\left( {a \ne 0} \right)\)
Lời giải chi tiết:
Quan sát hình 5.29, ta thấy hàm số bậc nhất \(y = ax\) có hệ số góc \(a = \frac{y}{x} = \frac{3}{1} = 3\).
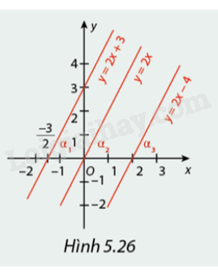
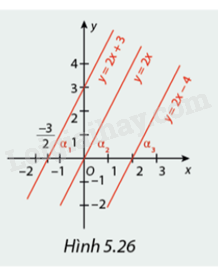
Hình 5.26 biểu diễn đồ thị của các hàm số bậc nhất \(y = 2x + 3,y = 2x\) và \(y = 2x - 4\). So sánh hệ số a của các hàm số trên. So sánh các góc \({\alpha _1},{\alpha _2},{\alpha _3}\) .
Phương pháp giải:
Quan sát Hình 5.26 và các hàm số ta có thể xác định được các hệ số \(a\), sau đó so sánh hệ số \(a\) của các hàm số đó và so sánh các góc \({\alpha _1},{\alpha _2},{\alpha _3}\).
Lời giải chi tiết:
Hàm số \(y = 2x + 3\) có \(a = 2\)
Hàm số \(y = 2x\) có \(a = 2\)
Hàm số \(y = 2x - 4\) có \(a = 2\)
Từ đó ta thấy các hệ số góc của ba hàm số này bằng nhau.
Các góc \({\alpha _1},{\alpha _2},{\alpha _3}\) bằng nhau.
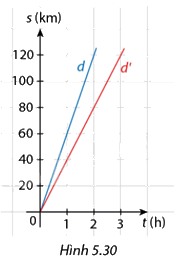
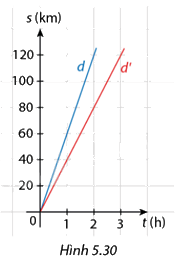
Trong Hình 5.30, các đường thẳng \(d\) và \(d'\) lần lượt chứa đồ thị quãng đường – thời gian của hai ô tô A và B chuyển động đều.
a) Tìm các số thích hợp cho ô trống trong Bảng 5.16.
b) Xác định hệ số góc của mỗi đường thẳng.
c) Tính tốc độ của mỗi xe. Em có nhận xét gì về tốc độ của mỗi xe và hệ số góc của đồ thị quãng đường – thời gian tương ứng?

Phương pháp giải:
Dựa vào cách xác định tọa độ trong mặt phẳng tọa độ học ở bài trước để tìm các số thích hợp cho Bảng 5.16.
Xác định hệ số góc của mỗi đường thẳng bằng cách thay các giá trị \(x,y\) vừa tìm được vào công thức \(y = ax + b\). Sau đó tính tốc độ của mỗi xe dựa vào công thức \(s = v.t\).
Lời giải chi tiết:
a) Quan sát Hình 5.30 ta được Bảng 5.16 như sau: 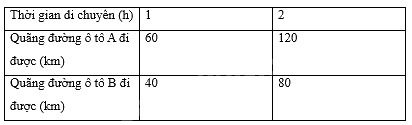
b) Quan sát Hình 5.30 ta thấy cả hai đường thẳng d và d’ đều đi qua gốc tọa độ \(O\left( {0;0} \right)\), vậy cả hai đường thẳng đều có dạng \(y = ax\).
Đường thẳng d đi qua điểm có tọa độ \(\left( {1;60} \right)\) thay vào hàm số \(y = ax\), ta có:
\(\begin{array}{l}60 = a.1\\ = > a = 60\end{array}\)
Vậy hệ số góc của đường thẳng d là \(a = 60\)
Đường thẳng d’ đi qua điểm có tọa độ \(\left( {1;40} \right)\) thay vào hàm số \(y = ax\), ta có:
\(\begin{array}{l}40 = a.1\\ = > a = 40\end{array}\)
Vậy hệ số góc của đường thẳng d’ là \(a = 40\)
c) Tốc độ của xe A là: \(v = \frac{s}{t} = \frac{{60}}{1} = 60\left( {km/h} \right)\)
Tốc độ của xe B là: \(v = \frac{s}{t} = \frac{{40}}{1} = 40\left( {km/h} \right)\)
Ta thấy tốc độ của mỗi xe bằng với hệ số góc của đồ thị quãng đường – thời gian tương ứng.
Hình 5.26 biểu diễn đồ thị của các hàm số bậc nhất \(y = 2x + 3,y = 2x\) và \(y = 2x - 4\). So sánh hệ số a của các hàm số trên. So sánh các góc \({\alpha _1},{\alpha _2},{\alpha _3}\) .
Phương pháp giải:
Quan sát Hình 5.26 và các hàm số ta có thể xác định được các hệ số \(a\), sau đó so sánh hệ số \(a\) của các hàm số đó và so sánh các góc \({\alpha _1},{\alpha _2},{\alpha _3}\).
Lời giải chi tiết:
Hàm số \(y = 2x + 3\) có \(a = 2\)
Hàm số \(y = 2x\) có \(a = 2\)
Hàm số \(y = 2x - 4\) có \(a = 2\)
Từ đó ta thấy các hệ số góc của ba hàm số này bằng nhau.
Các góc \({\alpha _1},{\alpha _2},{\alpha _3}\) bằng nhau.
a) Hình 5.28a biểu diễn đồ thị của các hàm số bậc nhất với hệ số a > 0:
\(y = \frac{1}{2}x + 1\)
\(y = x + 1\)
\(y = 2x + 1\)
So sánh các góc \({\alpha _1},{\alpha _2},{\alpha _3}\) và so sánh các hệ số \(a\) tương ứng của các hàm số trên rồi rút ra nhận xét.
b) Hình 5.28b biểu diễn đồ thị của các hàm số bậc nhất với hệ số a < 0:
\(y = - 2x + 1\)
\(y = - x + 1\)
\(y = - \frac{1}{2}x + 1\)
So sánh các góc \({\alpha _1},{\alpha _2},{\alpha _3}\) và so sánh các hệ số \(a\) tương ứng của các hàm số trên rồi rút ra nhận xét.
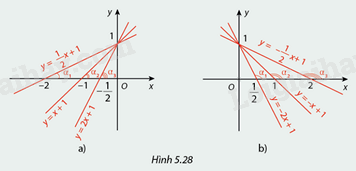
Phương pháp giải:
Quan sát Hình 5.28 và các hàm số ta có thể xác định được các hệ số \(a\), sau đó so sánh hệ số \(a\) của các hàm số đó và so sánh các góc \({\alpha _1},{\alpha _2},{\alpha _3}\).
Lời giải chi tiết:
a) Quan sát hình 5.28a ta thấy các góc \({\alpha _1} < {\alpha _2} < {\alpha _3}\)
Hàm số \(y = \frac{1}{2}x + 1\) có hệ số \({a_1} = \frac{1}{2}\)
Hàm số \(y = x + 1\) có hệ số \({a_2} = 1\)
Hàm số \(y = 2x + 1\) có hệ số \({a_3} = 2\)
Vậy qua đó ta được \(0 < {a_1} < {a_2} < {a_3}\)
b) Quan sát hình 5.28b ta thấy các góc \({\alpha _1} > {\alpha _2} > {\alpha _3}\)
Hàm số \(y = - 2x + 1\) có hệ số \({a_1} = - 2\)
Hàm số \(y = - x + 1\) có hệ số \({a_2} = - 1\)
Hàm số \(y = - \frac{1}{2}x + 1\) có hệ số \({a_3} = - \frac{1}{2}\)
Vậy qua đó ta được \({a_1} < {a_2} < {a_3} < 0\)
Cho hàm số bậc nhất \(y = ax\) có đồ thị là đường thẳng d như Hình 5.29. Tìm hệ số góc a.
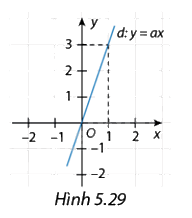
Phương pháp giải:
Hệ số \(a\) được gọi là hệ số góc của đường thẳng \(y = ax + b\) hay là hệ số góc của đồ thị hàm số \(y = ax + b\)\(\left( {a \ne 0} \right)\)
Lời giải chi tiết:
Quan sát hình 5.29, ta thấy hàm số bậc nhất \(y = ax\) có hệ số góc \(a = \frac{y}{x} = \frac{3}{1} = 3\).
Bạn Trọng tham gia cuộc thi trực tuyến “Tinh hoa Việt Nam” về những nét đặc sắc trong văn hóa nước ta. Khi mới tạo tài khoản dự thi, Trọng được tặng 50 điểm tích lũy. Mỗi khi trả lời đúng một câu hỏi, số điểm tích lũy T của Trọng được tăng theeo 5 điểm. Nếu trả lời sai câu hỏi thì không bị trừ điểm.
a) Tìm công thức biểu diễn hàm số T theo số câu hỏi n mà Trọng trả lời đúng
b) Tìm số điểm tích lũy của Trọng, biết rẳng Trọng đã trả lời đúng 18 câu hỏi.
Phương pháp giải:
Gọi số câu hỏi mà Trọng trả lời được là \(n\). Dựa vào các dữ liệu mà đề bài cho về mối quan hệ giữa các câu hỏi và điểm tích lũy, ta biểu diễn được hàm số T theo số câu hỏi \(n\) mà Trọng trả lời đúng, sau đó tìm số điểm tích lũy của Trọng khi trả lời được 18 câu hỏi.
Lời giải chi tiết:
a) Gọi số câu hỏi mà Trọng trả lời được là \(n\). Thì công thức biểu diễn hàm số T theo số câu hỏi \(n\) mà Trọng trả lời đúng là: \(T = 50 + 5n\)
b) Số điểm tích lũy của Trọng khi trả lời đúng 18 câu hỏi là: \(T = 50 + 5.8 = 90\) (điểm)
Trong Hình 5.30, các đường thẳng \(d\) và \(d'\) lần lượt chứa đồ thị quãng đường – thời gian của hai ô tô A và B chuyển động đều.
a) Tìm các số thích hợp cho ô trống trong Bảng 5.16.
b) Xác định hệ số góc của mỗi đường thẳng.
c) Tính tốc độ của mỗi xe. Em có nhận xét gì về tốc độ của mỗi xe và hệ số góc của đồ thị quãng đường – thời gian tương ứng?

Phương pháp giải:
Dựa vào cách xác định tọa độ trong mặt phẳng tọa độ học ở bài trước để tìm các số thích hợp cho Bảng 5.16.
Xác định hệ số góc của mỗi đường thẳng bằng cách thay các giá trị \(x,y\) vừa tìm được vào công thức \(y = ax + b\). Sau đó tính tốc độ của mỗi xe dựa vào công thức \(s = v.t\).
Lời giải chi tiết:
a) Quan sát Hình 5.30 ta được Bảng 5.16 như sau: 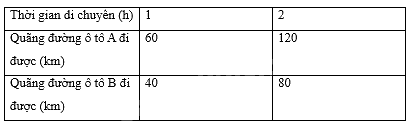
b) Quan sát Hình 5.30 ta thấy cả hai đường thẳng d và d’ đều đi qua gốc tọa độ \(O\left( {0;0} \right)\), vậy cả hai đường thẳng đều có dạng \(y = ax\).
Đường thẳng d đi qua điểm có tọa độ \(\left( {1;60} \right)\) thay vào hàm số \(y = ax\), ta có:
\(\begin{array}{l}60 = a.1\\ = > a = 60\end{array}\)
Vậy hệ số góc của đường thẳng d là \(a = 60\)
Đường thẳng d’ đi qua điểm có tọa độ \(\left( {1;40} \right)\) thay vào hàm số \(y = ax\), ta có:
\(\begin{array}{l}40 = a.1\\ = > a = 40\end{array}\)
Vậy hệ số góc của đường thẳng d’ là \(a = 40\)
c) Tốc độ của xe A là: \(v = \frac{s}{t} = \frac{{60}}{1} = 60\left( {km/h} \right)\)
Tốc độ của xe B là: \(v = \frac{s}{t} = \frac{{40}}{1} = 40\left( {km/h} \right)\)
Ta thấy tốc độ của mỗi xe bằng với hệ số góc của đồ thị quãng đường – thời gian tương ứng.
Mục 1 của chương trình Toán 8 thường tập trung vào việc ôn tập và hệ thống hóa các kiến thức cơ bản về số hữu tỉ, số thực, biểu thức đại số và các phép toán liên quan. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Mục 1 thường bao gồm các nội dung sau:
Trang 17 SGK Toán 8 thường chứa các bài tập ôn tập về số hữu tỉ. Các bài tập này yêu cầu học sinh thực hiện các phép toán cộng, trừ, nhân, chia số hữu tỉ, so sánh số hữu tỉ và tìm giá trị tuyệt đối của số hữu tỉ.
Ví dụ, bài tập 1 yêu cầu tính:
a) 1/2 + 1/3
b) 2/5 - 1/4
c) 3/7 * 2/9
d) 4/5 : 1/2
Để giải các bài tập này, học sinh cần nắm vững các quy tắc cộng, trừ, nhân, chia số hữu tỉ. Cụ thể:
Trang 18 SGK Toán 8 thường chứa các bài tập ôn tập về số thực. Các bài tập này yêu cầu học sinh thực hiện các phép toán cộng, trừ, nhân, chia số thực, so sánh số thực và tìm giá trị tuyệt đối của số thực.
Ví dụ, bài tập 2 yêu cầu tính:
a) 2.5 + 3.7
b) 4.8 - 1.2
c) 1.5 * 2.4
d) 6.3 : 0.9
Để giải các bài tập này, học sinh cần nắm vững các quy tắc cộng, trừ, nhân, chia số thực. Các quy tắc này tương tự như quy tắc cộng, trừ, nhân, chia số hữu tỉ.
Trang 19 SGK Toán 8 thường chứa các bài tập vận dụng về số hữu tỉ và số thực. Các bài tập này yêu cầu học sinh áp dụng kiến thức đã học để giải quyết các bài toán thực tế.
Ví dụ, bài tập 3 yêu cầu giải bài toán sau:
Một người nông dân có một mảnh đất hình chữ nhật có chiều dài 12m và chiều rộng 8m. Người nông dân muốn trồng rau trên mảnh đất đó. Hỏi người nông dân cần bao nhiêu mét vuông đất để trồng rau?
Để giải bài toán này, học sinh cần tính diện tích của mảnh đất hình chữ nhật. Diện tích của mảnh đất hình chữ nhật được tính bằng công thức:
Diện tích = chiều dài * chiều rộng
Trong trường hợp này, diện tích của mảnh đất là:
Diện tích = 12m * 8m = 96m2
Vậy người nông dân cần 96 mét vuông đất để trồng rau.
Để học tốt Toán 8, học sinh cần:
Chúc các em học tập tốt!