Chào mừng các em học sinh đến với bài giải chi tiết bài 6.42 trang 78 SGK Toán 8. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả nhất.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất trong môn Toán.
Vào một thời điểm trong ngày, \(B\) và \(D\) lần lượt là các bóng của điểm
Đề bài
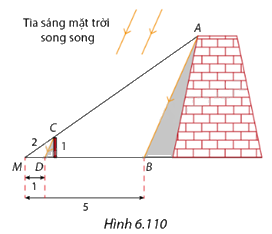
Vào một thời điểm trong ngày, \(B\) và \(D\) lần lượt là các bóng của điểm \(A\) trên mặt thành cổ và điểm \(C\) trên đỉnh cột lên mặt đất, các điểm \(M,C,A\) thẳng hàng và các điểm \(M,D,B\) thẳng hàng (Hình 6.110). Người ta đo được các khoảng cách \(MD = 1m,MB = 5m\) và \(MC = 2m.\)
a) Tính khoảng cách giữa hai điểm \(C\) và \(A.\)
b) Biết chiều cao của cây cột là \(1m,\) tính chiều cao của thành cổ.

Phương pháp giải - Xem chi tiết
Dựa vào định lí hai tam giác đồng dạng ở bài 4 để tìm khoảng cách 2 điểm C và A.
Áp dụng các trường hợp tam giác đồng dạng để tính chiều cao của thành cổ.
Lời giải chi tiết
a) Xét tam giác \(MDC\) và tam giác \(MBA\) , ta có:
\(CD//AB\) (do tia sáng mặt trời song song)
\(CD\) cắt \(MB,MA\) tại \(C,D\)
=> \(\Delta MDC\) ∽ \(\Delta MBA\)
Ta có tỉ số đồng dạng:
\(\frac{{MD}}{{MB}} = \frac{{MC}}{{MA}} \\ \frac{1}{5} = \frac{2}{{MA}} \Rightarrow MA = 10\)
=> \(CA = 10 - 2 = 8\)
Vậy khoảng cách giữa C và A là 8
b)
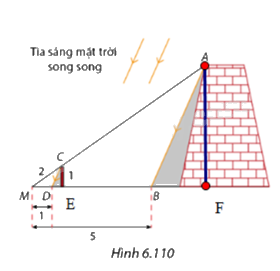
Kẻ \(AF\) vuông góc với \(MF\) .
Xét tam giác \(CME\) và tam giác \(AMF\) , ta có:
\(\widehat M\) là góc chung
\(\widehat {CEM} = \widehat {AFM} = 90^\circ \)
=> \(\Delta MCE\) ∽ \(\Delta MAF\) (g-g)
Ta có tỉ số đồng dạng:
\(\frac{{MC}}{{MA}} = \frac{{CE}}{{AF}} \\ \frac{2}{{10}} = \frac{1}{{AF}} \Rightarrow AF = 5\)
Bài 6.42 trang 78 SGK Toán 8 thuộc chương trình đại số lớp 8, tập trung vào việc vận dụng các kiến thức về hình chữ nhật để giải quyết các bài toán thực tế. Để giải bài này, học sinh cần nắm vững các tính chất của hình chữ nhật, đặc biệt là mối quan hệ giữa các cạnh đối song song và bằng nhau, các góc vuông, và đường chéo bằng nhau.
Đề bài yêu cầu chúng ta giải một bài toán liên quan đến hình chữ nhật, có thể là tính độ dài cạnh, diện tích, chu vi, hoặc chứng minh một tính chất nào đó. Việc đọc kỹ đề bài và xác định chính xác yêu cầu là bước đầu tiên quan trọng để giải quyết bài toán một cách hiệu quả.
Có nhiều phương pháp khác nhau để giải bài 6.42, tùy thuộc vào yêu cầu cụ thể của đề bài. Dưới đây là một số phương pháp thường được sử dụng:
Đề bài: Cho hình chữ nhật ABCD, AB = 8cm, BC = 6cm. Tính độ dài đường chéo AC.
Giải:
Vì ABCD là hình chữ nhật nên góc ABC vuông. Do đó, tam giác ABC là tam giác vuông tại B.
Áp dụng định lý Pitago vào tam giác ABC, ta có:
AC2 = AB2 + BC2
AC2 = 82 + 62 = 64 + 36 = 100
AC = √100 = 10cm
Vậy, độ dài đường chéo AC là 10cm.
Để củng cố kiến thức và kỹ năng giải bài tập về hình chữ nhật, các em có thể luyện tập thêm các bài toán tương tự trong SGK và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và tự tin hơn khi giải các bài toán khó.
Hình chữ nhật là một trong những hình học cơ bản và quan trọng trong chương trình Toán học. Ngoài các tính chất đã học, các em có thể tìm hiểu thêm về các loại hình chữ nhật đặc biệt như hình vuông, và các ứng dụng của hình chữ nhật trong thực tế.
Bài 6.42 trang 78 SGK Toán 8 là một bài tập quan trọng giúp các em hiểu sâu hơn về hình chữ nhật và các tính chất của nó. Hy vọng rằng, với bài giải chi tiết và phương pháp giải được trình bày trong bài viết này, các em sẽ tự tin hơn khi giải các bài tập tương tự.
| Công thức | Mô tả |
|---|---|
| Diện tích hình chữ nhật | S = a * b (a, b là chiều dài và chiều rộng) |
| Chu vi hình chữ nhật | P = 2 * (a + b) |
| Độ dài đường chéo | d = √(a2 + b2) |
Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!