Chào mừng bạn đến với bài học về Lý thuyết Chia đa thức cho đơn thức trong chương trình Toán 8. Đây là một phần kiến thức quan trọng, giúp bạn xây dựng nền tảng vững chắc cho các bài học tiếp theo.
Tại giaitoan.edu.vn, chúng tôi cung cấp tài liệu học tập đầy đủ, dễ hiểu, cùng với các bài tập thực hành đa dạng để bạn có thể nắm vững kiến thức một cách hiệu quả.
Chia đơn thức cho đơn thức như thế nào?
1. Chia đơn thức cho đơn thức
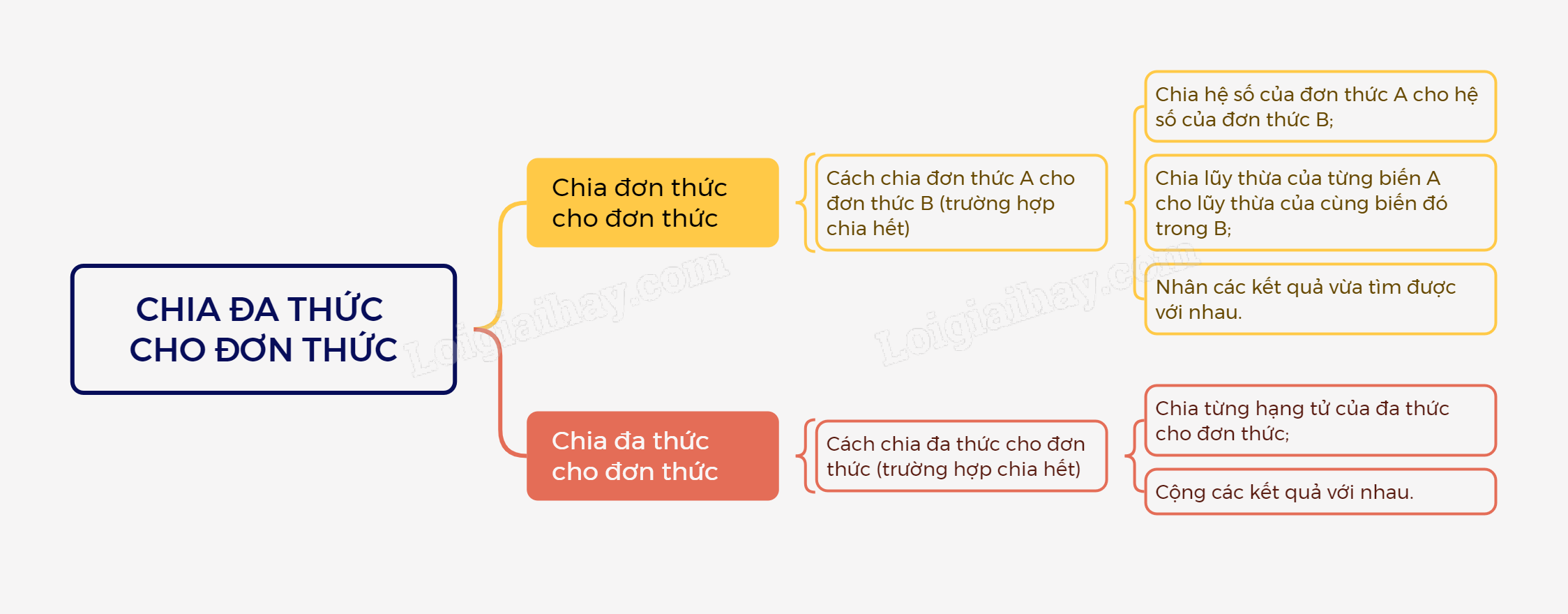
Muốn chia đơn thức A cho đơn thức B (với A chia hết cho B), ta làm như sau:
- Chia hệ số của A cho hệ số của B.
- Chia lũy thừa của từng biến trong A cho lũy thừa của cùng biến đó trong B.
- Nhân các kết quả vừa tìm được cho nhau.
Ví dụ:
\(\begin{array}{l}16{x^4}{y^3}:( - 8{x^3}{y^2})\\ = (16:( - 8)).({x^4}:{x^3}).\left( {{y^3}:{y^2}} \right)\\ = - 2xy\end{array}\)
+ Chia đa thức cho đơn thức như thế nào?
Muốn chia một đa thức cho một đơn thức (trường hợp chia hết), ta chia từng hạng tử của đa thức cho đơn thức đó, rồi cộng các kết quả tìm được với nhau.
Ví dụ:
\(\begin{array}{l}({x^2}y + {y^2}x):xy\\ = {x^2}y:xy + {y^2}x:xy\\ = x + y\end{array}\)
Trong chương trình Toán 8, phép chia đa thức cho đơn thức là một kỹ năng quan trọng mà học sinh cần nắm vững. Bài viết này sẽ trình bày chi tiết lý thuyết, ví dụ minh họa và các bài tập ứng dụng để giúp bạn hiểu rõ hơn về chủ đề này.
Phép chia đa thức cho đơn thức là phép toán ngược với phép nhân đa thức với đơn thức. Để thực hiện phép chia này, ta cần hiểu rõ các khái niệm cơ bản về đa thức, đơn thức và bậc của đa thức, đơn thức.
Để chia một đa thức cho một đơn thức, ta thực hiện các bước sau:
Công thức tổng quát:
(a + b + c) / d = a/d + b/d + c/d (với d ≠ 0)
Ví dụ 1: Chia đa thức 6x3y2 + 4x2y3 - 2xy cho đơn thức 2xy
Giải:
(6x3y2 + 4x2y3 - 2xy) / (2xy) = (6x3y2) / (2xy) + (4x2y3) / (2xy) - (2xy) / (2xy)
= 3x2y + 2xy2 - 1
Ví dụ 2: Chia đa thức 12x4 - 8x3 + 4x2 cho đơn thức 4x2
Giải:
(12x4 - 8x3 + 4x2) / (4x2) = (12x4) / (4x2) - (8x3) / (4x2) + (4x2) / (4x2)
= 3x2 - 2x + 1
Hãy thực hiện các phép chia đa thức sau cho đơn thức tương ứng:
Khi thực hiện phép chia đa thức cho đơn thức, cần chú ý đến các quy tắc về dấu và số mũ của các biến. Đảm bảo rằng bạn hiểu rõ các khái niệm cơ bản và áp dụng đúng công thức để đạt được kết quả chính xác.
Ngoài lý thuyết và ví dụ minh họa, bạn có thể tìm hiểu thêm về các ứng dụng của phép chia đa thức cho đơn thức trong việc giải các bài toán đại số và hình học. Việc luyện tập thường xuyên sẽ giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về Lý thuyết Chia đa thức cho đơn thức SGK Toán 8. Chúc bạn học tập tốt!