Định lí Thalès là một trong những kiến thức quan trọng bậc nhất trong chương trình Toán 8, là nền tảng để học tập các kiến thức về tam giác đồng dạng và các ứng dụng thực tế. Bài viết này sẽ cung cấp cho bạn một cách đầy đủ và dễ hiểu về lý thuyết Định lí Thalès, cùng với các ví dụ minh họa và bài tập vận dụng.
Tại giaitoan.edu.vn, chúng tôi luôn cố gắng mang đến những bài giảng chất lượng, giúp học sinh nắm vững kiến thức và tự tin hơn trong học tập.
Định lí Thalès là gì?
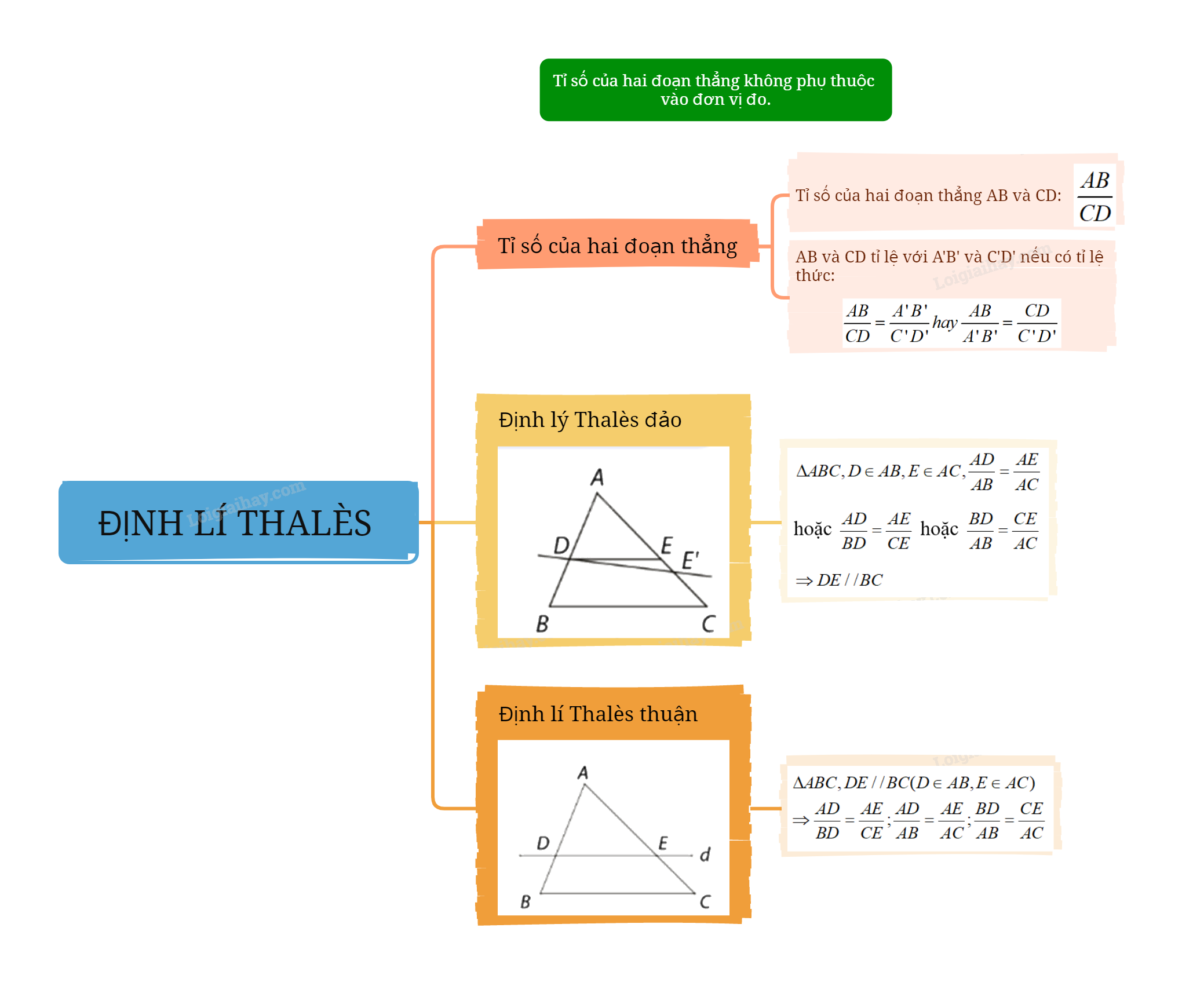
1. Tỉ số của hai đoạn thẳng
Tỉ số của hai đoạn thẳng AB và CD là tỉ số độ dài của chúng theo cùng một đơn vị đo, kí hiệu \(\frac{{AB}}{{CD}}\).
Hai đoạn thẳng AB và CD được gọi là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức \(\frac{{AB}}{{CD}} = \frac{{A'B'}}{{C'D'}}\,hay\,\frac{{AB}}{{A'B'}} = \frac{{CD}}{{C'D'}}\).
Tỉ số của hai đoạn thẳng không phụ thuộc vào đơn vị đo độ dài được sử dụng.
2. Định lí Thalès thuận
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương đương tỉ lệ.
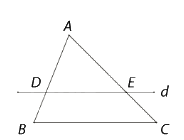
\(\begin{array}{l}\Delta ABC,DE//BC(D \in AB,E \in AC)\\ \Rightarrow \frac{{AD}}{{BD}} = \frac{{AE}}{{CE}};\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}};\frac{{BD}}{{AB}} = \frac{{CE}}{{AC}}\end{array}\)
3. Định lí Thalès đảo
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
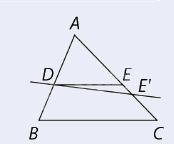
\(\Delta ABC,D \in AB,E \in AC,\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}\) hoặc \(\frac{{AD}}{{BD}} = \frac{{AE}}{{CE}}\) hoặc \(\frac{{BD}}{{AB}} = \frac{{CE}}{{AC}}\)
\( \Rightarrow DE//BC\)
Định lí Thalès là một trong những định lý cơ bản và quan trọng trong hình học lớp 8, liên quan đến việc xét tỉ lệ giữa các đoạn thẳng trên các cạnh của một tam giác khi có một đường thẳng song song với một cạnh của tam giác đó. Định lý này có ứng dụng rộng rãi trong việc giải các bài toán liên quan đến tam giác đồng dạng và các bài toán thực tế.
Định lí Thalès phát biểu như sau:
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó chia hai cạnh đó thành những đoạn thẳng tỉ lệ.
Cho tam giác ABC, đường thẳng d song song với BC cắt AB tại M và AC tại N. Khi đó:
Chứng minh Định lí Thalès dựa trên việc sử dụng các tam giác đồng dạng. Cụ thể, ta có thể chứng minh tam giác AMN đồng dạng với tam giác ABC bằng trường hợp góc - góc (g-g). Từ đó, suy ra tỉ lệ giữa các cạnh tương ứng, dẫn đến công thức Định lí Thalès.
Ví dụ 1: Cho tam giác ABC, M là trung điểm của AB, N là trung điểm của AC. Đường thẳng MN cắt BC tại D. Chứng minh BD = CD.
Giải: Vì M là trung điểm của AB và N là trung điểm của AC nên AM = MB và AN = NC. Do đó, MN là đường trung bình của tam giác ABC và MN song song với BC. Áp dụng Định lí Thalès, ta có:
AM/AB = AN/AC = 1/2
Suy ra, MN = 1/2 BC. Vì MN song song với BC nên tam giác AMN đồng dạng với tam giác ABC. Từ đó, suy ra BD = CD.
Bài 1: Cho tam giác ABC, D là một điểm trên cạnh AB, E là một điểm trên cạnh AC sao cho DE song song với BC. Biết AD = 4cm, DB = 6cm, AE = 5cm. Tính EC.
Bài 2: Cho tam giác ABC, MN song song với BC (M thuộc AB, N thuộc AC). Biết AM = 3cm, MB = 5cm, AN = 4cm. Tính NC.
Định lí Thalès có nhiều ứng dụng trong việc giải các bài toán hình học, đặc biệt là các bài toán liên quan đến tam giác đồng dạng. Một số ứng dụng cụ thể bao gồm:
Định lí Thalès còn có một dạng mở rộng, được gọi là hệ quả của Định lí Thalès. Hệ quả này phát biểu rằng:
Nếu một đường thẳng cắt hai cạnh của một tam giác và chia hai cạnh đó thành những đoạn thẳng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Lý thuyết Định lí Thalès là một kiến thức quan trọng trong chương trình Toán 8. Việc nắm vững lý thuyết này sẽ giúp bạn giải quyết các bài toán hình học một cách dễ dàng và hiệu quả hơn. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về Định lí Thalès.