Chào mừng các em học sinh lớp 8 đến với bài giải chi tiết mục 1 trang 14, 15 Sách Giáo Khoa Toán 8. Tại giaitoan.edu.vn, chúng tôi luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và giải quyết các bài tập một cách hiệu quả.
Bài giải này được trình bày rõ ràng, dễ hiểu, đi kèm với các phương pháp giải bài tập khác nhau, giúp các em hiểu sâu sắc hơn về nội dung bài học.
Tìm các số thích hợp cho các ô
Tìm các số thích hợp cho các ô ? trong đẳng thức sau:
\(\left( {4x{y^2}} \right).\left( {?.{x^?}{y^?}} \right) = 20{x^3}{y^5}\).
Giải thích cách làm của em.
Phương pháp giải:
Chia \(\left( {20{x^3}{y^5}} \right):\left( {4x{y^2}} \right)\), sau đó chia hệ số với hệ số, lũy thừa của từng biến cho nhau.
Lời giải chi tiết:
\(\begin{array}{l}\left( {4x{y^2}} \right).\left( {?.{x^?}{y^?}} \right) = 20{x^3}{y^5}\\ = \left( {4x{y^2}} \right).\left( {5{x^2}.{y^3}} \right) = 20{x^3}{y^5}\end{array}\)
Để tìm được số thích hợp, ta lấy \(\left( {20{x^3}{y^5}} \right):\left( {4x{y^2}} \right)\) hệ số chia cho hệ số, lũy thừa của từng biến cho nhau, ví dụ:
\(\left( {20{x^3}{y^5}} \right):\left( {4x{y^2}} \right) = \left( {?.{x^?}{y^?}} \right)\)
\(20:4 = 5\)
\({x^3}:x = {x^2}\)
\({y^5}:{y^2} = {y^3}\)
Vậy ta được kết quả là: \(5{x^2}.{y^3}\)
Tìm thương trong phép chia có đơn thức bị chia là \(18{x^4}{y^5}z\) và đơn thức chia là \(8{x^2}{y^3}\).
Phương pháp giải:
Để chia đơn thức A cho đơn thức B (trong trường hợp A chia hết cho B), ta làm như sau:
Lời giải chi tiết:
\(\begin{array}{l}\left( {18{x^4}{y^5}z} \right):\left( {8{x^2}{y^3}} \right) = \left( {18:8} \right).\left( {{x^4}:{x^2}} \right).\left( {{y^5}:{y^3}} \right).z\\ = \frac{9}{4}.{x^2}.{y^2}.z\end{array}\)
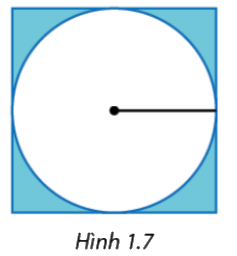
Trên một cánh đồng hình vuông, người ta đặt một hệ thống tưới tiêu tại điểm chính giữa của cánh đồng để tưới nước cho một khu vực hình tròn với đường kính bằng cạnh của cánh đồng (Hình 1.7). Tính tỉ số diện tích của khu vực được tưới nước và cánh đồng.
Phương pháp giải:
Gọi bán kính đường tròn là R. Áp dụng công thức tính diện tích hình vuông và tính diện tích hình tròn để tính được diện tích của khu vực được tưới nước và cánh đồng. Sau đó tính tỉ số diện tích.
Lời giải chi tiết:
Gọi bán kính đường tròn là R thì cạnh của cánh đồng hình vuông là 2R.
Diện tích cánh đồng hình vuông là: \({S_{hv}} = 2R.2R = 4{R^2}\)
Diện tích khu vực được tưới nước hình tròn là: \({S_{ht}} = 2\pi {R^2}\)
Vậy tỉ số diện tích của khu vực được tưới nước và cánh đồng là: \(\frac{{{S_{ht}}}}{{{S_{hv}}}} = \frac{{2\pi {R^2}}}{{4{R^2}}} = \frac{\pi }{2}\)
Tìm các số thích hợp cho các ô ? trong đẳng thức sau:
\(\left( {4x{y^2}} \right).\left( {?.{x^?}{y^?}} \right) = 20{x^3}{y^5}\).
Giải thích cách làm của em.
Phương pháp giải:
Chia \(\left( {20{x^3}{y^5}} \right):\left( {4x{y^2}} \right)\), sau đó chia hệ số với hệ số, lũy thừa của từng biến cho nhau.
Lời giải chi tiết:
\(\begin{array}{l}\left( {4x{y^2}} \right).\left( {?.{x^?}{y^?}} \right) = 20{x^3}{y^5}\\ = \left( {4x{y^2}} \right).\left( {5{x^2}.{y^3}} \right) = 20{x^3}{y^5}\end{array}\)
Để tìm được số thích hợp, ta lấy \(\left( {20{x^3}{y^5}} \right):\left( {4x{y^2}} \right)\) hệ số chia cho hệ số, lũy thừa của từng biến cho nhau, ví dụ:
\(\left( {20{x^3}{y^5}} \right):\left( {4x{y^2}} \right) = \left( {?.{x^?}{y^?}} \right)\)
\(20:4 = 5\)
\({x^3}:x = {x^2}\)
\({y^5}:{y^2} = {y^3}\)
Vậy ta được kết quả là: \(5{x^2}.{y^3}\)
Tìm thương trong phép chia có đơn thức bị chia là \(18{x^4}{y^5}z\) và đơn thức chia là \(8{x^2}{y^3}\).
Phương pháp giải:
Để chia đơn thức A cho đơn thức B (trong trường hợp A chia hết cho B), ta làm như sau:
Lời giải chi tiết:
\(\begin{array}{l}\left( {18{x^4}{y^5}z} \right):\left( {8{x^2}{y^3}} \right) = \left( {18:8} \right).\left( {{x^4}:{x^2}} \right).\left( {{y^5}:{y^3}} \right).z\\ = \frac{9}{4}.{x^2}.{y^2}.z\end{array}\)
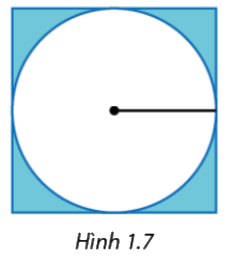
Trên một cánh đồng hình vuông, người ta đặt một hệ thống tưới tiêu tại điểm chính giữa của cánh đồng để tưới nước cho một khu vực hình tròn với đường kính bằng cạnh của cánh đồng (Hình 1.7). Tính tỉ số diện tích của khu vực được tưới nước và cánh đồng.
Phương pháp giải:
Gọi bán kính đường tròn là R. Áp dụng công thức tính diện tích hình vuông và tính diện tích hình tròn để tính được diện tích của khu vực được tưới nước và cánh đồng. Sau đó tính tỉ số diện tích.
Lời giải chi tiết:
Gọi bán kính đường tròn là R thì cạnh của cánh đồng hình vuông là 2R.
Diện tích cánh đồng hình vuông là: \({S_{hv}} = 2R.2R = 4{R^2}\)
Diện tích khu vực được tưới nước hình tròn là: \({S_{ht}} = 2\pi {R^2}\)
Vậy tỉ số diện tích của khu vực được tưới nước và cánh đồng là: \(\frac{{{S_{ht}}}}{{{S_{hv}}}} = \frac{{2\pi {R^2}}}{{4{R^2}}} = \frac{\pi }{2}\)
Mục 1 trang 14, 15 SGK Toán 8 thường xoay quanh các kiến thức cơ bản về hình học, đại số, hoặc các bài toán thực tế ứng dụng. Để giải quyết các bài tập trong mục này, học sinh cần nắm vững các định nghĩa, tính chất, và công thức liên quan.
Thông thường, mục này sẽ giới thiệu một khái niệm mới hoặc mở rộng kiến thức đã học. Ví dụ, có thể là về các loại góc, các tính chất của đường thẳng song song, hoặc các phép biến đổi đơn giản trên đa thức. Việc hiểu rõ nội dung lý thuyết là bước đầu tiên quan trọng để giải quyết các bài tập.
Bài 1: Cho hai đường thẳng a và b song song. Một đường thẳng c cắt a tại A và b tại B. Tính số đo góc ABx nếu góc BAx bằng 60 độ.
Giải:
Để giải bài tập một cách hiệu quả, học sinh cần:
Giaitoan.edu.vn là một website học toán online uy tín, cung cấp:
Hãy truy cập giaitoan.edu.vn ngay hôm nay để khám phá thế giới toán học đầy thú vị và đạt kết quả cao trong học tập!
| Công thức | Mô tả |
|---|---|
| Hai góc đối đỉnh | Bằng nhau |
| Hai góc kề bù | Tổng bằng 180 độ |
| Hai đường thẳng song song | Không có điểm chung |