Chào mừng các em học sinh đến với bài giải chi tiết mục 3 trang 20, 21 sách giáo khoa Toán 8. Tại giaitoan.edu.vn, chúng tôi cung cấp các lời giải bài tập Toán 8 được trình bày rõ ràng, dễ hiểu, giúp các em tự tin hơn trong quá trình học tập.
Mục tiêu của chúng tôi là hỗ trợ các em học sinh nắm vững kiến thức Toán học, rèn luyện kỹ năng giải bài tập và đạt kết quả tốt nhất trong các kỳ thi.
Cho hai đường thẳng
Cho hai hàm số bậc nhất \(y = mx - 3\) và \(y = 5x + n\). Tìm giá trị của m và n để đồ thị của hai hàm số đã cho là:
a) Hai đường thẳng song song
b) Hai đường thẳng cắt nhau.
Phương pháp giải:
Dựa vào điều kiện của hai đường thẳng song song và hai đường thẳng cắt nhau để tìm giá trị của m và n.
Lời giải chi tiết:
a) Để hai hàm số bậc nhất \(y = mx - 3\) và \(y = 5x + n\) là hai đường thẳng song song thì \(a = a',b \ne b'\) => \(m = 5,n \ne - 3\)
b) Để hai hàm số bậc nhất \(y = mx - 3\) và \(y = 5x + n\) là hai đường thẳng cắt nhau thì \(a \ne a'\) => \(m \ne 5\).
Cho hai đường thẳng \(y = 2x - 1\) và \(y = x + 1\).
a) Hai đường thẳng này có song song với nhau không? Từ đó kết luận về số giao điểm của chúng
b) Vẽ hai đường thẳng đó trên cùng một hệ trục tọa độ và tìm tọa độ giao điểm (nếu có).
Phương pháp giải:
Điều kiện của hai đường thẳng cắt nhau là \(a = a',b \ne b'\) và ngược lại. Sau đó vẽ hai đường thẳng đó trên cùng một hệ trục tọa độ và tìm tọa độ giao điểm.
Lời giải chi tiết:
a) Hai đường thẳng này không song song với nhau vì hệ số góc không bằng nhau. Vì vậy hai đường thẳng này sẽ cắt nhau và chỉ có một giao điểm
b) Vẽ hệ trục tọa độ \(Oxy\).
Hàm số \(y = 2x - 1\)
Cho \(x = 0 = > y = - 1\)
Cho \(y = 0 = > x = \frac{1}{2}\)
Vậy đồ thị hàm số \(y = 2x - 1\) là đường thẳng đi qua hai điểm \(A\left( {0; - 1} \right),B\left( {\frac{1}{2};0} \right)\)
Hàm số \(y = x + 1\)
Cho \(x = 0 = > y = 1\)
Cho \(y = 0 = > x = - 1\)
Vậy đồ thị hàm số \(y = x + 1\) là đường thẳng đi qua hai điểm \(C\left( {0;1} \right),D\left( { - 1;0} \right)\)
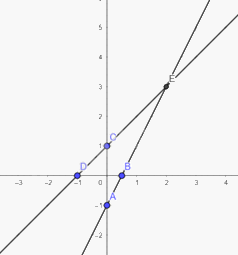
Giao điểm \(E\left( {2;3} \right)\).
Một bè gỗ trôi theo dòng nước trên một khúc sông từ bến A đến bến B với tốc độ 4 km/h. Xuất phát cùng lúc với bè gỗ, một thuyền ngược dòng từ B về A với tốc độ 8 km/h. Hai bến sông A, B cách nhau 12 km.
a) Viết hàm số biểu thị quãng đường bè gỗ đi được sau x giờ
b) Viết hàm số biểu thị quãng đường thuyền còn phải đi để đến A sau x giờ.
c) Vẽ đồ thị của hai hàm số trên cùng một hệ trục tọa độ. Từ đồ thị hãy cho biết sau bao lâu kể từ khi cùng xuất phát thì bè gỗ và thuyền gặp nhau.
Phương pháp giải:
Dựa vào mối quan hệ giữa quãng đường và tốc độ đề bài đưa ra viết hàm số biểu thị quãng đường bè gỗ đi được sau x giờ và hàm số biểu thị quãng đường thuyền còn phải đi để đến A sau x giờ. Sau đó vẽ đồ thị của hai hàm số, áp dụng điều kiện đồ thị hai đường thẳng cắt nhau xác định giao điểm.
Lời giải chi tiết:
a) Hàm số biểu thị quãng đường bè gỗ đi được sau x giờ là: \(y = 4x\)
b) Hàm số biểu thị quãng đường thuyền còn phải đi để đến A sau x giờ là: \(y = 12 - 8x\)
c) Vẽ hệ trục tọa độ \(Oxy\)
Hàm số \(y = 4x\) đi qua gốc tọa độ \(O\left( {0;0} \right)\)
Cho \(x - 1 = > y = 4\)
Vậy hàm số \(y = 4x\) là đường thẳng đi qua hai điểm \(O\left( {0;0} \right),A\left( {1;4} \right)\)
Hàm số \(y = 12 - 8x\)
Cho \(x = 0 = > y = 12\)
Cho \(y = 0 = > x = \frac{3}{2}\)
Vậy hàm số \(y = 12 - 8x\) là đường thẳng đi qua hai điểm \(B\left( {0;12} \right),C\left( {\frac{3}{2};0} \right)\)
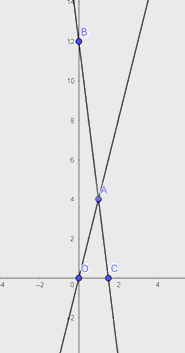
Từ đồ thị của hai hàm số trên ta thấy hai đường thẳng giao nhau tại \(A\left( {1;4} \right)\) có nghĩa là sau 1 giờ kể từ khi cùng xuất phát thì bè gỗ và thuyền gặp nhau.
Cho hai đường thẳng \(y = 2x - 1\) và \(y = x + 1\).
a) Hai đường thẳng này có song song với nhau không? Từ đó kết luận về số giao điểm của chúng
b) Vẽ hai đường thẳng đó trên cùng một hệ trục tọa độ và tìm tọa độ giao điểm (nếu có).
Phương pháp giải:
Điều kiện của hai đường thẳng cắt nhau là \(a = a',b \ne b'\) và ngược lại. Sau đó vẽ hai đường thẳng đó trên cùng một hệ trục tọa độ và tìm tọa độ giao điểm.
Lời giải chi tiết:
a) Hai đường thẳng này không song song với nhau vì hệ số góc không bằng nhau. Vì vậy hai đường thẳng này sẽ cắt nhau và chỉ có một giao điểm
b) Vẽ hệ trục tọa độ \(Oxy\).
Hàm số \(y = 2x - 1\)
Cho \(x = 0 = > y = - 1\)
Cho \(y = 0 = > x = \frac{1}{2}\)
Vậy đồ thị hàm số \(y = 2x - 1\) là đường thẳng đi qua hai điểm \(A\left( {0; - 1} \right),B\left( {\frac{1}{2};0} \right)\)
Hàm số \(y = x + 1\)
Cho \(x = 0 = > y = 1\)
Cho \(y = 0 = > x = - 1\)
Vậy đồ thị hàm số \(y = x + 1\) là đường thẳng đi qua hai điểm \(C\left( {0;1} \right),D\left( { - 1;0} \right)\)
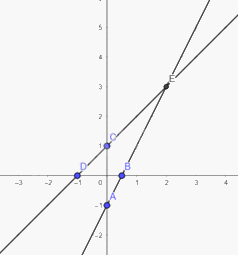
Giao điểm \(E\left( {2;3} \right)\).
Cho hai hàm số bậc nhất \(y = mx - 3\) và \(y = 5x + n\). Tìm giá trị của m và n để đồ thị của hai hàm số đã cho là:
a) Hai đường thẳng song song
b) Hai đường thẳng cắt nhau.
Phương pháp giải:
Dựa vào điều kiện của hai đường thẳng song song và hai đường thẳng cắt nhau để tìm giá trị của m và n.
Lời giải chi tiết:
a) Để hai hàm số bậc nhất \(y = mx - 3\) và \(y = 5x + n\) là hai đường thẳng song song thì \(a = a',b \ne b'\) => \(m = 5,n \ne - 3\)
b) Để hai hàm số bậc nhất \(y = mx - 3\) và \(y = 5x + n\) là hai đường thẳng cắt nhau thì \(a \ne a'\) => \(m \ne 5\).
Một bè gỗ trôi theo dòng nước trên một khúc sông từ bến A đến bến B với tốc độ 4 km/h. Xuất phát cùng lúc với bè gỗ, một thuyền ngược dòng từ B về A với tốc độ 8 km/h. Hai bến sông A, B cách nhau 12 km.
a) Viết hàm số biểu thị quãng đường bè gỗ đi được sau x giờ
b) Viết hàm số biểu thị quãng đường thuyền còn phải đi để đến A sau x giờ.
c) Vẽ đồ thị của hai hàm số trên cùng một hệ trục tọa độ. Từ đồ thị hãy cho biết sau bao lâu kể từ khi cùng xuất phát thì bè gỗ và thuyền gặp nhau.
Phương pháp giải:
Dựa vào mối quan hệ giữa quãng đường và tốc độ đề bài đưa ra viết hàm số biểu thị quãng đường bè gỗ đi được sau x giờ và hàm số biểu thị quãng đường thuyền còn phải đi để đến A sau x giờ. Sau đó vẽ đồ thị của hai hàm số, áp dụng điều kiện đồ thị hai đường thẳng cắt nhau xác định giao điểm.
Lời giải chi tiết:
a) Hàm số biểu thị quãng đường bè gỗ đi được sau x giờ là: \(y = 4x\)
b) Hàm số biểu thị quãng đường thuyền còn phải đi để đến A sau x giờ là: \(y = 12 - 8x\)
c) Vẽ hệ trục tọa độ \(Oxy\)
Hàm số \(y = 4x\) đi qua gốc tọa độ \(O\left( {0;0} \right)\)
Cho \(x - 1 = > y = 4\)
Vậy hàm số \(y = 4x\) là đường thẳng đi qua hai điểm \(O\left( {0;0} \right),A\left( {1;4} \right)\)
Hàm số \(y = 12 - 8x\)
Cho \(x = 0 = > y = 12\)
Cho \(y = 0 = > x = \frac{3}{2}\)
Vậy hàm số \(y = 12 - 8x\) là đường thẳng đi qua hai điểm \(B\left( {0;12} \right),C\left( {\frac{3}{2};0} \right)\)
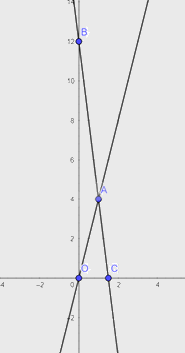
Từ đồ thị của hai hàm số trên ta thấy hai đường thẳng giao nhau tại \(A\left( {1;4} \right)\) có nghĩa là sau 1 giờ kể từ khi cùng xuất phát thì bè gỗ và thuyền gặp nhau.
Mục 3 trong sách giáo khoa Toán 8 trang 20 và 21 thường tập trung vào các dạng bài tập về đa thức, các phép toán trên đa thức, và các ứng dụng của đa thức trong giải toán. Việc nắm vững kiến thức về đa thức là nền tảng quan trọng để học tốt các chương trình Toán học ở các lớp trên.
Mục 3 thường bao gồm các nội dung sau:
Dưới đây là hướng dẫn giải một số dạng bài tập thường gặp trong Mục 3 trang 20, 21 SGK Toán 8:
Để xác định bậc của đa thức, ta cần tìm số mũ lớn nhất của biến trong đa thức. Ví dụ, đa thức 3x2 + 2x - 1 có bậc là 2.
Khi thực hiện các phép toán trên đa thức, ta cần tuân thủ các quy tắc sau:
Khi giải các bài toán ứng dụng, ta cần:
Bài tập: Tìm bậc của đa thức P(x) = 5x3 - 2x2 + x - 7.
Giải: Đa thức P(x) có các số hạng là 5x3, -2x2, x, và -7. Số mũ lớn nhất của biến x là 3. Vậy, bậc của đa thức P(x) là 3.
Để giải bài tập Mục 3 trang 20, 21 SGK Toán 8 một cách hiệu quả, các em cần:
Ngoài sách giáo khoa, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn trong việc giải các bài tập Mục 3 trang 20, 21 SGK Toán 8. Chúc các em học tập tốt và đạt kết quả cao!