Chào mừng các em học sinh lớp 8 đến với chuyên mục giải bài tập Toán 8 của giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 8, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Ở bài viết này, chúng ta sẽ cùng nhau giải quyết các bài tập trong mục 1 trang 54, 55, 56, 57 SGK Toán 8. Các lời giải được trình bày một cách rõ ràng, logic, kèm theo các ví dụ minh họa để các em dễ dàng theo dõi và áp dụng.
Hoàn thành bảng dưới đây bằng cách với mỗi trường hợp,
Tìm độ dài thích hợp cho ô \(?\).
a) \(\Delta {\rm{DEF}}\) vuông tại \(E\) có \({?^2} + {?^2} = {?^2}\)( định lí Pythagore)
b) \(\Delta MNP\) vuông tại \(P\)có \({?^2} + {?^2} = {?^2}\) ( định lí Pythagore)
c) \(\Delta ABC\) vuông tại \(?\) có \(A{B^2} = A{C^2} + {?^2}\)( định lí Pythagore)
Phương pháp giải:
Sử dụng định lí Pythagore với các tam giác tương ứng.
Lời giải chi tiết:
a) \(\Delta {\rm{DEF}}\) vuông tại \(E\) có \(D{E^2}{\rm{ + E}}{{\rm{F}}^2} = D{F^2}\)( định lí Pythagore)
b) \(\Delta MNP\) vuông tại \(P\)có \(M{P^2} + N{P^2} = M{N^2}\)( định lí Pythagore)
c) \(\Delta ABC\) vuông tại \(C\) có \(A{B^2} = A{C^2} + B{C^2}\)( định lí Pythagore)
Các nhà sản xuất thường dựa vào độ dài đường chéo của màn hình điện thoại (tính theo đơn vị inch) để xác định kích thước màn hình chiếc điện thoại đó. Màn hình một chiếc điện thoại có chiều rộng \(6,9\,cm,\) chiều dài \(15\,cm\) thì có kích thước màn hình là bao nhiêu inch (làm tròn kết quả đến hàng phần mười)? Biết 1 inch\( \approx 3,54\,cm.\)
Phương pháp giải:
Sử dụng định lí Pythagore: trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Lời giải chi tiết:
Độ dài đường chéo của màn hình điện thoại là:
\(\sqrt {{{\left( {6,9} \right)}^2} + {{15}^2}} = 16,5\left( {cm} \right)\)
Kích thước màn hình dài: \(16,5:3,54 = 4,7\left( {inch} \right)\)
Tìm độ dài \(x\) trong các tam giác vuông ở hình 3.5
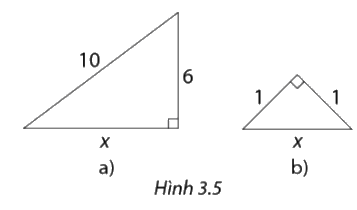
Phương pháp giải:
Sử dụng định lí Pythagore: trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Lời giải chi tiết:
a) Ta có:
\(\begin{array}{l}{x^2} + {6^2} = {10^2}\\ \Rightarrow {x^2} = 100 - 36 = 64\\ \Rightarrow x = 8\end{array}\)
b) Ta có
\(\begin{array}{l}{1^2} + {1^2} = {x^2}\\ \Rightarrow x = \sqrt 2 \end{array}\)
Hình 3.8 mô phỏng thiết kế của đoạn lên dốc dành cho người ngồi xe lăn trong một công trình xây dựng. Theo quy chuẩn quốc gia về xây dựng công trình đảm bảo người khuyết tật tiếp cận sử dụng (QCVN 10:2014/BXD), độ dốc không được lớn hơn \(\frac{1}{{12}}\), nghĩa là \(\frac{h}{d} \le \frac{1}{{12}}\). Thiết kế này có đáp ứng đúng quy chuẩn trên không?

Phương pháp giải:
Sử dụng định lí Pythagore: trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Lời giải chi tiết:
Ta có \(d = \sqrt {{{500}^2} - {h^2}} = \sqrt {{{500}^2} - {{40}^2}} = 60\sqrt {69} \left( {mm} \right)\)
Ta tính \(\frac{h}{d} = \frac{{40}}{{60\sqrt {69} }} \approx 0,08 < \frac{1}{{12}}\)
Vậy thiết kế trong hình vẽ đã đáp ứng đúng quy chuẩn.
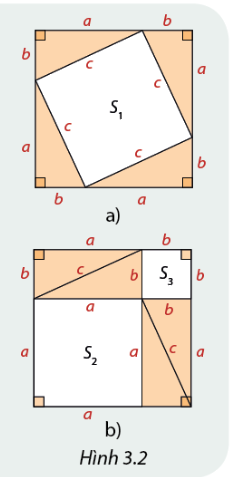
Dùng giấy màu, cắt tám tam giác vuông bằng nhau. Với mỗi tam giác vuông này, gọi độ dài các cạn
h góc vuông là \(a,b\) và độ dài cạnh huyền là \(c\). Dùng giấy bìa trắng, cắt hai hình vuông có cạnh bằng \(a + b\).
1. Đặt bốn tam giác vuông lên tấm bìa hình vuông thứ nhất như hình 3.2. Tính diện tích \({S_1}\) của phần bìa màu trắng không bị che lấp.
2. Đặt bốn tam giác vuông còn lại lên tấm bìa hình vuông thứ hai như hình 3.2b. Tính diện tích \({S_2},{S_3}\) của phần bìa màu trắng không bị che lấp.
3. So sánh \({S_1}\) và \({S_2} + {S_3}\), từ đó nhận xét mối quan hệ giữa \({c^2}\) và \({a^2} + {b^2}.\)
Phương pháp giải:
1. Diện tích phần bìa màu trắng là diện tích hình vuông có cạnh bằng \(c.\)
2. Diện tích của phần bìa màu trắng không bị che lấp là tổng diện tích hai hình vuông có cạnh lần lượt là \(a\) và \(b.\)
3. So sánh \({S_1}\) và \({S_2} + {S_3}\), từ đó nhận xét mối quan hệ giữa \({c^2}\) và \({a^2} + {b^2}.\)
Lời giải chi tiết:
1. Diện tích \({S_1}\) của phần bìa màu trắng không bị che lấp là \({c^2}.\)
2. Diện tích \({S_2},{S_3}\) của phần bìa màu trắng không bị che lấp là: \({a^2} + {b^2}\)
3. Ta thấy diện tích \({S_1}\) và \({S_2},{S_3}\) đều bằng diện tích tấm bìa hình vuông lớn trừ đi diện tích 4 tam giác bằng nhau. Nên \({S_1} = {S_2} + {S_3}\) hay suy ra \({a^2} + {b^2} = {c^2}\)
Hoàn thành bảng dưới đây bằng cách với mỗi trường hợp, vẽ một tam giác vuông có các cạnh góc vuông bằng \(a\left( {cm} \right)\),\(b\left( {cm} \right)\) và đo độ dài cạnh huyền \(c\left( {cm} \right)\) tương ứng.
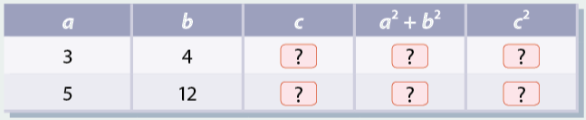
Có nhận xét gì về quan hệ giữa \({c^2}\) và \({a^2} + {b^2}\) trong mỗi trường hợp?
Phương pháp giải:
Hoàn thành bảng vẽ theo yêu cầu bài toán.
Sau đó nhận xét.
Lời giải chi tiết:
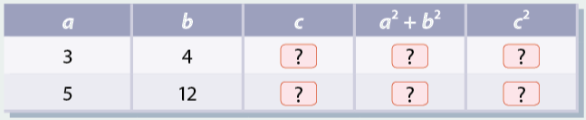
Ta có bảng sau:
\(a\) | \(b\) | \(c\) | \({a^2} + {b^2}\) | \({c^2}\) |
\(3\) | \(4\) | \(5\) | \(25\) | \(25\) |
\(5\) | \(12\) | \(13\) | \(169\) | \(169\) |
Ta thấy trong các trường hợp này \({a^2} + {b^2} = {c^2}\)
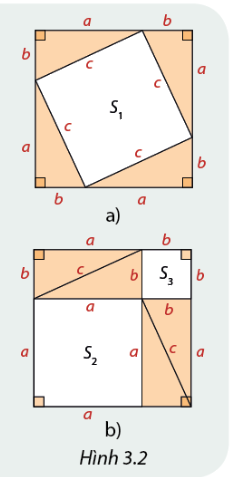
Dùng giấy màu, cắt tám tam giác vuông bằng nhau. Với mỗi tam giác vuông này, gọi độ dài các cạn
h góc vuông là \(a,b\) và độ dài cạnh huyền là \(c\). Dùng giấy bìa trắng, cắt hai hình vuông có cạnh bằng \(a + b\).
1. Đặt bốn tam giác vuông lên tấm bìa hình vuông thứ nhất như hình 3.2. Tính diện tích \({S_1}\) của phần bìa màu trắng không bị che lấp.
2. Đặt bốn tam giác vuông còn lại lên tấm bìa hình vuông thứ hai như hình 3.2b. Tính diện tích \({S_2},{S_3}\) của phần bìa màu trắng không bị che lấp.
3. So sánh \({S_1}\) và \({S_2} + {S_3}\), từ đó nhận xét mối quan hệ giữa \({c^2}\) và \({a^2} + {b^2}.\)
Phương pháp giải:
1. Diện tích phần bìa màu trắng là diện tích hình vuông có cạnh bằng \(c.\)
2. Diện tích của phần bìa màu trắng không bị che lấp là tổng diện tích hai hình vuông có cạnh lần lượt là \(a\) và \(b.\)
3. So sánh \({S_1}\) và \({S_2} + {S_3}\), từ đó nhận xét mối quan hệ giữa \({c^2}\) và \({a^2} + {b^2}.\)
Lời giải chi tiết:
1. Diện tích \({S_1}\) của phần bìa màu trắng không bị che lấp là \({c^2}.\)
2. Diện tích \({S_2},{S_3}\) của phần bìa màu trắng không bị che lấp là: \({a^2} + {b^2}\)
3. Ta thấy diện tích \({S_1}\) và \({S_2},{S_3}\) đều bằng diện tích tấm bìa hình vuông lớn trừ đi diện tích 4 tam giác bằng nhau. Nên \({S_1} = {S_2} + {S_3}\) hay suy ra \({a^2} + {b^2} = {c^2}\)
Tìm độ dài thích hợp cho ô \(?\).
a) \(\Delta {\rm{DEF}}\) vuông tại \(E\) có \({?^2} + {?^2} = {?^2}\)( định lí Pythagore)
b) \(\Delta MNP\) vuông tại \(P\)có \({?^2} + {?^2} = {?^2}\) ( định lí Pythagore)
c) \(\Delta ABC\) vuông tại \(?\) có \(A{B^2} = A{C^2} + {?^2}\)( định lí Pythagore)
Phương pháp giải:
Sử dụng định lí Pythagore với các tam giác tương ứng.
Lời giải chi tiết:
a) \(\Delta {\rm{DEF}}\) vuông tại \(E\) có \(D{E^2}{\rm{ + E}}{{\rm{F}}^2} = D{F^2}\)( định lí Pythagore)
b) \(\Delta MNP\) vuông tại \(P\)có \(M{P^2} + N{P^2} = M{N^2}\)( định lí Pythagore)
c) \(\Delta ABC\) vuông tại \(C\) có \(A{B^2} = A{C^2} + B{C^2}\)( định lí Pythagore)
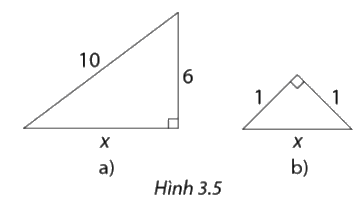
Tìm độ dài \(x\) trong các tam giác vuông ở hình 3.5
Phương pháp giải:
Sử dụng định lí Pythagore: trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Lời giải chi tiết:
a) Ta có:
\(\begin{array}{l}{x^2} + {6^2} = {10^2}\\ \Rightarrow {x^2} = 100 - 36 = 64\\ \Rightarrow x = 8\end{array}\)
b) Ta có
\(\begin{array}{l}{1^2} + {1^2} = {x^2}\\ \Rightarrow x = \sqrt 2 \end{array}\)
Các nhà sản xuất thường dựa vào độ dài đường chéo của màn hình điện thoại (tính theo đơn vị inch) để xác định kích thước màn hình chiếc điện thoại đó. Màn hình một chiếc điện thoại có chiều rộng \(6,9\,cm,\) chiều dài \(15\,cm\) thì có kích thước màn hình là bao nhiêu inch (làm tròn kết quả đến hàng phần mười)? Biết 1 inch\( \approx 3,54\,cm.\)
Phương pháp giải:
Sử dụng định lí Pythagore: trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Lời giải chi tiết:
Độ dài đường chéo của màn hình điện thoại là:
\(\sqrt {{{\left( {6,9} \right)}^2} + {{15}^2}} = 16,5\left( {cm} \right)\)
Kích thước màn hình dài: \(16,5:3,54 = 4,7\left( {inch} \right)\)
Hình 3.8 mô phỏng thiết kế của đoạn lên dốc dành cho người ngồi xe lăn trong một công trình xây dựng. Theo quy chuẩn quốc gia về xây dựng công trình đảm bảo người khuyết tật tiếp cận sử dụng (QCVN 10:2014/BXD), độ dốc không được lớn hơn \(\frac{1}{{12}}\), nghĩa là \(\frac{h}{d} \le \frac{1}{{12}}\). Thiết kế này có đáp ứng đúng quy chuẩn trên không?

Phương pháp giải:
Sử dụng định lí Pythagore: trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Lời giải chi tiết:
Ta có \(d = \sqrt {{{500}^2} - {h^2}} = \sqrt {{{500}^2} - {{40}^2}} = 60\sqrt {69} \left( {mm} \right)\)
Ta tính \(\frac{h}{d} = \frac{{40}}{{60\sqrt {69} }} \approx 0,08 < \frac{1}{{12}}\)
Vậy thiết kế trong hình vẽ đã đáp ứng đúng quy chuẩn.
Hoàn thành bảng dưới đây bằng cách với mỗi trường hợp, vẽ một tam giác vuông có các cạnh góc vuông bằng \(a\left( {cm} \right)\),\(b\left( {cm} \right)\) và đo độ dài cạnh huyền \(c\left( {cm} \right)\) tương ứng.
Có nhận xét gì về quan hệ giữa \({c^2}\) và \({a^2} + {b^2}\) trong mỗi trường hợp?
Phương pháp giải:
Hoàn thành bảng vẽ theo yêu cầu bài toán.
Sau đó nhận xét.
Lời giải chi tiết:
Ta có bảng sau:
\(a\) | \(b\) | \(c\) | \({a^2} + {b^2}\) | \({c^2}\) |
\(3\) | \(4\) | \(5\) | \(25\) | \(25\) |
\(5\) | \(12\) | \(13\) | \(169\) | \(169\) |
Ta thấy trong các trường hợp này \({a^2} + {b^2} = {c^2}\)
Mục 1 của chương trình Toán 8 thường tập trung vào việc ôn tập và hệ thống hóa các kiến thức về đa thức, phân thức đại số. Việc nắm vững các kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Mục 1 thường bao gồm các nội dung sau:
Bài 1: (Đề bài)...
Lời giải:...
Bài 2: (Đề bài)...
Lời giải:...
Bài 3: (Đề bài)...
Lời giải:...
Bài 4: (Đề bài)...
Lời giải:...
Bài 5: (Đề bài)...
Lời giải:...
Bài 6: (Đề bài)...
Lời giải:...
Bài 7: (Đề bài)...
Lời giải:...
Bài 8: (Đề bài)...
Lời giải:...
Khi giải các bài tập về đa thức và phân thức đại số, các em cần chú ý:
Ví dụ: Cho biểu thức A = (x + 2)(x - 2) + 4. Hãy rút gọn biểu thức A.
Lời giải:
A = (x + 2)(x - 2) + 4 = x2 - 4 + 4 = x2
Vậy, biểu thức A được rút gọn là x2.
Việc giải bài tập SGK Toán 8 không chỉ giúp các em nắm vững kiến thức mà còn rèn luyện kỹ năng giải toán, tư duy logic và khả năng tự học. Các bài tập trong SGK được thiết kế theo mức độ khó tăng dần, giúp các em làm quen với các dạng bài khác nhau và phát triển khả năng giải quyết vấn đề.
Ngoài ra, việc giải bài tập SGK còn giúp các em chuẩn bị tốt cho các kỳ thi học kỳ và thi tuyển vào các trường THPT chuyên.
Giaitoan.edu.vn là một website học toán online uy tín, cung cấp đầy đủ các tài liệu học tập, bài giảng, bài tập và lời giải chi tiết cho các môn Toán từ lớp 6 đến lớp 12. Chúng tôi luôn cập nhật những kiến thức mới nhất và phương pháp giải toán hiệu quả nhất để giúp các em học tập tốt hơn.
Hãy truy cập giaitoan.edu.vn để khám phá thêm nhiều tài liệu hữu ích và cùng chúng tôi chinh phục những thử thách trong môn Toán nhé!