Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 trong sách giáo khoa. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, đặc biệt là với những bài toán phức tạp.
Trang 59 và 60 SGK Toán 8 chứa đựng những bài tập quan trọng, giúp củng cố kiến thức về các chủ đề đã học.
Hãy cùng giaitoan.edu.vn khám phá và chinh phục những bài toán này một cách hiệu quả nhất!
Cắt \(\Delta A'B'C'\) và \(\Delta ABC\) bằng giấy có \(\widehat {A'} = \widehat A\) và \(\widehat {B'} = \widehat B\).
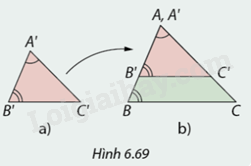
Cắt \(\Delta A'B'C'\) và \(\Delta ABC\) bằng giấy có \(\widehat {A'} = \widehat A\) và \(\widehat {B'} = \widehat B\). Xếp \(\Delta A'B'C'\) lên \(\Delta ABC\) sao cho cạnh \(A'B'\) chồng lên cạnh \(AB\) và cạnh \(A'C'\) chồng lên cạnh \(AC\) như Hình 6.69.
1. Vì sao trong Hình 6.69b, cạnh \(B'C'\) song song với cạnh \(BC\)
2. Hãy đưa ra kết luận về \(\Delta A'B'C'\) và \(\Delta ABC\).
Phương pháp giải:
Dựa vào tính chất hai đường thẳng song song để chứng minh cạnh \(B'C'\) song song với cạnh \(BC\), sau đó nhận xét về \(\Delta A'B'C'\) và \(\Delta ABC\).
Lời giải chi tiết:
1. Ta có:
\(\widehat {A'B'C'} = \widehat {ABC}\) (gt)
Mà hai góc này ở vị trí so le trong
=> \(B'C'//BC\).
2. Áp dụng định lý học ở bài 4, ta có:
\(\Delta A'B'C'\)∽\(\Delta ABC\).
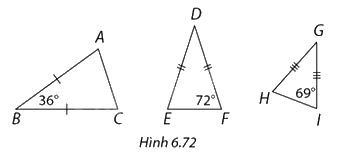
Chỉ ra cặp tam giác đồng dạng trong Hình 6.72.
Phương pháp giải:
Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết:
Xét tam giác cân \(ABC\), ta có:
\(\widehat A = \widehat C = \frac{{180^\circ - \widehat B}}{2} = \frac{{180^\circ - 36^\circ }}{2} = 72^\circ \)
Xét tam giác cân \(DEF\), ta có:
\(\begin{array}{l}\widehat E = \widehat F = 72^\circ \\\widehat D = 180^\circ - \left( {\widehat E + \widehat F} \right) = 180^\circ - \left( {72^\circ + 72^\circ } \right) = 36^\circ \end{array}\)
Xét tam giác cân \(GHI\), ta có:
\(\begin{array}{l}\widehat H = \widehat I = 69^\circ \\\widehat G = \frac{{180^\circ - \left( {\widehat H + \widehat I} \right)}}{2} = \frac{{180^\circ - \left( {69^\circ + 69^\circ } \right)}}{2} = 21^\circ \end{array}\)
Ta thấy tam giác \(ABC\) và tam giác \(EDF\) có:
\(\begin{array}{l}\widehat A = \widehat F = 72^\circ \\\widehat B = \widehat D = 36^\circ \end{array}\)
=> \(\Delta ABC\)∽\(\Delta EDF\) (g-g)
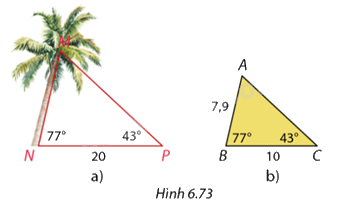
Trong Hình 6.73a, đỉnh \(\left( M \right)\), gốc \(\left( N \right)\) của cây dừa và vị trí bạn Phương đứng \(\left( P \right)\) tạo thành tam giác \(MNP\). Phương đo được \(\widehat N = 77^\circ ,\widehat P = 43^\circ \) và \(NP = 20m\). Phương vẽ tam giác \(ABC\) có \(\widehat B = 77^\circ ,\widehat C = 43^\circ \) và \(BC = 10cm\) (Hình 6.73b), đo độ dài cạnh \(AB\) và từ đó tính chiều cao \(MN\) của cây dừa. Em hãy giải thích cách làm của Phương và tính chiều cao \(MN\) của cây dừa nếu \(AB = 7,9cm\)
Phương pháp giải:
Dựa vào trường hợp đồng dạng góc góc: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết:
Xét tam giác \(MNP\) và tam giác \(ABC\) ta có:
\(\begin{array}{l}\widehat N = \widehat B = 77^\circ \\\widehat P = \widehat C = 43^\circ \end{array}\)
=>\(\Delta MNP\)∽\(\Delta ABC\) (g-g)
Ta có tỉ số đồng dạng:
\(\begin{array}{l}\frac{{MN}}{{AB}} = \frac{{NP}}{{BC}} = \frac{{MP}}{{AC}}\\ \Leftrightarrow \frac{{MN}}{{7,9}} = \frac{{20}}{{10}}\\ \Rightarrow MN = 15,8\end{array}\)
Vậy chiều cao của cây dừa là 15,8 m.
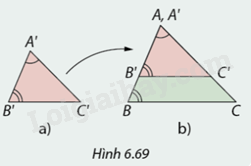
Cắt \(\Delta A'B'C'\) và \(\Delta ABC\) bằng giấy có \(\widehat {A'} = \widehat A\) và \(\widehat {B'} = \widehat B\). Xếp \(\Delta A'B'C'\) lên \(\Delta ABC\) sao cho cạnh \(A'B'\) chồng lên cạnh \(AB\) và cạnh \(A'C'\) chồng lên cạnh \(AC\) như Hình 6.69.
1. Vì sao trong Hình 6.69b, cạnh \(B'C'\) song song với cạnh \(BC\)
2. Hãy đưa ra kết luận về \(\Delta A'B'C'\) và \(\Delta ABC\).
Phương pháp giải:
Dựa vào tính chất hai đường thẳng song song để chứng minh cạnh \(B'C'\) song song với cạnh \(BC\), sau đó nhận xét về \(\Delta A'B'C'\) và \(\Delta ABC\).
Lời giải chi tiết:
1. Ta có:
\(\widehat {A'B'C'} = \widehat {ABC}\) (gt)
Mà hai góc này ở vị trí so le trong
=> \(B'C'//BC\).
2. Áp dụng định lý học ở bài 4, ta có:
\(\Delta A'B'C'\)∽\(\Delta ABC\).
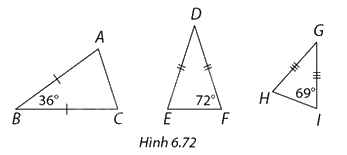
Chỉ ra cặp tam giác đồng dạng trong Hình 6.72.
Phương pháp giải:
Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết:
Xét tam giác cân \(ABC\), ta có:
\(\widehat A = \widehat C = \frac{{180^\circ - \widehat B}}{2} = \frac{{180^\circ - 36^\circ }}{2} = 72^\circ \)
Xét tam giác cân \(DEF\), ta có:
\(\begin{array}{l}\widehat E = \widehat F = 72^\circ \\\widehat D = 180^\circ - \left( {\widehat E + \widehat F} \right) = 180^\circ - \left( {72^\circ + 72^\circ } \right) = 36^\circ \end{array}\)
Xét tam giác cân \(GHI\), ta có:
\(\begin{array}{l}\widehat H = \widehat I = 69^\circ \\\widehat G = \frac{{180^\circ - \left( {\widehat H + \widehat I} \right)}}{2} = \frac{{180^\circ - \left( {69^\circ + 69^\circ } \right)}}{2} = 21^\circ \end{array}\)
Ta thấy tam giác \(ABC\) và tam giác \(EDF\) có:
\(\begin{array}{l}\widehat A = \widehat F = 72^\circ \\\widehat B = \widehat D = 36^\circ \end{array}\)
=> \(\Delta ABC\)∽\(\Delta EDF\) (g-g)
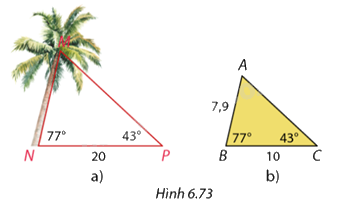
Trong Hình 6.73a, đỉnh \(\left( M \right)\), gốc \(\left( N \right)\) của cây dừa và vị trí bạn Phương đứng \(\left( P \right)\) tạo thành tam giác \(MNP\). Phương đo được \(\widehat N = 77^\circ ,\widehat P = 43^\circ \) và \(NP = 20m\). Phương vẽ tam giác \(ABC\) có \(\widehat B = 77^\circ ,\widehat C = 43^\circ \) và \(BC = 10cm\) (Hình 6.73b), đo độ dài cạnh \(AB\) và từ đó tính chiều cao \(MN\) của cây dừa. Em hãy giải thích cách làm của Phương và tính chiều cao \(MN\) của cây dừa nếu \(AB = 7,9cm\)
Phương pháp giải:
Dựa vào trường hợp đồng dạng góc góc: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết:
Xét tam giác \(MNP\) và tam giác \(ABC\) ta có:
\(\begin{array}{l}\widehat N = \widehat B = 77^\circ \\\widehat P = \widehat C = 43^\circ \end{array}\)
=>\(\Delta MNP\)∽\(\Delta ABC\) (g-g)
Ta có tỉ số đồng dạng:
\(\begin{array}{l}\frac{{MN}}{{AB}} = \frac{{NP}}{{BC}} = \frac{{MP}}{{AC}}\\ \Leftrightarrow \frac{{MN}}{{7,9}} = \frac{{20}}{{10}}\\ \Rightarrow MN = 15,8\end{array}\)
Vậy chiều cao của cây dừa là 15,8 m.
Trang 59 và 60 của sách giáo khoa Toán 8 thường tập trung vào các dạng bài tập liên quan đến các kiến thức đã được học trong chương. Để giải quyết hiệu quả các bài tập này, học sinh cần nắm vững lý thuyết, hiểu rõ các định nghĩa và công thức liên quan.
Thông thường, trang 59 và 60 sẽ chứa các bài tập về:
Để giúp học sinh hiểu rõ hơn về cách giải các bài tập trên trang 59 và 60, chúng ta sẽ đi vào phân tích từng bài tập cụ thể:
Giả sử bài tập yêu cầu thực hiện phép cộng hai đa thức: (3x2 + 2x - 1) + (x2 - 5x + 3)
Kết quả: 4x2 - 3x + 2
Giả sử bài tập yêu cầu phân tích đa thức thành nhân tử: x2 - 4
Áp dụng hằng đẳng thức a2 - b2 = (a - b)(a + b), ta có:
x2 - 4 = (x - 2)(x + 2)
Việc giải bài tập Toán 8 không chỉ giúp học sinh củng cố kiến thức mà còn rèn luyện tư duy logic, khả năng giải quyết vấn đề và kỹ năng tính toán. Đây là những kỹ năng quan trọng không chỉ trong học tập mà còn trong cuộc sống.
Giaitoan.edu.vn cam kết cung cấp cho bạn những lời giải chi tiết, dễ hiểu và chính xác nhất. Chúng tôi luôn cập nhật những bài tập mới nhất và đa dạng nhất để đáp ứng nhu cầu học tập của bạn. Hãy truy cập giaitoan.edu.vn ngay hôm nay để khám phá thế giới Toán học đầy thú vị!
| Công thức | Mô tả |
|---|---|
| a2 - b2 = (a - b)(a + b) | Hằng đẳng thức hiệu hai bình phương |
| (a + b)2 = a2 + 2ab + b2 | Hằng đẳng thức bình phương của một tổng |
| (a - b)2 = a2 - 2ab + b2 | Hằng đẳng thức bình phương của một hiệu |
Hy vọng với những hướng dẫn và lời giải chi tiết trên, bạn sẽ tự tin hơn trong việc giải các bài tập Toán 8 trang 59 và 60. Chúc bạn học tập tốt!