Chào mừng bạn đến với bài học về Lý thuyết Các trường hợp đồng dạng của hai tam giác vuông trong chương trình Toán 8. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về chủ đề này, giúp bạn giải quyết các bài tập một cách hiệu quả.
Tại giaitoan.edu.vn, chúng tôi luôn cố gắng mang đến những bài giảng chất lượng, dễ hiểu và phù hợp với mọi đối tượng học sinh.
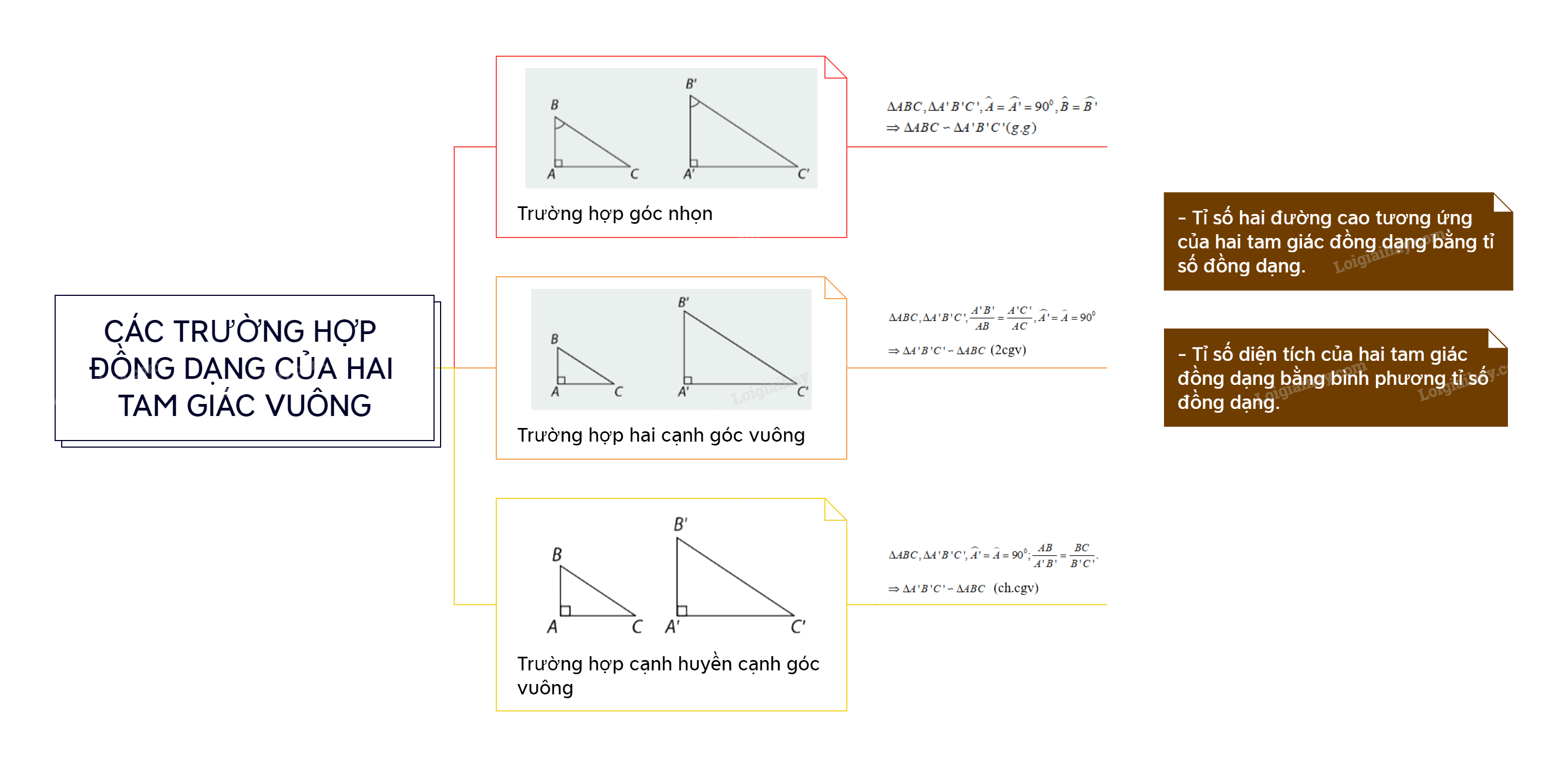
Các trường hợp đồng dạng của hai tam giác vuông là gì?
1. Trường hợp góc nhọn
Nếu tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
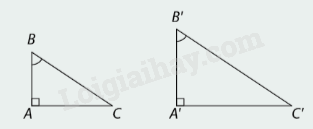
\(\begin{array}{l}\Delta ABC,\Delta A'B'C',\widehat A = \widehat {A'} = {90^0},\widehat B = \widehat {B'}\\ \Rightarrow \Delta ABC \backsim \Delta A'B'C'\,(g.g)\end{array}\)
2. Trường hợp hai cạnh góc vuông
Nếu tam giác vuông này có hai cạnh góc vuông tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
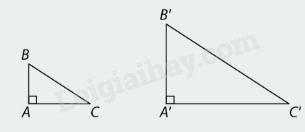
\(\Delta ABC,\Delta A'B'C',\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}},\widehat {A'} = \widehat A = {90^0}\)
\( \Rightarrow \Delta A'B'C' \backsim \Delta ABC\,\)(2cgv)
3. Trường hợp cạnh huyền cạnh góc vuông
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng
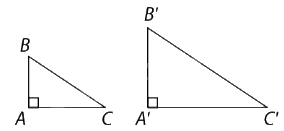
\(\Delta ABC,\Delta A'B'C',\widehat {A'} = \widehat A = {90^0};\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}.\)
\( \Rightarrow \Delta A'B'C' \backsim \Delta ABC\,\) (ch.cgv)
Chú ý:
- Tỉ số hai đường cao tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng.
- Tỉ số diện tích của hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng.
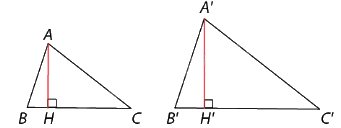
Nếu với tỉ số đồng dạng k thì \(\frac{{A'H'}}{{AH}} = k\) và \(\frac{{{S_{A'B'C'}}}}{{{S_{ABC}}}} = {k^2}\)
Trong chương trình Toán 8, kiến thức về tam giác đồng dạng đóng vai trò vô cùng quan trọng. Đặc biệt, việc nắm vững lý thuyết các trường hợp đồng dạng của hai tam giác vuông là nền tảng để giải quyết nhiều bài toán hình học phức tạp. Bài viết này sẽ đi sâu vào phân tích các trường hợp đồng dạng, cung cấp ví dụ minh họa và bài tập thực hành để giúp bạn hiểu rõ hơn về chủ đề này.
Hai tam giác được gọi là đồng dạng nếu chúng có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ. Kí hiệu: △ABC ~ △A'B'C'.
Có ba trường hợp đồng dạng của hai tam giác vuông:
Nếu △ABC vuông tại A và △A'B'C' vuông tại A' có ∠B = ∠B' thì △ABC ~ △A'B'C'.
Ví dụ: Cho △ABC vuông tại A, ∠B = 60° và △A'B'C' vuông tại A', ∠B' = 60°. Chứng minh △ABC ~ △A'B'C'.
Nếu △ABC vuông tại A và △A'B'C' vuông tại A' có AB/A'B' = AC/A'C' thì △ABC ~ △A'B'C'.
Ví dụ: Cho △ABC vuông tại A, AB = 3cm, AC = 4cm và △A'B'C' vuông tại A', A'B' = 6cm, A'C' = 8cm. Chứng minh △ABC ~ △A'B'C'.
Nếu △ABC vuông tại A và △A'B'C' vuông tại A' có BC/B'C' = AB/A'B' thì △ABC ~ △A'B'C'.
Ví dụ: Cho △ABC vuông tại A, BC = 5cm, AB = 3cm và △A'B'C' vuông tại A', B'C' = 10cm, A'B' = 6cm. Chứng minh △ABC ~ △A'B'C'.
Các trường hợp đồng dạng của hai tam giác vuông được ứng dụng rộng rãi trong việc giải các bài toán liên quan đến:
Bài 1: Cho △ABC vuông tại A, có AB = 6cm, AC = 8cm. Gọi D là điểm trên BC sao cho BD = 2cm. Chứng minh △ABD ~ △CBA.
Bài 2: Cho △ABC vuông tại A, đường cao AH. Chứng minh △ABH ~ △CBA.
Bài 3: Một người đứng ở vị trí A, nhìn thấy đỉnh của một tòa nhà cao 20m dưới góc 60°. Sau đó, người đó đi thêm 10m nữa theo phương ngang đến vị trí B, lại nhìn thấy đỉnh của tòa nhà đó dưới góc 30°. Tính chiều cao của tòa nhà.
Khi áp dụng các trường hợp đồng dạng, cần chú ý:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về lý thuyết các trường hợp đồng dạng của hai tam giác vuông. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng vào giải các bài tập một cách hiệu quả. Chúc bạn học tốt!