Chào mừng các em học sinh đến với bài giải chi tiết mục 1 trang 43 SGK Toán 8 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp cho các em lời giải đầy đủ, dễ hiểu, giúp các em hiểu rõ hơn về kiến thức và phương pháp giải bài tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng cao, hỗ trợ các em học tập tốt hơn. Hãy cùng bắt đầu khám phá bài giải ngay bây giờ!
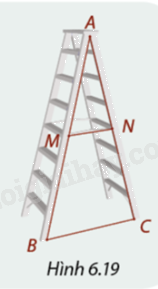
Trong Hình 6.19, để thang xếp đứng vững, hai chân \(AB\) và \(AC\) của nó được nối với
Trong Hình 6.19, để thang xếp đứng vững, hai chân \(AB\) và \(AC\) của nó được nối với nhau bằng thanh khóa \(MN.\) So sánh các đoạn thẳng \(AM\) và \(BN,AN\) và \(CN,\) em có nhận xét gì về vị trí điểm \(M\) và \(N\) trên cạnh \(AB\) và \(AC\) của tam giác \(ABC?\)
Phương pháp giải:
So sánh các đoạn thẳng \(AM\) và \(BN,AN\) và \(CN,\) nêu nhận xét về vị trí điểm \(M\) và \(N\) trên cạnh \(AB\) và \(AC\) của tam giác \(ABC.\)
Lời giải chi tiết:
Ta thấy \(AM = MB;AN = NC.\)
Hay điểm \(M\) là trung điểm cạnh \(AB\) và \(N\) là trung điểm cạnh \(AC.\)
Vẽ tam giác \(MNP\) bất kì và vẽ các đường trung bình của nó.
Phương pháp giải:
Vẽ tam giác \(MNP\) lấy \(A,B,C\) lần lượt là trung điểm của \(MN,NP,MP.\)
Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Lời giải chi tiết:
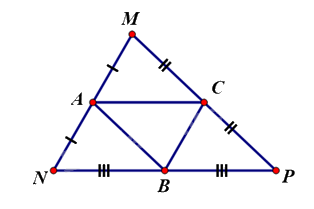
Lấy \(A,B,C\) lần lượt là trung điểm của \(MN,NP,MP.\)
Suy ra \(AC,BC,AC\) là các đường trung bình của tam giác \(MNP.\)
Trong Hình 6.19, để thang xếp đứng vững, hai chân \(AB\) và \(AC\) của nó được nối với nhau bằng thanh khóa \(MN.\) So sánh các đoạn thẳng \(AM\) và \(BN,AN\) và \(CN,\) em có nhận xét gì về vị trí điểm \(M\) và \(N\) trên cạnh \(AB\) và \(AC\) của tam giác \(ABC?\)
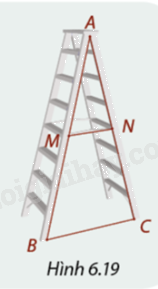
Phương pháp giải:
So sánh các đoạn thẳng \(AM\) và \(BN,AN\) và \(CN,\) nêu nhận xét về vị trí điểm \(M\) và \(N\) trên cạnh \(AB\) và \(AC\) của tam giác \(ABC.\)
Lời giải chi tiết:
Ta thấy \(AM = MB;AN = NC.\)
Hay điểm \(M\) là trung điểm cạnh \(AB\) và \(N\) là trung điểm cạnh \(AC.\)
Vẽ tam giác \(MNP\) bất kì và vẽ các đường trung bình của nó.
Phương pháp giải:
Vẽ tam giác \(MNP\) lấy \(A,B,C\) lần lượt là trung điểm của \(MN,NP,MP.\)
Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Lời giải chi tiết:
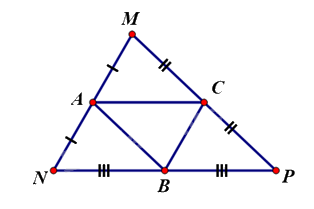
Lấy \(A,B,C\) lần lượt là trung điểm của \(MN,NP,MP.\)
Suy ra \(AC,BC,AC\) là các đường trung bình của tam giác \(MNP.\)
Mục 1 trang 43 SGK Toán 8 thường xoay quanh các kiến thức về hình học, cụ thể là các định lý và tính chất liên quan đến tứ giác. Để giải quyết các bài tập trong mục này, học sinh cần nắm vững các khái niệm cơ bản như:
Dưới đây là một số bài tập điển hình thường gặp trong mục 1 trang 43 SGK Toán 8 và hướng dẫn giải chi tiết:
Để chứng minh một tứ giác là hình bình hành, ta có thể sử dụng một trong các cách sau:
Ví dụ: Cho tứ giác ABCD có AB song song CD và AD song song BC. Chứng minh ABCD là hình bình hành.
Giải: Vì AB song song CD và AD song song BC nên tứ giác ABCD là hình bình hành (dấu hiệu nhận biết hình bình hành).
Trong hình bình hành, các góc đối bằng nhau và các góc kề bù có tổng bằng 180 độ. Để tính các góc của hình bình hành, ta có thể sử dụng các tính chất này.
Ví dụ: Cho hình bình hành ABCD có góc A bằng 60 độ. Tính các góc còn lại.
Giải:
Trong hình thoi, bốn cạnh bằng nhau. Để tính độ dài các cạnh của hình thoi, ta có thể sử dụng các tính chất của hình thoi và các định lý liên quan.
Khi giải các bài tập về tứ giác, học sinh cần lưu ý những điều sau:
Kiến thức về tứ giác có ứng dụng rất lớn trong thực tế, đặc biệt trong các lĩnh vực như kiến trúc, xây dựng, thiết kế và kỹ thuật. Việc hiểu rõ về các loại tứ giác và tính chất của chúng giúp chúng ta giải quyết các vấn đề thực tế một cách hiệu quả hơn.
Hy vọng với bài giải chi tiết và hướng dẫn cụ thể trên, các em học sinh đã nắm vững kiến thức và phương pháp giải các bài tập trong mục 1 trang 43 SGK Toán 8. Chúc các em học tập tốt và đạt kết quả cao!
| Loại Tứ Giác | Tính Chất Chính |
|---|---|
| Hình Bình Hành | Hai cặp cạnh đối song song, hai cặp cạnh đối bằng nhau, hai đường chéo cắt nhau tại trung điểm của mỗi đường. |
| Hình Chữ Nhật | Có bốn góc vuông, hai đường chéo bằng nhau. |
| Hình Thoi | Bốn cạnh bằng nhau, hai đường chéo vuông góc với nhau. |
| Hình Vuông | Có bốn cạnh bằng nhau và bốn góc vuông. |