Phương trình bậc nhất một ẩn là một trong những kiến thức cơ bản và quan trọng trong chương trình Toán 8. Việc nắm vững lý thuyết và kỹ năng giải phương trình này không chỉ giúp học sinh đạt kết quả tốt trong các bài kiểm tra mà còn là nền tảng vững chắc cho các kiến thức toán học nâng cao hơn.
Tại giaitoan.edu.vn, chúng tôi cung cấp tài liệu học tập đầy đủ, dễ hiểu về Lý thuyết Phương trình bậc nhất một ẩn và cách giải SGK Toán 8, giúp bạn tự tin chinh phục môn Toán.
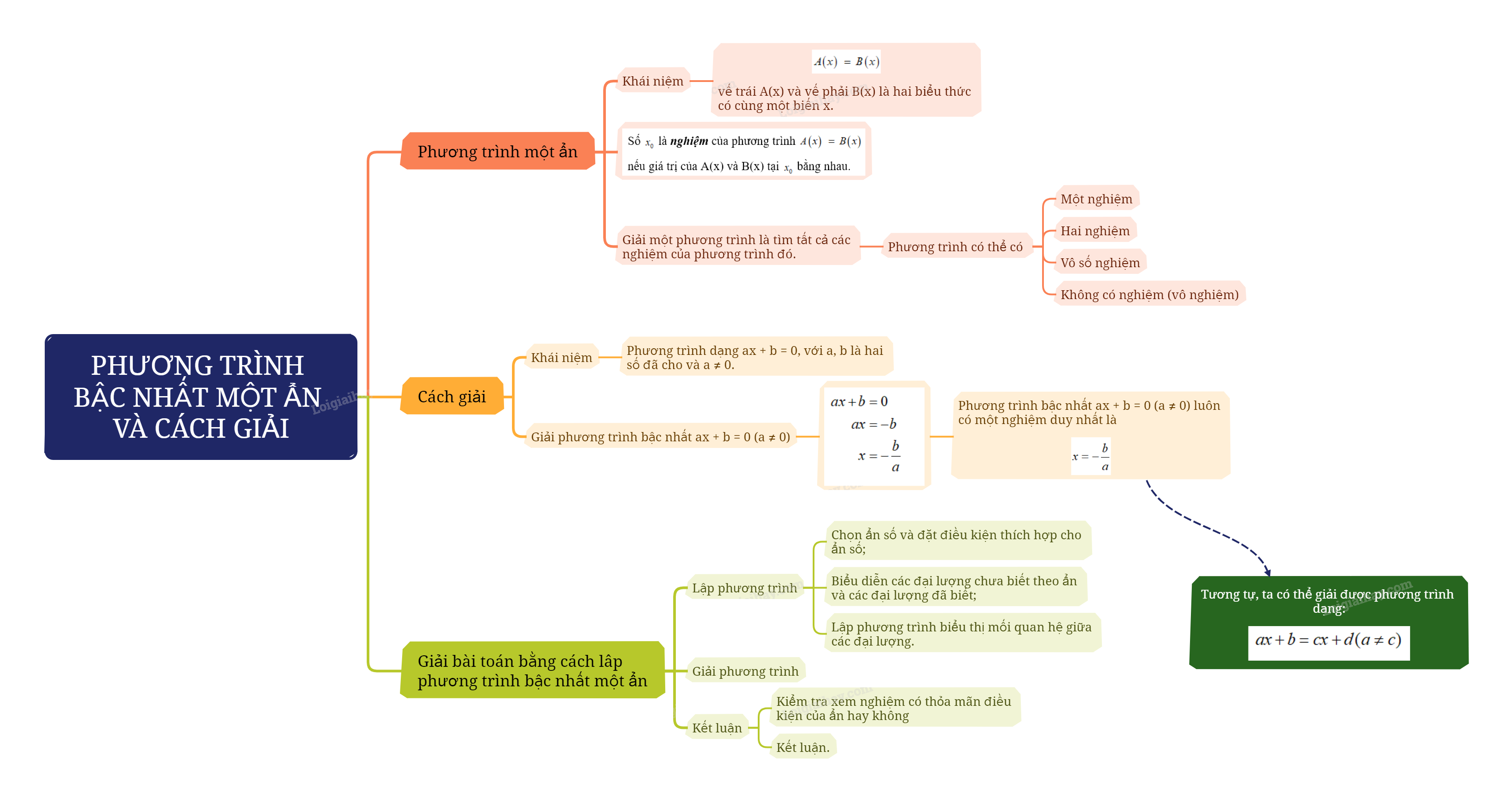
Phương trình là gì?
1. Phương trình
Cho A(x), B(x) là hai biểu thức của biến x. Khi cần tìm x sao cho A(x) = B(x) thì ta nói A(x) = B(x) là một phương trình với ẩn x, A(x) là về trái, B(x) là vế phải của phương trình.
Ví dụ: \(3x--1 = 2x + 3;3x = 5\) là các phương trình ẩn x.
Số \({x_0}\) là nghiệm của phương trình \(A\left( x \right) = B\left( x \right)\)nếu giá trị của A(x) và B(x) tại \({x_0}\) bằng nhau.
Ví dụ: \(x = 2\) là nghiệm của phương trình \(2x = x + 2\) vì thay \(x = 2\) vào phương trình, ta được 2.2 = 2 + 2
Giải một phương trình là tìm tất cả các nghiệm của phương trình đó.
Một phương trình có thể có một nghiệm, hai nghiệm,… nhưng cũng có thể không có nghiệm nào hoặc vô số nghiệm. Phương trình không có nghiệm nào được gọi là phương trình vô nghiệm.
Ví dụ: Giải phương trình: \(3x + 6 = 0\)
Ta có: \(3x + 6 = 0 \Leftrightarrow 3x = - 6 \Leftrightarrow x = - 2\)
Vậy tập nghiệm của phương trình là S = {-2}
2. Phương trình bậc nhất một ẩn và cách giải
Khái niệm: Phương trình dạng ax + b = 0, với a, b là hai số đã cho và \(a \ne 0\), được gọi là phương trình bậc nhất một ẩn (ẩn số là x).
Cách giải:
Phương trình bậc nhất ax + b = 0 (\(a \ne 0\)) được giải như sau:
\(\begin{array}{c}ax + b = 0\\ax = - b\\x = - \frac{b}{a}\end{array}\)
Phương trình bậc nhất ax + b = 0 (\(a \ne 0\)) luôn có một nghiệm duy nhất là \(x = - \frac{b}{a}\).
Ví dụ: Giải phương trình: \(3x + 11 = 0\)
Ta có:
\(\begin{array}{c}3x + 11 = 0\\3x = - 11\\x = - \frac{{11}}{3}\end{array}\)
Vậy phương trình có một nghiệm duy nhất \(x = - \frac{{11}}{3}\).
Nhận xét: Bằng cách tương tự như trên, ta có thể giải được phương trình dạng:
\(ax + b = cx + d(a \ne c)\)
Ví dụ: Giải phương trình: \(7x--\left( {2x + 3} \right) = 5\left( {x--2} \right)\)
\(\begin{array}{c}11x--\left( {2x + 3} \right) = {\rm{ 6}}\left( {x--2} \right)\\11x - 2x - 3 = 6x - 12\\11x - 2x - 6x = - 12 + 3\\3x = - 9\\x = \frac{{ - 9}}{3}\\x = - 3\end{array}\)
Vậy nghiệm của phương trình là x = -3.
Lưu ý: Quá trình giải các phương trình có thể dẫn đến trường hợp đặc biệt là hệ số của ẩn bằng 0. Khi đó phương trình có thể vô nghiệm hoặc nghiệm đúng với mọi x.
3. Giải bài toán bằng cách lập phương trình bậc nhất một ẩn
Bước 1. Lập phương trình.
- Chọn ẩn số và đặt điều kiện cho ẩn số.
- Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.
- Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2. Giải phương trình.
Bước 3. Kiểm tra xem nghiệm có thỏa mãn điều kiện của ẩn hay không rồi kết luận.
Phương trình bậc nhất một ẩn là phương trình có dạng ax + b = 0, trong đó x là ẩn số, a và b là các hệ số với a ≠ 0. Hiểu rõ định nghĩa này là bước đầu tiên để làm quen với loại phương trình này.
Để hiểu rõ hơn về phương trình bậc nhất một ẩn, chúng ta cần nắm vững các khái niệm sau:
Phương trình bậc nhất một ẩn có thể xuất hiện ở nhiều dạng khác nhau, nhưng đều có thể được đưa về dạng ax + b = 0. Một số dạng phổ biến bao gồm:
Để giải phương trình bậc nhất một ẩn, chúng ta thực hiện theo các bước sau:
Ví dụ 1: Giải phương trình 2x + 5 = 11
Ví dụ 2: Giải phương trình 3(x - 2) = 9
Để củng cố kiến thức, hãy thử giải các bài tập sau:
Khi giải phương trình bậc nhất một ẩn, cần lưu ý:
Hy vọng với những kiến thức và ví dụ trên, bạn đã hiểu rõ hơn về Lý thuyết Phương trình bậc nhất một ẩn và cách giải SGK Toán 8. Hãy luyện tập thường xuyên để nâng cao kỹ năng giải toán của mình!