Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8 trong sách giáo khoa. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Với mục tiêu giúp học sinh nắm vững kiến thức và tự tin hơn trong học tập, chúng tôi đã biên soạn bộ giải bài tập Toán 8 trang 99, 100 SGK một cách cẩn thận và đầy đủ.
Hãy cùng khám phá lời giải chi tiết và phương pháp giải bài tập hiệu quả ngay sau đây!
Dùng một “phễu đong” dạng hình chóp tam giác đều với cạnh đáy dài
Tính độ dài cạnh đáy của một hình chóp tứ giác đều, biết thể tích của hình chóp bằng \(13,5c{m^3}\) và chiều cao của hình chóp bằng \(4,5cm.\)
Phương pháp giải:
Áp dụng công thức tính thể tích hình chóp tứ giác đều:
\(V = \frac{1}{3}S.h\)
Với \(S\) là diện tích đáy và \(h\) là chiều cao của hình chóp đó.
Sau đó tính độ dài cạnh đáy.
Lời giải chi tiết:
Ta có:
\(V = \frac{1}{3}S.h\\13,5 = \frac{1}{3}.S.4,5 \\13,5 = 1,5.S\)
Diện tích đáy của hình chóp tứ giác đều đó là:
\( S = \frac{13,5}{1,5} = 9c{m^2}\)
Gọi a là độ dài cạnh đáy của hình chóp tứ giác đều.
Độ dài cạnh đáy của hình chóp tứ giác đều là:
\(S = a.a\\9 = {a^2}\)
Do đó \(a = \sqrt 9 = 3cm\)
Tính thể tích hình chóp tứ giác đều trong Hình 4.29, biết \(So = 6cm,AB = 5cm.\)
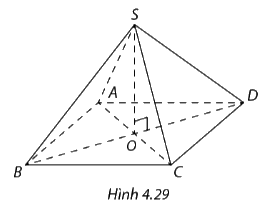
Phương pháp giải:
Áp dụng công thức tính thể tích hình chóp tứ giác đều:
\(V = \frac{1}{3}S.h\)
Với \(S\) là diện tích đáy và \(h\) là chiều cao của hình chóp đó.
Lời giải chi tiết:
Thể tích hình chóp tứ giác đều đó là:
\(V = \frac{1}{3}S.h = \frac{1}{3}.5.6 = 10c{m^3}\)
Dùng một “phễu đong” dạng hình chóp tam giác đều với cạnh đáy dài \(12cm\) và chiều cao bằng \(4cm\) (Hình 4.28a) đong các hạt đỗ đến ngang miệng rồi đổ vào một hộp có dạng hình lăng trụ đứng tam giác với đáy là tam giác đều cạnh \(12cm\) và chiều cao bằng \(4cm\) (Hình 4.28b). Cần đong bao nhiêu lần như vậy để đổ đầy hộp?
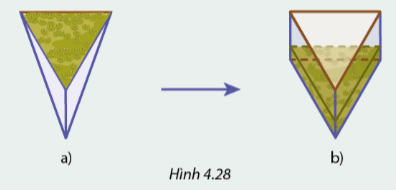
Phương pháp giải:
Dùng phễu đong hình chóp tam giác đều đong các hạt đỗ đến ngang miệng rồi đổ vào một hộp có dạng hình lăng trụ đứng tam giác với đáy là tam giác đều.
Lời giải chi tiết:
Cần đong 3 lần như vậy để đổ đầy hộp.
Kim tự tháp Cheops ở Ai Cập được xây dựng vào khoảng 2 500 năm trước công nguyên.
a) Kim tự tháp này có dạng hình chóp tứ giác đều với chiều cao \(147m,\) cạnh đáy dài \(230m.\) hãy tính thể tích của nó.
b) Hiện nay, kim tự tháp này vẫn có dạng hình chóp tứ giác đều với chiều cao khoảng \(138m,\) còn độ dài cạnh đáy vẫn khoảng \(230m.\) Thể tích của kim tự tháp giảm bao nhiêu mét khối so với khi mới xây dựng?

Phương pháp giải:
Áp dụng công thức tính thể tích hình chóp tứ giác đều:
\(V = \frac{1}{3}S.h\)
Với \(S\) là diện tích đáy và \(h\) là chiều cao của hình chóp đó.
Lời giải chi tiết:
a) Thể tích của kim tự tháp Cheops là:
\(V = \frac{1}{3}S.h = \frac{1}{3}.230.230.147 = 2592100({m^3})\)
b) Thể tích của kim tự tháp hiện nay là:
\(V = \frac{1}{3}S.h = \frac{1}{3}.138.230.230 = 2433400({m^3})\)
Thể tích của kim tự tháp giảm số mét khối so với khi mới xây dựng là:
\(2592100 - 2433400 = 158700({m^3})\)
Dùng một “phễu đong” dạng hình chóp tam giác đều với cạnh đáy dài \(12cm\) và chiều cao bằng \(4cm\) (Hình 4.28a) đong các hạt đỗ đến ngang miệng rồi đổ vào một hộp có dạng hình lăng trụ đứng tam giác với đáy là tam giác đều cạnh \(12cm\) và chiều cao bằng \(4cm\) (Hình 4.28b). Cần đong bao nhiêu lần như vậy để đổ đầy hộp?
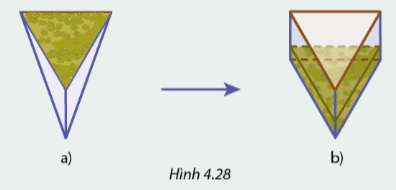
Phương pháp giải:
Dùng phễu đong hình chóp tam giác đều đong các hạt đỗ đến ngang miệng rồi đổ vào một hộp có dạng hình lăng trụ đứng tam giác với đáy là tam giác đều.
Lời giải chi tiết:
Cần đong 3 lần như vậy để đổ đầy hộp.
Tính thể tích hình chóp tứ giác đều trong Hình 4.29, biết \(So = 6cm,AB = 5cm.\)
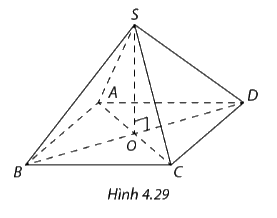
Phương pháp giải:
Áp dụng công thức tính thể tích hình chóp tứ giác đều:
\(V = \frac{1}{3}S.h\)
Với \(S\) là diện tích đáy và \(h\) là chiều cao của hình chóp đó.
Lời giải chi tiết:
Thể tích hình chóp tứ giác đều đó là:
\(V = \frac{1}{3}S.h = \frac{1}{3}.5.6 = 10c{m^3}\)
Tính độ dài cạnh đáy của một hình chóp tứ giác đều, biết thể tích của hình chóp bằng \(13,5c{m^3}\) và chiều cao của hình chóp bằng \(4,5cm.\)
Phương pháp giải:
Áp dụng công thức tính thể tích hình chóp tứ giác đều:
\(V = \frac{1}{3}S.h\)
Với \(S\) là diện tích đáy và \(h\) là chiều cao của hình chóp đó.
Sau đó tính độ dài cạnh đáy.
Lời giải chi tiết:
Ta có:
\(V = \frac{1}{3}S.h\\13,5 = \frac{1}{3}.S.4,5 \\13,5 = 1,5.S\)
Diện tích đáy của hình chóp tứ giác đều đó là:
\( S = \frac{13,5}{1,5} = 9c{m^2}\)
Gọi a là độ dài cạnh đáy của hình chóp tứ giác đều.
Độ dài cạnh đáy của hình chóp tứ giác đều là:
\(S = a.a\\9 = {a^2}\)
Do đó \(a = \sqrt 9 = 3cm\)
Kim tự tháp Cheops ở Ai Cập được xây dựng vào khoảng 2 500 năm trước công nguyên.
a) Kim tự tháp này có dạng hình chóp tứ giác đều với chiều cao \(147m,\) cạnh đáy dài \(230m.\) hãy tính thể tích của nó.
b) Hiện nay, kim tự tháp này vẫn có dạng hình chóp tứ giác đều với chiều cao khoảng \(138m,\) còn độ dài cạnh đáy vẫn khoảng \(230m.\) Thể tích của kim tự tháp giảm bao nhiêu mét khối so với khi mới xây dựng?

Phương pháp giải:
Áp dụng công thức tính thể tích hình chóp tứ giác đều:
\(V = \frac{1}{3}S.h\)
Với \(S\) là diện tích đáy và \(h\) là chiều cao của hình chóp đó.
Lời giải chi tiết:
a) Thể tích của kim tự tháp Cheops là:
\(V = \frac{1}{3}S.h = \frac{1}{3}.230.230.147 = 2592100({m^3})\)
b) Thể tích của kim tự tháp hiện nay là:
\(V = \frac{1}{3}S.h = \frac{1}{3}.138.230.230 = 2433400({m^3})\)
Thể tích của kim tự tháp giảm số mét khối so với khi mới xây dựng là:
\(2592100 - 2433400 = 158700({m^3})\)
Trang 99 và 100 sách giáo khoa Toán 8 thường chứa các bài tập liên quan đến các kiến thức đã học trong chương. Để giải quyết hiệu quả các bài tập này, học sinh cần nắm vững lý thuyết, hiểu rõ các định nghĩa, tính chất và công thức liên quan.
Bài tập này thường yêu cầu học sinh vận dụng kiến thức về hình học, cụ thể là các tính chất của hình thang cân. Để giải bài tập này, bạn cần:
Ví dụ, nếu bài tập yêu cầu tính độ dài đường trung bình của hình thang cân, bạn có thể sử dụng công thức: Đường trung bình = (đáy lớn + đáy bé) / 2.
Bài tập này có thể liên quan đến việc chứng minh một đẳng thức hình học. Để giải bài tập này, bạn cần:
Ví dụ, để chứng minh hai tam giác bằng nhau, bạn có thể sử dụng các trường hợp bằng nhau của tam giác (cạnh - cạnh - cạnh, cạnh - góc - cạnh, góc - cạnh - góc).
Bài tập này có thể yêu cầu học sinh giải một bài toán thực tế liên quan đến toán học. Để giải bài tập này, bạn cần:
Ví dụ, nếu bài toán yêu cầu tính diện tích một mảnh đất hình chữ nhật, bạn cần biết chiều dài và chiều rộng của mảnh đất, sau đó sử dụng công thức: Diện tích = chiều dài x chiều rộng.
Giaitoan.edu.vn không chỉ cung cấp lời giải chi tiết cho các bài tập trong SGK mà còn cung cấp nhiều tài liệu học tập hữu ích khác, như:
Chúng tôi hy vọng rằng với sự hỗ trợ của giaitoan.edu.vn, bạn sẽ học tập môn Toán 8 một cách hiệu quả và đạt được kết quả tốt nhất.
| Công thức | Mô tả |
|---|---|
| Đường trung bình của hình thang | (đáy lớn + đáy bé) / 2 |
| Diện tích hình chữ nhật | Chiều dài x Chiều rộng |
Hãy nhớ rằng, việc học toán không chỉ là việc giải bài tập mà còn là việc hiểu rõ bản chất của vấn đề. Hãy dành thời gian suy nghĩ, phân tích và tìm tòi để khám phá thế giới toán học đầy thú vị!