Chào mừng các em học sinh lớp 8 đến với chuyên mục giải bài tập Toán 8 của giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 2 trang 3 và 4 sách giáo khoa Toán 8, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết cung cấp những phương pháp giải bài tập tối ưu, giúp các em hiểu sâu sắc bản chất của vấn đề.
Cho đơn thức
Cho ba ví dụ về đơn thức thu gọn và cho biết hệ số, phần biến và bậc của đơn thức thu gọn trong mỗi ví dụ.
Phương pháp giải:
Lấy ba ví dụ về đơn thức thu gọn.
Xác định hệ số, phần biến và bậc của từng đơn thức.
Lời giải chi tiết:
Ví dụ về đơn thức thu gọn:
- Đơn thức \(xy\) có: hệ số là 1; phần biến là \(xy\); bậc là 2
- Đơn thức \(\frac{{ - 1}}{2}{x^2}\) có: hệ số là \(\frac{{ - 1}}{2}\); phần biến là \({x^2}\) và bậc là 2.
- Đơn thức \(3{x^2}{y^4}\) có: hệ số là \(3\); phần biến là \({x^2}{y^4}\) và bậc là 6
Cho đơn thức \(3x{y^4}z{x^2}y{z^3}\)
a) Ta đã sử dụng các tính chất nào của phép nhân các số để suy ra
\(3x{y^4}z{x^2}y{z^3} = 3x{x^2}{y^4}yz{z^3}\)
b) Dựa vào quy tắc nhân hai lũy thừa cùng cơ số, hãy tìm các số mũ thích hợp cho các ô trong đẳng thức sau:
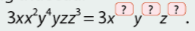
c) So sánh tổng số mũ của tất cả các biến có trong đơn thức \(3x{y^4}z{x^2}y{z^3}\) với tổng số cũ của tất cả các biến có trong đơn thức ở vế phải của đẳng thức trong câu b.
Phương pháp giải:
a) Nhắc lại các tính chất của phép nhân.
Quan sát trả lời câu hỏi.
b) Dựa và quy tắc nhân hai lũy thừa cùng cơ số: \({a^m}.{a^n} = {a^{m + n}}\)
Điền số mũ thích hợp
c) Tính tổng số mũ của tất cả các biến có trong đơn thức \(3x{y^4}z{x^2}y{z^3}\) và tổng số mũ của tất cả các biến có trong đơn thức ở vế phải của đẳng thức trong câu b. So sánh.
Lời giải chi tiết:
a) Ta đã sử dụng tính chất giao hoán của phép nhân các số để suy ra \(3x{y^4}z{x^2}y{z^3}\).
b) Điền các số mũ thích hợp trong đẳng thức, ta được:
\(3x{y^4}z{x^2}y{z^3} = 3{x^3}{y^5}{z^4}\)
c) Tổng số mũ của tất cả các biến có trong đơn thức \(3x{y^4}z{x^2}y{z^3}\) là: \(1 + 4 + 1 + 2 + 1 + 3 = 12\)
Tổng số mũ của tất cả các biến có trong đơn thức ở vế phải của đẳng thức trong câu b là \(3 + 5 + 4 = 12\)
Vậy tổng số mũ của tất cả các biến có trong đơn thức \(3x{y^4}z{x^2}y{z^3}\) bằng tổng số cũ của tất cả các biến có trong đơn thức ở vế phải của đẳng thức trong câu b.
Cho đơn thức \(3x{y^4}z{x^2}y{z^3}\)
a) Ta đã sử dụng các tính chất nào của phép nhân các số để suy ra
\(3x{y^4}z{x^2}y{z^3} = 3x{x^2}{y^4}yz{z^3}\)
b) Dựa vào quy tắc nhân hai lũy thừa cùng cơ số, hãy tìm các số mũ thích hợp cho các ô trong đẳng thức sau:
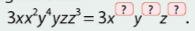
c) So sánh tổng số mũ của tất cả các biến có trong đơn thức \(3x{y^4}z{x^2}y{z^3}\) với tổng số cũ của tất cả các biến có trong đơn thức ở vế phải của đẳng thức trong câu b.
Phương pháp giải:
a) Nhắc lại các tính chất của phép nhân.
Quan sát trả lời câu hỏi.
b) Dựa và quy tắc nhân hai lũy thừa cùng cơ số: \({a^m}.{a^n} = {a^{m + n}}\)
Điền số mũ thích hợp
c) Tính tổng số mũ của tất cả các biến có trong đơn thức \(3x{y^4}z{x^2}y{z^3}\) và tổng số mũ của tất cả các biến có trong đơn thức ở vế phải của đẳng thức trong câu b. So sánh.
Lời giải chi tiết:
a) Ta đã sử dụng tính chất giao hoán của phép nhân các số để suy ra \(3x{y^4}z{x^2}y{z^3}\).
b) Điền các số mũ thích hợp trong đẳng thức, ta được:
\(3x{y^4}z{x^2}y{z^3} = 3{x^3}{y^5}{z^4}\)
c) Tổng số mũ của tất cả các biến có trong đơn thức \(3x{y^4}z{x^2}y{z^3}\) là: \(1 + 4 + 1 + 2 + 1 + 3 = 12\)
Tổng số mũ của tất cả các biến có trong đơn thức ở vế phải của đẳng thức trong câu b là \(3 + 5 + 4 = 12\)
Vậy tổng số mũ của tất cả các biến có trong đơn thức \(3x{y^4}z{x^2}y{z^3}\) bằng tổng số cũ của tất cả các biến có trong đơn thức ở vế phải của đẳng thức trong câu b.
Cho ba ví dụ về đơn thức thu gọn và cho biết hệ số, phần biến và bậc của đơn thức thu gọn trong mỗi ví dụ.
Phương pháp giải:
Lấy ba ví dụ về đơn thức thu gọn.
Xác định hệ số, phần biến và bậc của từng đơn thức.
Lời giải chi tiết:
Ví dụ về đơn thức thu gọn:
- Đơn thức \(xy\) có: hệ số là 1; phần biến là \(xy\); bậc là 2
- Đơn thức \(\frac{{ - 1}}{2}{x^2}\) có: hệ số là \(\frac{{ - 1}}{2}\); phần biến là \({x^2}\) và bậc là 2.
- Đơn thức \(3{x^2}{y^4}\) có: hệ số là \(3\); phần biến là \({x^2}{y^4}\) và bậc là 6
Mục 2 trong SGK Toán 8 trang 3 và 4 thường tập trung vào các kiến thức cơ bản về phép nhân đa thức, các hằng đẳng thức đáng nhớ và ứng dụng của chúng vào giải bài tập. Việc nắm vững các kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo của môn Toán.
Phép nhân đa thức là một trong những phép toán cơ bản trong đại số. Để nhân hai đa thức, ta áp dụng tính chất phân phối của phép nhân đối với phép cộng. Cụ thể, ta nhân mỗi hạng tử của đa thức thứ nhất với mỗi hạng tử của đa thức thứ hai, sau đó cộng các tích lại với nhau.
Ví dụ: (x + 2)(x - 3) = x(x - 3) + 2(x - 3) = x2 - 3x + 2x - 6 = x2 - x - 6
Các hằng đẳng thức đáng nhớ là những biểu thức đại số luôn đúng với mọi giá trị của biến. Việc nắm vững các hằng đẳng thức này giúp ta giải bài tập nhanh chóng và hiệu quả hơn.
Bài 1: Thực hiện phép tính: (2x + 1)(x - 5)
Lời giải: (2x + 1)(x - 5) = 2x(x - 5) + 1(x - 5) = 2x2 - 10x + x - 5 = 2x2 - 9x - 5
Bài 2: Rút gọn biểu thức: (x + 3)2 - (x - 3)2
Lời giải: (x + 3)2 - (x - 3)2 = (x2 + 6x + 9) - (x2 - 6x + 9) = x2 + 6x + 9 - x2 + 6x - 9 = 12x
Để giải bài tập Toán 8 một cách hiệu quả, các em cần:
Phép nhân đa thức và các hằng đẳng thức không chỉ có ý nghĩa trong môn Toán mà còn được ứng dụng rộng rãi trong các lĩnh vực khác của đời sống, như vật lý, hóa học, kinh tế,... Ví dụ, trong vật lý, ta có thể sử dụng các hằng đẳng thức để tính toán vận tốc, gia tốc, năng lượng,...
Để học tốt môn Toán 8, các em nên:
Hy vọng với những kiến thức và phương pháp giải bài tập được trình bày trên đây, các em sẽ tự tin hơn trong việc học môn Toán 8. Chúc các em học tốt!