Chào mừng các em học sinh đến với bài giải chi tiết mục 2 trang 61, 62 sách giáo khoa Toán 8. Tại giaitoan.edu.vn, chúng tôi cung cấp các lời giải bài tập Toán 8 được trình bày rõ ràng, dễ hiểu, giúp các em tự tin hơn trong việc học tập.
Mục tiêu của chúng tôi là hỗ trợ các em học sinh nắm vững kiến thức Toán học, rèn luyện kỹ năng giải bài tập và đạt kết quả tốt nhất trong các kỳ thi.
1. Vẽ hai tứ giác bất kì. Đo và tính tổng các góc của mỗi tứ giác
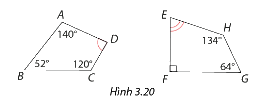
Tính số đo góc D và góc E của các tứ giác trong Hình 3.20.
Phương pháp giải:
Tổng các góc của một tứ giác bằng \(360^\circ \). Từ đó tìm được góc D và E.
Lời giải chi tiết:
Ta có số đo góc D là: \(\widehat D = 360^\circ - \left( {\widehat A + \widehat B + \widehat C} \right) = 360^\circ - \left( {140^\circ + 52^\circ + 120^\circ } \right) = 48^\circ \)
Số đo góc E là: \(\widehat E = 360^\circ - \left( {\widehat H + \widehat G + \widehat F} \right) = 360^\circ - \left( {134^\circ + 64^\circ + 90^\circ } \right) = 72^\circ \).
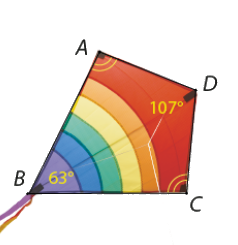
Cánh diều hình tứ giác \(ABCD\) có \(\widehat D = 107^\circ ,\widehat B = 63^\circ \) và \(\widehat A = \widehat C\) (Hình 3.21). Tính số đo góc A và góc C của cánh diều.
Phương pháp giải:
Tổng các góc của một tứ giác bằng \(360^\circ \). Từ đó tìm được góc A và C.
Lời giải chi tiết:
Gọi số đo góc \(\widehat A\) là \(x\) thì \(\widehat A = \widehat C = x\)
Ta có:
\(\begin{array}{l}360^\circ = \widehat A + \widehat B + \widehat C + \widehat D = x + x + 107 + 63 = 2x + 170\\ = > x = \left( {360^\circ - 170^\circ } \right):2 = 190^\circ :2 = 95^\circ \end{array}\)
Vậy \(\widehat A = \widehat C = 95^\circ \).
Phương pháp giải:
Vẽ hai tứ giác bất kì sau đó đo và tính tổng các góc của mỗi tứ giác. Nhận xét về hai tổng.
So sánh tổng các góc của tứ giác \(ABCD\) với tổng các góc của hai tam giác \(ABD\) và \(BCD\), từ đó tính tổng các góc của tứ giác \(ABCD\)
Lời giải chi tiết:
a)
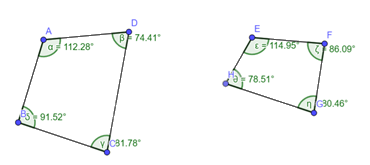
Nhận xét: Tổng của cả hai tứ giác đều bằng \(360^\circ \).
b) Ta có:
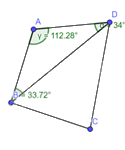
Tổng các góc của tam giác \(ABD\) là \(112,28 + 34 + 33,72 = 180^\circ \)
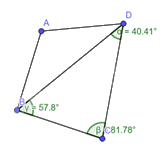
Tổng các góc của tam giác \(BCD\) là: \(40,41 + 81,78 + 57,8 = 180^\circ \)
Vậy tổng của tứ giác \(ABCD\) là \(180^\circ + 180^\circ = 360^\circ \).
Phương pháp giải:
Vẽ hai tứ giác bất kì sau đó đo và tính tổng các góc của mỗi tứ giác. Nhận xét về hai tổng.
So sánh tổng các góc của tứ giác \(ABCD\) với tổng các góc của hai tam giác \(ABD\) và \(BCD\), từ đó tính tổng các góc của tứ giác \(ABCD\)
Lời giải chi tiết:
a)
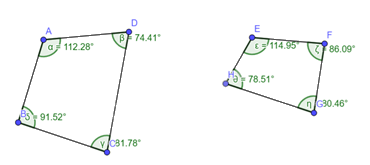
Nhận xét: Tổng của cả hai tứ giác đều bằng \(360^\circ \).
b) Ta có:
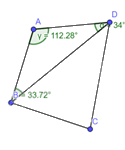
Tổng các góc của tam giác \(ABD\) là \(112,28 + 34 + 33,72 = 180^\circ \)
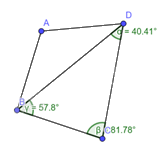
Tổng các góc của tam giác \(BCD\) là: \(40,41 + 81,78 + 57,8 = 180^\circ \)
Vậy tổng của tứ giác \(ABCD\) là \(180^\circ + 180^\circ = 360^\circ \).
Tính số đo góc D và góc E của các tứ giác trong Hình 3.20.
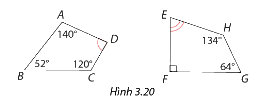
Phương pháp giải:
Tổng các góc của một tứ giác bằng \(360^\circ \). Từ đó tìm được góc D và E.
Lời giải chi tiết:
Ta có số đo góc D là: \(\widehat D = 360^\circ - \left( {\widehat A + \widehat B + \widehat C} \right) = 360^\circ - \left( {140^\circ + 52^\circ + 120^\circ } \right) = 48^\circ \)
Số đo góc E là: \(\widehat E = 360^\circ - \left( {\widehat H + \widehat G + \widehat F} \right) = 360^\circ - \left( {134^\circ + 64^\circ + 90^\circ } \right) = 72^\circ \).
Cánh diều hình tứ giác \(ABCD\) có \(\widehat D = 107^\circ ,\widehat B = 63^\circ \) và \(\widehat A = \widehat C\) (Hình 3.21). Tính số đo góc A và góc C của cánh diều.
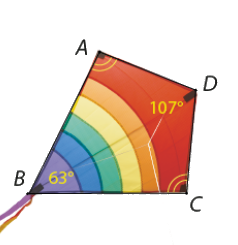
Phương pháp giải:
Tổng các góc của một tứ giác bằng \(360^\circ \). Từ đó tìm được góc A và C.
Lời giải chi tiết:
Gọi số đo góc \(\widehat A\) là \(x\) thì \(\widehat A = \widehat C = x\)
Ta có:
\(\begin{array}{l}360^\circ = \widehat A + \widehat B + \widehat C + \widehat D = x + x + 107 + 63 = 2x + 170\\ = > x = \left( {360^\circ - 170^\circ } \right):2 = 190^\circ :2 = 95^\circ \end{array}\)
Vậy \(\widehat A = \widehat C = 95^\circ \).
Mục 2 của chương trình Toán 8 thường tập trung vào các kiến thức về hình học, cụ thể là các loại tứ giác đặc biệt như hình bình hành, hình chữ nhật, hình thoi, hình vuông. Việc nắm vững các tính chất, dấu hiệu nhận biết và các ứng dụng của các tứ giác này là vô cùng quan trọng để giải quyết các bài tập liên quan.
Mục 2 thường bao gồm các nội dung sau:
Để giải tốt các bài tập trong Mục 2, các em cần:
Bài tập: Cho hình bình hành ABCD. Gọi E là trung điểm của cạnh AB. Gọi F là giao điểm của DE và AC. Chứng minh rằng AF = FC.
Giải:
Để củng cố kiến thức và kỹ năng giải bài tập, các em nên luyện tập thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Ngoài ra, các em có thể tham khảo các bài giảng trực tuyến và các video hướng dẫn giải bài tập trên giaitoan.edu.vn.
Học Toán đòi hỏi sự kiên trì và luyện tập thường xuyên. Hãy dành thời gian ôn tập lý thuyết, làm bài tập và tìm hiểu các phương pháp giải bài tập khác nhau. Đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè khi gặp khó khăn. Chúc các em học tốt môn Toán!
| Tứ giác | Tính chất |
|---|---|
| Hình bình hành | Các cạnh đối song song và bằng nhau, các góc đối bằng nhau, hai đường chéo cắt nhau tại trung điểm của mỗi đường. |
| Hình chữ nhật | Có bốn góc vuông, hai đường chéo bằng nhau. |
| Hình thoi | Có bốn cạnh bằng nhau, hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường. |
| Hình vuông | Vừa là hình chữ nhật, vừa là hình thoi. |