Chào mừng bạn đến với bài học về Lý thuyết Tứ giác SGK Toán 8 trên giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về tứ giác, giúp bạn hiểu rõ các khái niệm, tính chất và ứng dụng của nó trong giải toán.
Chúng tôi cam kết mang đến cho bạn một trải nghiệm học tập hiệu quả và thú vị với phương pháp trình bày dễ hiểu, bài tập thực hành đa dạng và đội ngũ giáo viên giàu kinh nghiệm.
Tứ giác lồi là gì?
1. Tứ giác lồi
Tứ giác lồi là tứ giác mà hai đỉnh thuộc một cạnh bất kì luôn nằm về một phía của đường thẳng đi qua hai đỉnh còn lại.
Ví dụ:
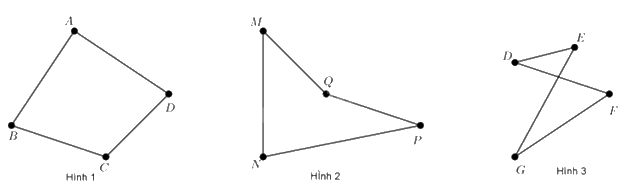
Hình 1 là tứ giác lồi.
2. Tổng các góc của một tứ giác
Tổng các góc của một tứ giác bằng \({360^0}\)
Ví dụ:
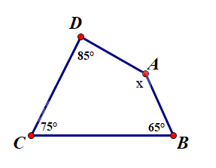
Theo định lí về tổng các góc của một tứ giác, ta có \(\widehat A + \widehat B + \widehat C + \widehat D = {360^0}\). Do đó \(\widehat A = x = {360^0} - {85^0} - {75^0} - {65^0} = {135^0}\)
Vậy \(\widehat A = {135^0}\)

Tứ giác là một trong những khái niệm cơ bản và quan trọng trong hình học lớp 8. Việc nắm vững lý thuyết về tứ giác không chỉ giúp học sinh giải quyết các bài toán trong sách giáo khoa mà còn là nền tảng cho việc học các kiến thức hình học nâng cao hơn.
Tứ giác là hình có bốn cạnh và bốn góc. Bốn đỉnh của tứ giác là bốn điểm bất kỳ trên mặt phẳng, không có ba điểm nào thẳng hàng. Tứ giác được ký hiệu là ABCD, với A, B, C, D là các đỉnh của tứ giác.
Có một số loại tứ giác đặc biệt thường gặp trong chương trình Toán 8:
Tổng bốn góc của một tứ giác bằng 360 độ. Đây là một tính chất quan trọng và thường được sử dụng để giải các bài toán liên quan đến tứ giác.
Có một số dấu hiệu để nhận biết các loại tứ giác đặc biệt:
Để củng cố kiến thức về tứ giác, bạn có thể thực hành giải các bài tập sau:
Lý thuyết tứ giác có nhiều ứng dụng trong thực tế, ví dụ như:
Hy vọng bài học về Lý thuyết Tứ giác SGK Toán 8 này sẽ giúp bạn hiểu rõ hơn về khái niệm và ứng dụng của tứ giác trong môn Toán. Chúc bạn học tập tốt!