Định lí Pythagore là một trong những định lý quan trọng nhất trong hình học, được học trong chương trình Toán 8. Nó mô tả mối quan hệ giữa các cạnh của một tam giác vuông và có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp tài liệu học tập đầy đủ và dễ hiểu về Định lí Pythagore, giúp bạn nắm vững kiến thức và tự tin giải các bài tập.
Định lí Pythagore
1. Định lí Pythagore
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
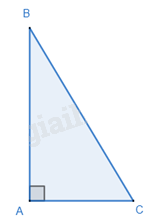
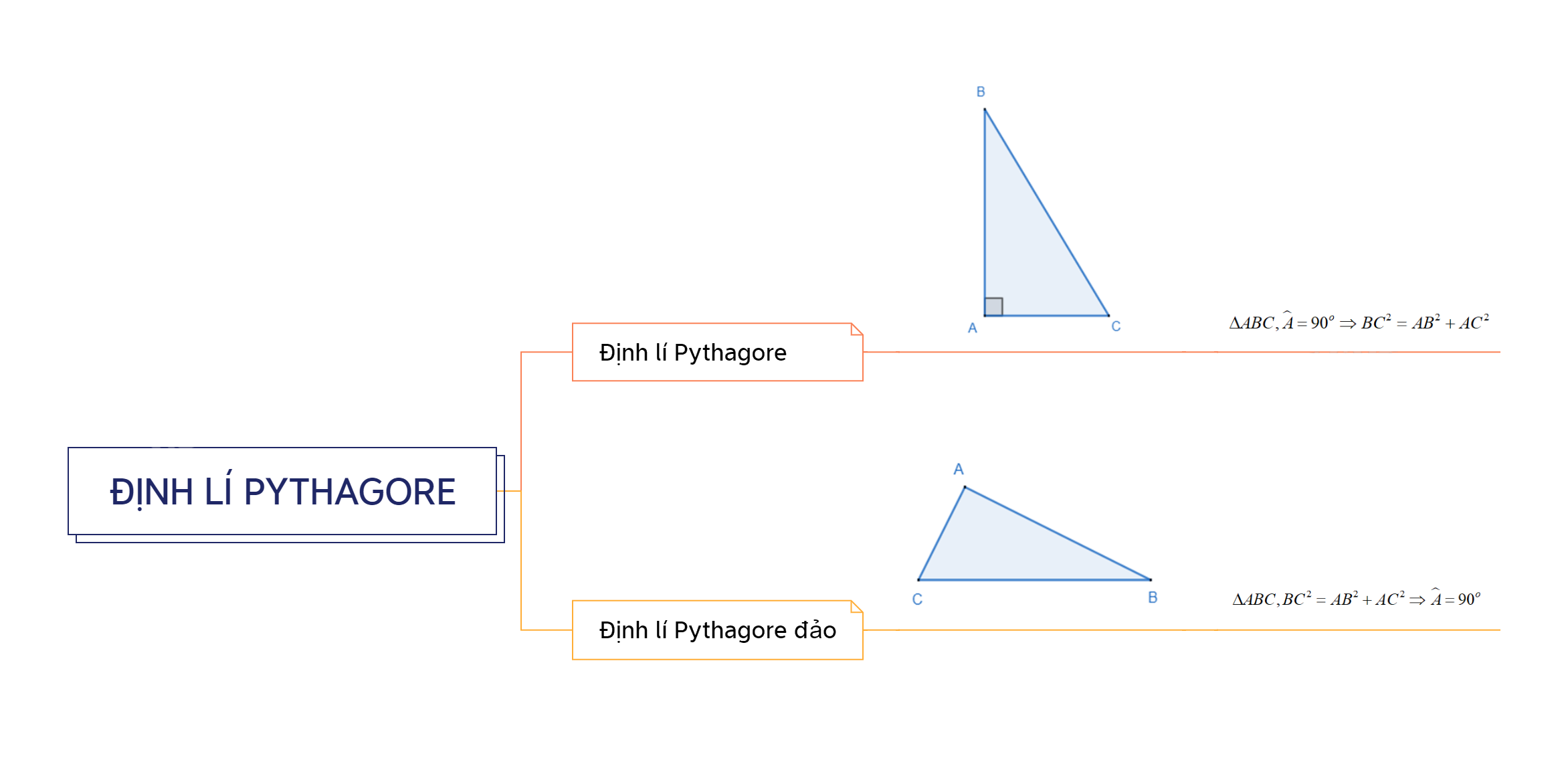
\(\Delta ABC,\widehat A = {90^o} \Rightarrow B{C^2} = A{B^2} + A{C^2}\)
2. Định lí Pythagore đảo
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương độ dài của hai cạnh kia thì tam giác đó là tam giác vuông.
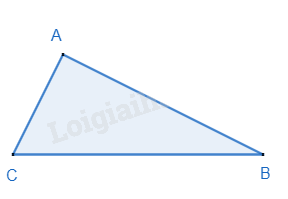
\(\Delta ABC,B{C^2} = A{B^2} + A{C^2} \Rightarrow \widehat A = {90^o}\)
Ví dụ:
Tam giác ABC có AB = 3cm, BC = 5cm, AC = 4cm thì tam giác ABC vuông tại A do \({3^2} + {4^2} = {5^2}\), suy ra \(B{C^2} = A{B^2} + A{C^2}\).
Định lí Pythagore phát biểu rằng: Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông. Công thức toán học của định lý này là: a2 + b2 = c2, trong đó 'c' là độ dài cạnh huyền và 'a', 'b' là độ dài hai cạnh góc vuông.
Trước khi đi sâu vào định lý, chúng ta cần hiểu rõ khái niệm tam giác vuông. Tam giác vuông là tam giác có một góc bằng 90 độ. Cạnh đối diện với góc vuông được gọi là cạnh huyền, và hai cạnh còn lại được gọi là các cạnh góc vuông.
Có nhiều cách để chứng minh Định lí Pythagore. Một trong những cách phổ biến nhất là sử dụng diện tích. Chúng ta có thể sắp xếp các hình vuông xây dựng trên các cạnh của tam giác vuông để chứng minh mối quan hệ a2 + b2 = c2.
(Hình minh họa chứng minh Định lí Pythagore bằng diện tích có thể được chèn vào đây)
Ví dụ 1: Cho tam giác ABC vuông tại A, AB = 3cm, AC = 4cm. Tính độ dài cạnh BC.
Giải: Áp dụng Định lí Pythagore, ta có: BC2 = AB2 + AC2 = 32 + 42 = 9 + 16 = 25. Vậy BC = √25 = 5cm.
Ví dụ 2: Cho tam giác DEF có DE = 5cm, EF = 12cm, DF = 13cm. Chứng minh tam giác DEF là tam giác vuông.
Giải: Ta có: DE2 + EF2 = 52 + 122 = 25 + 144 = 169. Và DF2 = 132 = 169. Vì DE2 + EF2 = DF2, nên tam giác DEF là tam giác vuông theo Định lí Pythagore.
Các bài tập về Định lí Pythagore thường gặp các dạng sau:
Định lí Pythagore có nhiều mở rộng và ứng dụng trong các lĩnh vực toán học cao hơn như hình học không gian, lượng giác, và giải tích. Việc nắm vững kiến thức cơ bản về Định lí Pythagore là nền tảng quan trọng để học tập các kiến thức nâng cao.
Để củng cố kiến thức về Định lí Pythagore, bạn nên luyện tập thêm nhiều bài tập khác nhau. giaitoan.edu.vn cung cấp một hệ thống bài tập đa dạng và phong phú, giúp bạn rèn luyện kỹ năng giải toán và tự tin hơn trong các kỳ thi.
Hãy truy cập giaitoan.edu.vn để khám phá thêm nhiều kiến thức và bài tập về Định lí Pythagore và các chủ đề Toán 8 khác!