Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8. Chúng tôi hiểu rằng việc giải các bài tập trong SGK Toán 8 có thể gặp nhiều khó khăn, đặc biệt là với những em học sinh mới làm quen với chương trình.
Với mục tiêu giúp các em học sinh nắm vững kiến thức và tự tin hơn trong học tập, chúng tôi đã biên soạn bộ giải đáp đầy đủ cho từng trang sách, bắt đầu từ Giải câu hỏi trang 4 SGK Toán 8.
Bàn cờ vua có 8 cột
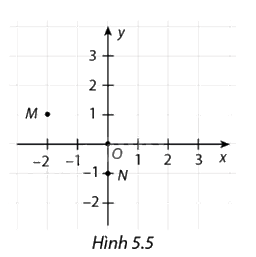
Cho Hình 5.5.
a) Xác định tọa độ các điểm \(O,M,N\).
b) Xác định tọa độ điểm \(P\) tùy ý thuộc \(Ox\), tọa độ điểm \(Q\) tùy ý thuộc \(Oy\).
Phương pháp giải:
Trong mặt phẳng tọa độ \(Oxy\), mỗi điểm M được xác định bởi cặp số \(\left( {{x_0};{y_0}} \right)\) và ngược lại
Cặp số \(\left( {{x_0};{y_0}} \right)\) được gọi là tọa độ của điểm M. Số \({x_0}\) gọi là hoành độ và số \({y_0}\) gọi là tung độ của điểm M. Nếu \(\left( {{x_0};{y_0}} \right)\) là tọa độ của điểm M thì ta viết là \(M\left( {{x_0};{y_0}} \right)\).
Lời giải chi tiết:
a) Quan sát Hình 5.5. Xét điểm O ta thấy các đường thẳng vuông góc kẻ từ điểm O xuống trục hoành và trục tung bằng chính điểm O vậy ta có tọa độ \(O\left( {0;0} \right)\). Tương tự với điểm M có tọa độ là \(M\left( { - 2;1} \right)\) và điểm N có tọa độ là \(N\left( {0; - 1} \right)\).
b) Tọa độ điểm P tùy ý thuộc \(Ox\) thì sẽ có hoành độ bằng 0: \(P\left( {2;0} \right)\)
Tọa độ điểm Q tùy ý thuộc \(Oy\) thì sẽ có tung độ bằng 0: \(Q\left( { - 2;0} \right)\)
Vẽ một hệ trục tọa độ \(Oxy\) và đánh dấu vị trí của các điểm \(P\left( {1;3} \right),Q\left( {3;1} \right),R\left( { - 2;2} \right)\)
Mỗi điểm này thuộc góc phần tư nào của mặt phẳng tọa độ?
Phương pháp giải:
Dựa vào cách vẽ mặt phẳng tọa độ và cách xác định vị trí tọa độ các điểm để vẽ được hệ trục tọa độ \(Oxy\) và đánh dấu vị trí của các điểm.
Lời giải chi tiết:
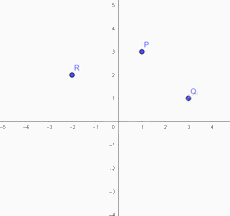
Điểm P thuộc góc phần tư thứ I của mặt phẳng tọa độ
Điểm Q thuộc góc phần tư thứ I của mặt phẳng tọa độ
Điểm R thuộc góc phần tư thứ II của mặt phẳng tọa độ
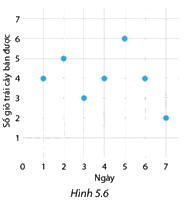
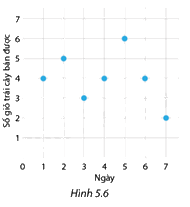
Hình 5.6 biểu diễn số giỏ trái cây bán được trong tuần đầu khai trương của một cửa hàng.
a) Trong ngày đầu khai trường, cửa hàng bán được bao nhiêu giỏ trái cây?
b) Cửa hàng bán được nhiều giỏ trái cây nhất vào ngày thứ mấy trong tuần đầu khai trương và bán được bao nhiêu giỏ?
Phương pháp giải:
Dựa vào cách xác định vị trí tọa độ điểm trong mặt phẳng tọa độ để xác định cửa hàng bán được bao nhiêu giỏ trái cây trong ngày đầu khai trương và bán được nhiều nhất vào ngày thứ mấy.
Lời giải chi tiết:
a) Trong ngày đầu khai trương, cửa hàng bán được 4 giỏ trái cây
b) Cửa hàng bán được nhiều giỏ trái cây nhất vào ngày thứ 5 bán được 6 giỏ trái cây.
Bàn cờ vua có 8 cột \(\left( {a,b,c,d,e,f,g,h} \right)\) và 8 hàng \(\left( {1,2,3,4,5,6,7,8} \right)\). Trong Hình 5.1, trên bàn cờ của ván đang chơi còn một quân mã.
a) Xác định vị trí của quân mã trên bàn cờ. Giải thích cách xác định vị trí đó.
b) Xác định các vị trí quân mã này có thể di chuyển đến sau một nước đi từ ô đang đứng, biết rằng theo quy tắc chơi, quân mã được di theo đường chéo của hình chữ nhật có kích thước \(2 \times 3\) ô.

Phương pháp giải:
Ta dùng hai yếu tố hàng ngang và cột dọc để xác định vị trí của quân mã và xác định các vị trí quân mã này có thể di chuyển đến sau một nước đi từ ô đang đứng.
Lời giải chi tiết:
a) Vị trí của quân mã trên bàn cờ: hàng số 8 cột b
b) Các vị trí quân mã có thể di chuyển đến sau một nước đi từ ô đang đứng:
Hàng 6 cột a
Hàng 6 cột c
Hàng 7 cột d
Bàn cờ vua có 8 cột \(\left( {a,b,c,d,e,f,g,h} \right)\) và 8 hàng \(\left( {1,2,3,4,5,6,7,8} \right)\). Trong Hình 5.1, trên bàn cờ của ván đang chơi còn một quân mã.
a) Xác định vị trí của quân mã trên bàn cờ. Giải thích cách xác định vị trí đó.
b) Xác định các vị trí quân mã này có thể di chuyển đến sau một nước đi từ ô đang đứng, biết rằng theo quy tắc chơi, quân mã được di theo đường chéo của hình chữ nhật có kích thước \(2 \times 3\) ô.

Phương pháp giải:
Ta dùng hai yếu tố hàng ngang và cột dọc để xác định vị trí của quân mã và xác định các vị trí quân mã này có thể di chuyển đến sau một nước đi từ ô đang đứng.
Lời giải chi tiết:
a) Vị trí của quân mã trên bàn cờ: hàng số 8 cột b
b) Các vị trí quân mã có thể di chuyển đến sau một nước đi từ ô đang đứng:
Hàng 6 cột a
Hàng 6 cột c
Hàng 7 cột d
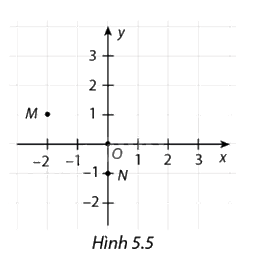
Cho Hình 5.5.
a) Xác định tọa độ các điểm \(O,M,N\).
b) Xác định tọa độ điểm \(P\) tùy ý thuộc \(Ox\), tọa độ điểm \(Q\) tùy ý thuộc \(Oy\).
Phương pháp giải:
Trong mặt phẳng tọa độ \(Oxy\), mỗi điểm M được xác định bởi cặp số \(\left( {{x_0};{y_0}} \right)\) và ngược lại
Cặp số \(\left( {{x_0};{y_0}} \right)\) được gọi là tọa độ của điểm M. Số \({x_0}\) gọi là hoành độ và số \({y_0}\) gọi là tung độ của điểm M. Nếu \(\left( {{x_0};{y_0}} \right)\) là tọa độ của điểm M thì ta viết là \(M\left( {{x_0};{y_0}} \right)\).
Lời giải chi tiết:
a) Quan sát Hình 5.5. Xét điểm O ta thấy các đường thẳng vuông góc kẻ từ điểm O xuống trục hoành và trục tung bằng chính điểm O vậy ta có tọa độ \(O\left( {0;0} \right)\). Tương tự với điểm M có tọa độ là \(M\left( { - 2;1} \right)\) và điểm N có tọa độ là \(N\left( {0; - 1} \right)\).
b) Tọa độ điểm P tùy ý thuộc \(Ox\) thì sẽ có hoành độ bằng 0: \(P\left( {2;0} \right)\)
Tọa độ điểm Q tùy ý thuộc \(Oy\) thì sẽ có tung độ bằng 0: \(Q\left( { - 2;0} \right)\)
Vẽ một hệ trục tọa độ \(Oxy\) và đánh dấu vị trí của các điểm \(P\left( {1;3} \right),Q\left( {3;1} \right),R\left( { - 2;2} \right)\)
Mỗi điểm này thuộc góc phần tư nào của mặt phẳng tọa độ?
Phương pháp giải:
Dựa vào cách vẽ mặt phẳng tọa độ và cách xác định vị trí tọa độ các điểm để vẽ được hệ trục tọa độ \(Oxy\) và đánh dấu vị trí của các điểm.
Lời giải chi tiết:
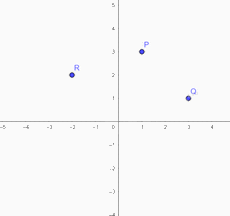
Điểm P thuộc góc phần tư thứ I của mặt phẳng tọa độ
Điểm Q thuộc góc phần tư thứ I của mặt phẳng tọa độ
Điểm R thuộc góc phần tư thứ II của mặt phẳng tọa độ
Hình 5.6 biểu diễn số giỏ trái cây bán được trong tuần đầu khai trương của một cửa hàng.
a) Trong ngày đầu khai trường, cửa hàng bán được bao nhiêu giỏ trái cây?
b) Cửa hàng bán được nhiều giỏ trái cây nhất vào ngày thứ mấy trong tuần đầu khai trương và bán được bao nhiêu giỏ?
Phương pháp giải:
Dựa vào cách xác định vị trí tọa độ điểm trong mặt phẳng tọa độ để xác định cửa hàng bán được bao nhiêu giỏ trái cây trong ngày đầu khai trương và bán được nhiều nhất vào ngày thứ mấy.
Lời giải chi tiết:
a) Trong ngày đầu khai trương, cửa hàng bán được 4 giỏ trái cây
b) Cửa hàng bán được nhiều giỏ trái cây nhất vào ngày thứ 5 bán được 6 giỏ trái cây.
Trang 4 SGK Toán 8 thường chứa các bài tập về các phép toán cơ bản, các tính chất của số tự nhiên, số nguyên, phân số và các biểu thức đại số đơn giản. Việc nắm vững kiến thức nền tảng này là vô cùng quan trọng để học tốt các chương tiếp theo của môn Toán 8.
Thông thường, trang 4 SGK Toán 8 sẽ bao gồm các dạng bài tập sau:
Để giải tốt các bài tập trang 4 SGK Toán 8, các em cần nắm vững các kiến thức sau:
Bài tập 1: Tính 12 + 5 x 2
Giải:
Áp dụng thứ tự thực hiện các phép toán, ta thực hiện phép nhân trước:
5 x 2 = 10
Sau đó thực hiện phép cộng:
12 + 10 = 22
Vậy, 12 + 5 x 2 = 22
Giaitoan.edu.vn cung cấp:
Ngoài giải bài tập trang 4 SGK Toán 8, giaitoan.edu.vn còn cung cấp các tài liệu học Toán 8 hữu ích khác như:
Hy vọng rằng với những thông tin và lời giải chi tiết trên đây, các em học sinh sẽ tự tin hơn trong việc giải các bài tập trang 4 SGK Toán 8 và học tốt môn Toán 8. Hãy truy cập giaitoan.edu.vn để khám phá thêm nhiều tài liệu học Toán 8 hữu ích khác nhé!