Chào mừng bạn đến với bài học về Lý thuyết Hàm số và đồ thị của hàm số trong chương trình SGK Toán 8 tại giaitoan.edu.vn. Đây là một trong những chủ đề quan trọng, đặt nền móng cho các kiến thức toán học nâng cao hơn.
Chúng tôi cung cấp lý thuyết đầy đủ, dễ hiểu cùng với các ví dụ minh họa chi tiết, giúp bạn nắm vững khái niệm và ứng dụng của hàm số và đồ thị hàm số.
Hàm số là gì?
1. Hàm số
Định nghĩa:
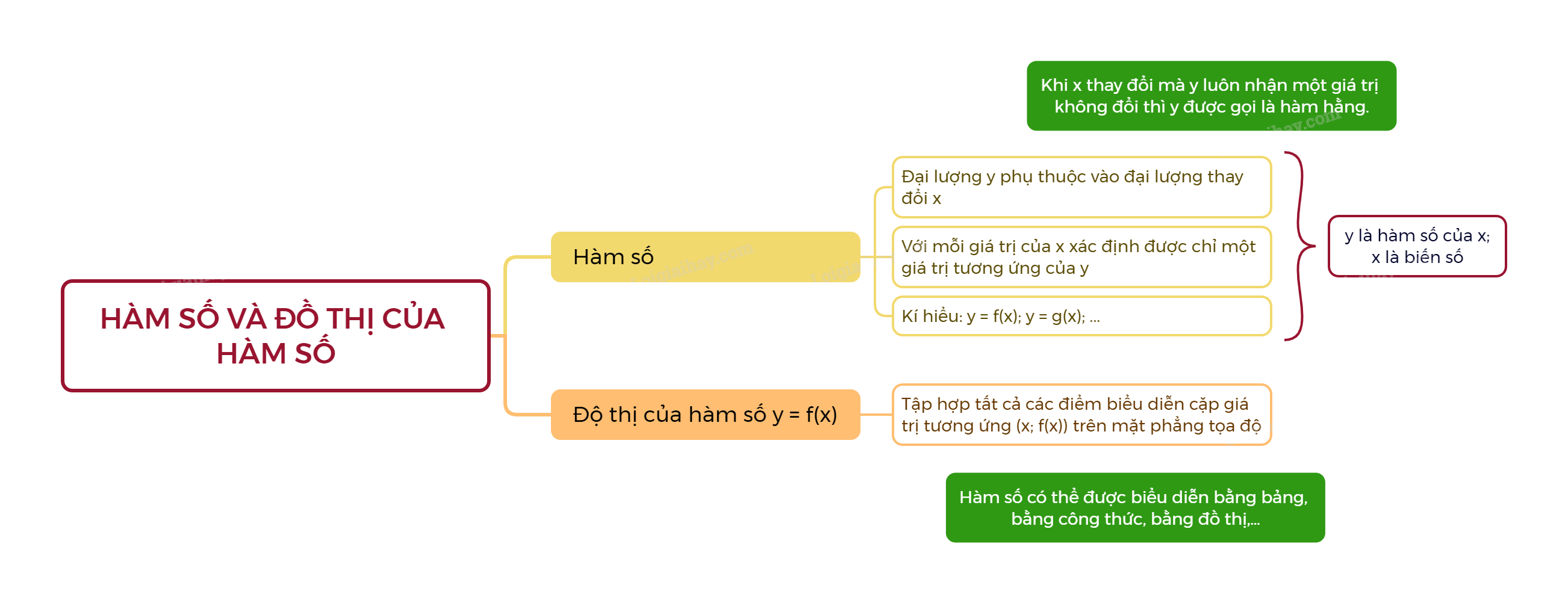
Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x gọi là biến số.
Ví dụ: Ta có bảng nhiệt độ dự báo ở Thủ đô Hà Nội ngày 25/5/2023.
t(h) | 10 | 11 | 12 | 13 |
T(0C) | 32 | 33 | 34 | 34 |
Ta có nhiệt độ T là hàm số của thời điểm t vì mỗi giá trị của t chỉ xác định đúng một giá trị của T.
Ngược lại, thời điểm t không phải là hàm số của nhiệt độ T, vì nhiệt độ T = 340C tương ứng với hai thời điểm khác nhau t = 12 và t = 13.
Lưu ý:
- Khi x thay đổi mà y luôn nhận một giá trị không đổi thì y được gọi là hàm hằng.
- Khi y là hàm số của x, ta có thể viết y = f(x), y = g(x),…
Ví dụ: y= 2x – 3, ta có thể viết y = f(x) = 2x – 3
Khi x bằng 5, giá trị tương ứng của y = 7 , ta viết f(5) = 7.
2. Đồ thị của hàm số
Đồ thị của hàm số y = f(x) trên mặt phẳng tọa độ là tập hợp tất cả các điểm biểu diễn cặp giá trị tương ứng (x; f(x)) trên mặt phẳng đó.
Hàm số là một khái niệm cơ bản trong toán học, mô tả mối quan hệ giữa hai đại lượng. Trong chương trình Toán 8, học sinh bắt đầu làm quen với các loại hàm số đơn giản và cách biểu diễn chúng bằng đồ thị.
Một hàm số f được định nghĩa trên tập hợp A là một quy tắc tương ứng mỗi phần tử x thuộc A với duy nhất một phần tử y.
Đồ thị của hàm số y = f(x) là tập hợp tất cả các điểm trên mặt phẳng tọa độ có tọa độ (x; f(x)) với mọi x thuộc tập xác định của hàm số.
| Hệ số a | Tính chất của đồ thị |
|---|---|
| a > 0 | Đồ thị là đường thẳng đi lên từ trái sang phải. |
| a < 0 | Đồ thị là đường thẳng đi xuống từ trái sang phải. |
Hàm số và đồ thị hàm số có nhiều ứng dụng trong thực tế, ví dụ như:
Bài 1: Vẽ đồ thị hàm số y = 2x - 1.
Giải:
Bài 2: Xác định hệ số a của hàm số y = ax + 2 biết rằng đồ thị của hàm số đi qua điểm M(1; 5).
Giải:
Thay tọa độ điểm M(1; 5) vào phương trình hàm số, ta có: 5 = a * 1 + 2 => a = 3.
Để nắm vững kiến thức về hàm số và đồ thị hàm số, bạn nên luyện tập thêm nhiều bài tập khác nhau. giaitoan.edu.vn cung cấp một hệ thống bài tập phong phú, đa dạng với các mức độ khó khác nhau, giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải toán.
Chúc bạn học tốt!