Bài 5.34 trang 30 SGK Toán 8 là một bài tập quan trọng trong chương trình học Toán lớp 8. Bài tập này yêu cầu học sinh vận dụng kiến thức về hình học, cụ thể là các tính chất của hình thang cân để giải quyết vấn đề.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững phương pháp giải và tự tin làm bài tập.
Toàn và Thắng chơi một trò chơi như sau: Trên lưới ô vuông ghi các số tự nhiên từ 1 đến 100 như Hình 5.35,
Đề bài
Toàn và Thắng chơi một trò chơi như sau:
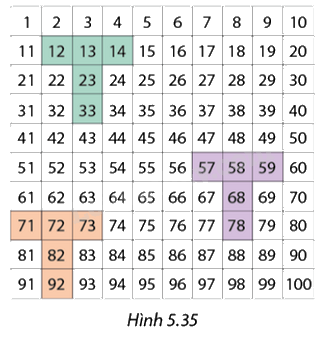
Trên lưới ô vuông ghi các số tự nhiên từ 1 đến 100 như Hình 5.35, Toàn tô màu một chữ T đi qua năm số và cho Thắng biết tổng của năm số đó. Nhiệm vụ của Thắng là chỉ ra vị trí của chữ T đã tô màu.
Trong một lượt chơi, Toàn thông báo tổng của năm số là 95. Sau vài bước tính toán, Thằng chỉ ra được vị trí của chữ T chính là 5 ô đã tô màu xanh trên lưới. Hãy giải thích cách làm của Thắng.
Phương pháp giải - Xem chi tiết
Vận dụng phương trình bậc nhất một ẩn để giải quyết nhiều vấn đề thực tiễn theo các bước sau:
Bước 1: Lập phương trình
- Chọn ẩn số và đặt điều kiện cho ẩn số
- Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết
- Lập phương trình biểu thị mối quan hệ giữa các đại lượng
Bước 2: Giải phương trình
Bước 3: Kiểm tra xem nghiệm có thỏa mãn điều kiện của ẩn hay không rồi kết luận.
Lời giải chi tiết
Gọi số đầu tiên bên trái dòng 1 của chữ T là x (x>0)
Thì số tiếp theo dòng 1 sẽ là \(x + 1\)
Số tiếp theo dòng 1 là \(x + 2\)
Số ở dòng thứ hai là \(x + 11\)
Số ở dòng thứ ba là \(x + 21\)
Toàn thông báo tổng của năm số là 95, ta có phương trình:
\(\begin{array}{l}x + \left( {x + 1} \right) + \left( {x + 2} \right) + \left( {x + 11} \right) + \left( {x + 21} \right) = 95\\5x + 35 = 95\\5x = 60\\x = 12\end{array}\)
Vậy số đầu tiên là 12, tiếp theo là 13, 14, 23 và 33.
Bài 5.34 trang 30 SGK Toán 8 thuộc chương trình Toán lớp 8, tập trung vào việc vận dụng các kiến thức về hình thang cân để giải quyết các bài toán thực tế. Để hiểu rõ hơn về cách giải bài tập này, chúng ta cùng đi vào phân tích chi tiết:
Đề bài thường yêu cầu chứng minh một tính chất liên quan đến hình thang cân, hoặc tính toán các yếu tố như độ dài đường trung bình, chiều cao, diện tích của hình thang cân. Ví dụ, một dạng bài tập phổ biến là:
Cho hình thang cân ABCD (AB // CD), có AD = BC. Chứng minh rằng AC = BD.
Để giải bài toán này, chúng ta cần nắm vững các kiến thức sau:
Hướng giải thường là chứng minh hai tam giác có chứa hai cạnh bên của hình thang cân bằng nhau theo trường hợp cạnh - góc - cạnh (c-g-c) hoặc cạnh - cạnh - cạnh (c-c-c).
Chứng minh:
Xét hai tam giác ADC và BCD, ta có:
Vậy, ΔADC = ΔBCD (c-g-c). Suy ra AC = BD (hai cạnh tương ứng).
Ngoài dạng bài chứng minh hai đường chéo bằng nhau, bài 5.34 trang 30 SGK Toán 8 còn có thể xuất hiện các dạng bài tập khác như:
Để giải các dạng bài tập này, chúng ta cần:
Để củng cố kiến thức về hình thang cân và rèn luyện kỹ năng giải bài tập, các em học sinh có thể tham khảo thêm các bài tập sau:
Khi giải bài tập về hình thang cân, các em cần lưu ý:
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn khi giải bài 5.34 trang 30 SGK Toán 8 và các bài tập tương tự. Chúc các em học tốt!