Chào mừng bạn đến với bài học về Lý thuyết Hình bình hành trong chương trình SGK Toán 8 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp cho bạn một cách hệ thống và dễ hiểu nhất về các khái niệm, tính chất và dấu hiệu nhận biết của hình bình hành.
Chúng tôi tin rằng, với sự hướng dẫn chi tiết và các ví dụ minh họa sinh động, bạn sẽ nắm vững kiến thức này và tự tin giải quyết các bài tập liên quan.
Hình bình hành là gì?
1. Khái niệm
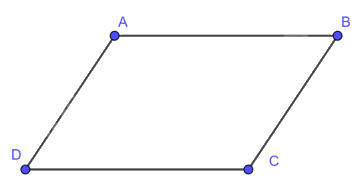
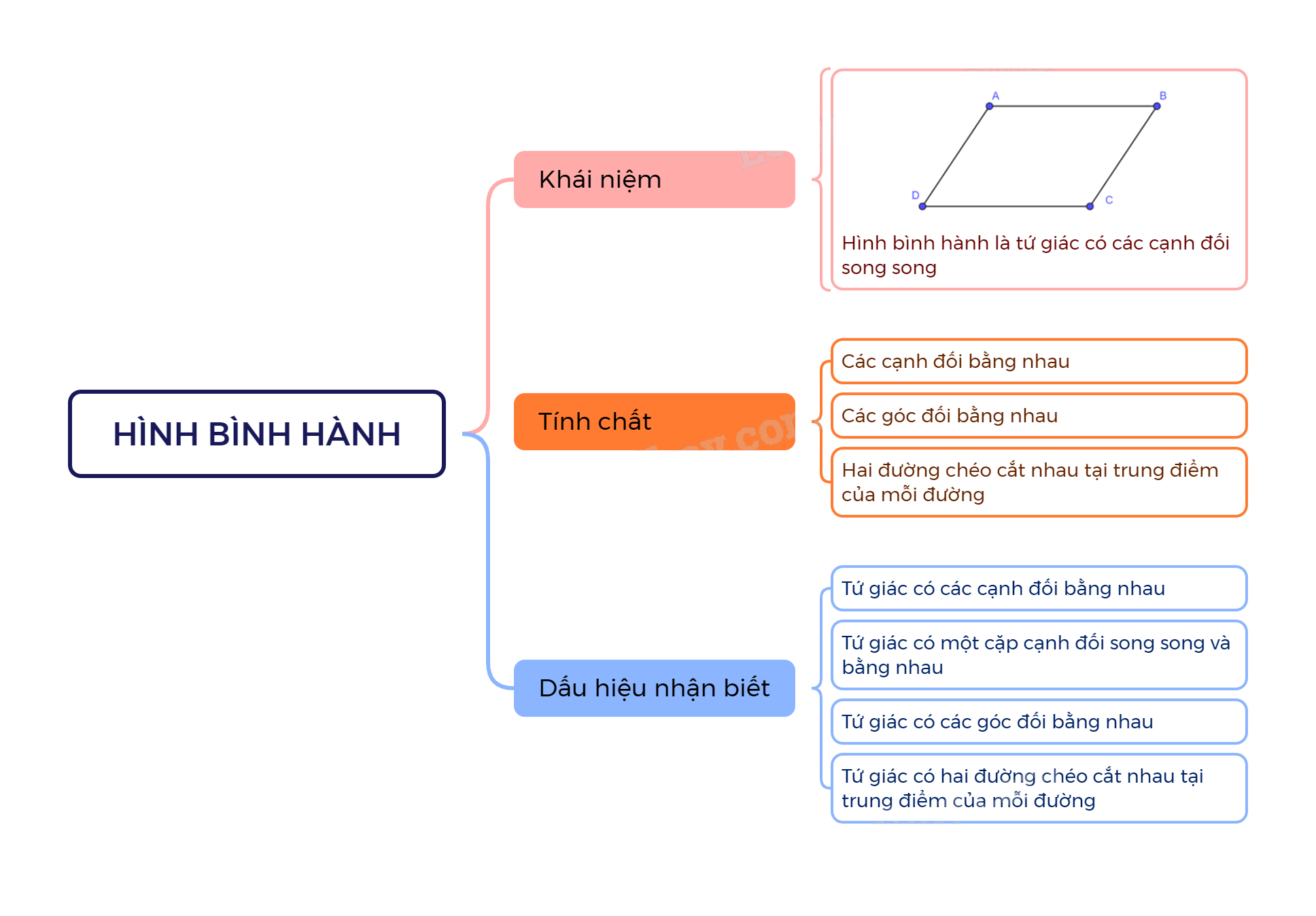
Hình bình hành là tứ giác có các cạnh đối song song.
2. Tính chất
Trong hình bình hành:
- Các cạnh đối bằng nhau;
- Các góc đối bằng nhau;
- Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
3. Dấu hiệu nhận biết
- Tứ giác có các cạnh đối bằng nhau là một hình bình hành.
- Tứ giác có một cặp cạnh đối song song và bằng nhau là một hình bình hành.
- Tứ giác có các góc đối bằng nhau là một hình bình hành.
- Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là một hình bình hành.
Ví dụ:
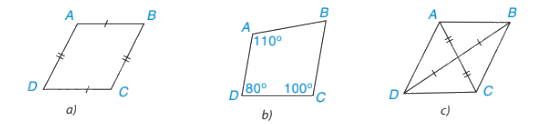
Hình a và c là hình bình hành do:
Hình a có các cặp cạnh đối bằng nhau.
Hình b có các đường chéo cắt nhau tại trung điểm của mỗi đường.
Hình bình hành là một trong những hình học cơ bản và quan trọng trong chương trình Toán 8. Việc nắm vững lý thuyết về hình bình hành không chỉ giúp học sinh giải quyết các bài tập trong sách giáo khoa mà còn là nền tảng cho việc học các kiến thức hình học nâng cao hơn.
Hình bình hành là hình tứ giác có hai cặp cạnh đối song song. Nói cách khác, nếu tứ giác ABCD có AB // CD và AD // BC thì ABCD là hình bình hành.
Hình bình hành có những tính chất quan trọng sau:
Có những dấu hiệu sau để nhận biết một tứ giác là hình bình hành:
Lý thuyết hình bình hành được ứng dụng rộng rãi trong giải toán hình học, đặc biệt là trong việc chứng minh các tính chất liên quan đến các hình tứ giác khác như hình chữ nhật, hình thoi, hình vuông. Việc hiểu rõ các tính chất và dấu hiệu nhận biết của hình bình hành giúp học sinh tiếp cận và giải quyết các bài toán một cách hiệu quả.
Bài tập 1: Cho hình bình hành ABCD. Gọi E là trung điểm của AB. Đường thẳng DE cắt BC tại F. Chứng minh rằng BF = FC.
Giải:
Để hiểu sâu hơn về hình bình hành, bạn có thể tìm hiểu thêm về các loại hình bình hành đặc biệt như hình chữ nhật, hình thoi, hình vuông. Mỗi loại hình này đều có những tính chất riêng biệt và ứng dụng trong giải toán.
Để nắm vững lý thuyết hình bình hành, bạn nên luyện tập thường xuyên các bài tập trong sách giáo khoa và các tài liệu tham khảo khác. Hãy cố gắng giải thích các bước giải một cách rõ ràng và logic để hiểu rõ bản chất của vấn đề.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về lý thuyết hình bình hành SGK Toán 8. Chúc bạn học tập tốt!