Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho bài 3.3 trang 58 sách giáo khoa Toán 8. Chúng tôi sẽ giúp bạn hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Giaitoan.edu.vn là nền tảng học toán online uy tín, cung cấp đầy đủ các bài giải, lý thuyết và bài tập Toán từ lớp 6 đến lớp 12.
Cho tam giác ABC có
Đề bài
Cho tam giác ABC có \(AB = 9cm,AC = 12cm,BC = 15cm.\)
a) Chứng minh tam giác ABC vuông tại A.
b) Trên tia đối của tia AB, lấy điểm D sao cho \(AD = 5cm.\) Tính độ dài CD.
Phương pháp giải - Xem chi tiết
a) Sử dụng định lí Pythagore đảo
b) Sử dụng định lí Pythagore để tính độ dài CD.
Lời giải chi tiết
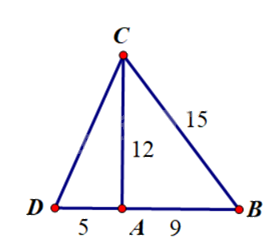
a) Ta có \(A{B^2} + A{C^2} = {9^2} + {12^2} = 225 = {15^2} = B{C^2}\)
Tam giác ABC vuông tại A (định lí Pythagore đảo).
b) Xét tam giác ABC vuông tại A suy ra \(AC \bot BD \Rightarrow \widehat {DAC} = {90^0}\)
Xét tam giác ADC vuông tại A có:
\(A{D^2} + A{C^2} = D{C^2}\)(định lí Pythagore)
\( \Rightarrow DC = \sqrt {{{12}^2} + {5^2}} = 13cm.\)
Bài 3.3 trang 58 SGK Toán 8 thuộc chương trình đại số, tập trung vào việc vận dụng các kiến thức về hình chữ nhật để giải quyết các bài toán thực tế. Để giải bài này, học sinh cần nắm vững các tính chất của hình chữ nhật, đặc biệt là tính chất về các cạnh đối song song và bằng nhau, các góc vuông, và đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Bài tập 3.3 thường yêu cầu học sinh chứng minh một tứ giác là hình chữ nhật dựa trên các điều kiện cho trước. Các điều kiện này có thể là:
Để giải bài 3.3 trang 58 SGK Toán 8 một cách hiệu quả, bạn có thể làm theo các bước sau:
Đề bài: Cho tứ giác ABCD có AB = CD, AD = BC. Chứng minh rằng ABCD là hình chữ nhật.
Lời giải:
Xét hai tam giác ABD và CDB, ta có:
Do đó, tam giác ABD = tam giác CDB (c-c-c). Suy ra ∠ABD = ∠CDB (hai góc tương ứng).
Vì ∠ABD = ∠CDB, mà hai góc này ở vị trí so le trong tạo bởi đường thẳng BD và hai đường thẳng AB, CD nên AB // CD.
Tương tự, xét hai tam giác ADB và CBD, ta có:
Do đó, tam giác ADB = tam giác CBD (c-c-c). Suy ra ∠ADB = ∠CBD (hai góc tương ứng).
Vì ∠ADB = ∠CBD, mà hai góc này ở vị trí so le trong tạo bởi đường thẳng BD và hai đường thẳng AD, BC nên AD // BC.
Vậy, tứ giác ABCD có AB // CD và AD // BC, do đó ABCD là hình bình hành.
Để chứng minh ABCD là hình chữ nhật, ta cần chứng minh một trong các góc của hình bình hành bằng 90 độ. Ví dụ, nếu ∠A = 90 độ, thì ABCD là hình chữ nhật.
Để củng cố kiến thức về hình chữ nhật và các bài toán liên quan, bạn có thể tham khảo thêm các bài tập sau:
Để học tốt môn Toán 8, bạn cần:
Bài 3.3 trang 58 SGK Toán 8 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hình chữ nhật và các tính chất của nó. Hy vọng với hướng dẫn chi tiết này, bạn sẽ giải bài tập một cách dễ dàng và hiệu quả. Chúc bạn học tốt!