Chào mừng các em học sinh đến với bài giải chi tiết bài 3.34 trang 88 SGK Toán 8. Tại giaitoan.edu.vn, chúng tôi cung cấp phương pháp giải bài tập Toán 8 một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Bài 3.34 thuộc chương trình Toán 8, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế. Chúng tôi sẽ hướng dẫn các em từng bước, từ việc phân tích đề bài đến việc đưa ra lời giải chính xác.
Năm 2019, vệ tinh Tsubame của Nhật Bản được Tổ chức Kỉ lục thế giới
Đề bài
Năm 2019, vệ tinh Tsubame của Nhật Bản được Tổ chức Kỉ lục thế giới Guinness ghi nhận là vệ tinh quan sát Trái Đất ở quỹ đạo thấp nhất. Trong Hình 3.90, vệ tinh Rsubame quan sát mặt đất ở vị trí \(A\) và có độ cao cách bề mặt Trái Đất là \(AB\). Tầm quan sát tối đa của vệ tinh Tsubame là đoạn thẳng \(AC\) có độ dài bằng 1470 km (từ vị trí \(A\), vệ tinh có thể quan sát thấy những nơi trên Trái Đất cách \(A\) không quá 1470 km). Cho biết ba điểm \(A,B,O\) thẳng hàng, bán kính Trái Đất là \(R = OB = OC = 6370km\) và \(AC\) vuông góc với \(OC\). Tính độ cao \(AB\) của vệ tinh Tsubame so với mặt đất theo kilomet (làm tròn kết quả đến hàng phần mười).
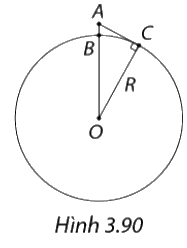
Phương pháp giải - Xem chi tiết
Áp dụng định lý Pythagore để tính độ cao \(AB\) của vệ tinh Tsubame so với mặt đất theo kilomet (làm tròn kết quả đến hàng phần mười).
Lời giải chi tiết
Độ cao \(AB\) của vệ tinh Tsubame so với mặt đất là:
\(\begin{array}{l}A{B^2} = A{C^2} + O{C^2}\\ = > AB = \sqrt {A{C^2} + O{C^2}} = \sqrt {{{\left( {1470} \right)}^2} + {{\left( {6370} \right)}^2}} = 6537,4\end{array}\)
Bài 3.34 trang 88 SGK Toán 8 là một bài toán yêu cầu học sinh vận dụng kiến thức về hình học, cụ thể là các tính chất của hình thang cân. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản và các định lý liên quan.
Trước khi đi vào giải bài, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu. Bài 3.34 thường yêu cầu chứng minh một tính chất nào đó của hình thang cân hoặc tính toán các yếu tố liên quan đến hình thang cân như độ dài đường trung bình, chiều cao, góc,…
(Giả sử đề bài yêu cầu chứng minh đường trung bình của hình thang cân chia hình thang thành hai phần có diện tích bằng nhau)
Ngoài bài 3.34, còn rất nhiều bài tập tương tự liên quan đến hình thang cân. Để giải các bài tập này, các em cần:
Để củng cố kiến thức, các em có thể tự giải các bài tập sau:
Bài 3.34 trang 88 SGK Toán 8 là một bài toán quan trọng giúp các em hiểu sâu hơn về hình thang cân và các tính chất của nó. Hy vọng với lời giải chi tiết và phương pháp giải mà giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn trong việc giải các bài tập Toán 8.