Chào mừng các em học sinh đến với bài giải chi tiết mục 1 trang 17, 18 Sách Giáo Khoa Toán 8. Tại giaitoan.edu.vn, chúng tôi cung cấp các lời giải bài tập Toán 8 được trình bày rõ ràng, dễ hiểu, giúp các em tự tin hơn trong việc học tập.
Mục tiêu của chúng tôi là hỗ trợ các em học sinh nắm vững kiến thức Toán học, rèn luyện kỹ năng giải bài tập và đạt kết quả tốt nhất trong các kỳ thi.
Cho hình vuông ABCD như Hình 1.8.
Trong các khẳng định sau đây, khẳng định nào đúng?
a) \(\left( {u - 1} \right)\left( {v - 1} \right) = uv - u - v + 1\) là một đồng nhất thức
b) \({\left( {a + b} \right)^2} = {a^2} + {b^2}\) là một đồng nhất thức.
Phương pháp giải:
Kiểm tra xem VT và VP có bằng nhau hay không? Nếu giá trị của hai vế luôn bằng nhau tại mọi giá trị thì ta có một đồng nhất thức ( hay hằng đẳng thức).
Lời giải chi tiết:
a) Ta có \(VT = u\left( {v - 1} \right) - 1\left( {v - 1} \right) = uv - u - v + 1 = VP\)
Nên \(\left( {u - 1} \right)\left( {v - 1} \right) = uv - u - v + 1\) là một đồng nhất thức
Vậy khẳng định a) là khẳng định đúng
b) Ta có \(VT = \left( {a + b} \right)\left( {a + b} \right) = aa + ab + ab + bb = {a^2} + 2ab + {b^2} \ne VP\)
\({\left( {a + b} \right)^2} = {a^2} + {b^2}\) không phải là một đồng nhất thức
Vậy khẳng định b) là khẳng định sai.
Cho hình vuông ABCD như Hình 1.8. 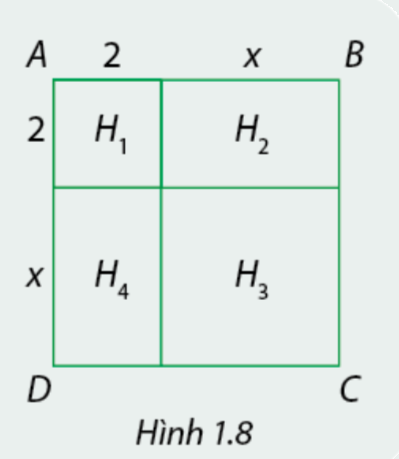
a) Tính độ dài AB, từ đó tính diện tích hình vuông ABCD.
b) Tính tổng diện tích của các hình \({H_1},{H_2},{H_3}\) và \({H_4}\).
c) Dựa vào câu a và câu b, hãy giải thích vì sao với mọi giá trị của \(x\) ta luôn có \({\left( {x + 2} \right)^2} = {x^2} + 4x + 4\)
Phương pháp giải:
a) Viết biểu thức biểu diễn độ dài AB, tính diện tích hình vuông theo công thức
b) Tính tổng diện tích của các hình \({H_1},{H_2},{H_3}\) và \({H_4}\).
c) Dựa vào câu a) và câu b).
Lời giải chi tiết:
a) Ta thấy \(AB = 2 + x\)
Diện tích hình vuông ABCD là : \({S_{ABCD}} = \left( {2 + x} \right).\left( {2 + x} \right) = {\left( {2 + x} \right)^2}\)
b) Ta có:
\({S_{{H_1}}} = 2.2 = 4;{S_{{H_2}}} = x.x = {x^2};{S_{{H_3}}} = x.x = {x^2};{S_{{H_4}}} = 2x\).
Tổng diện tích của các hình \({H_1},{H_2},{H_3}\) và \({H_4}\) là : \({S_{{H_1}}} + {S_{{H_2}}} + {S_{{H_3}}} + {S_{{H_4}}} = {x^2} + 4x + 4\)
c) Ta thấy tổng diện tích của các hình \({H_1},{H_2},{H_3}\) và \({H_4}\) chính là \({S_{ABCD}}\)
nên ta luôn có \({\left( {x + 2} \right)^2} = {x^2} + 4x + 4\) ( dpcm).
Cho hình vuông ABCD như Hình 1.8. 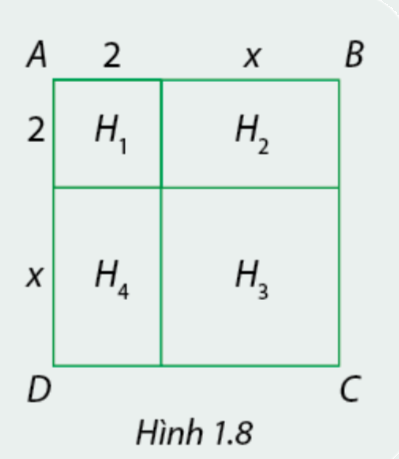
a) Tính độ dài AB, từ đó tính diện tích hình vuông ABCD.
b) Tính tổng diện tích của các hình \({H_1},{H_2},{H_3}\) và \({H_4}\).
c) Dựa vào câu a và câu b, hãy giải thích vì sao với mọi giá trị của \(x\) ta luôn có \({\left( {x + 2} \right)^2} = {x^2} + 4x + 4\)
Phương pháp giải:
a) Viết biểu thức biểu diễn độ dài AB, tính diện tích hình vuông theo công thức
b) Tính tổng diện tích của các hình \({H_1},{H_2},{H_3}\) và \({H_4}\).
c) Dựa vào câu a) và câu b).
Lời giải chi tiết:
a) Ta thấy \(AB = 2 + x\)
Diện tích hình vuông ABCD là : \({S_{ABCD}} = \left( {2 + x} \right).\left( {2 + x} \right) = {\left( {2 + x} \right)^2}\)
b) Ta có:
\({S_{{H_1}}} = 2.2 = 4;{S_{{H_2}}} = x.x = {x^2};{S_{{H_3}}} = x.x = {x^2};{S_{{H_4}}} = 2x\).
Tổng diện tích của các hình \({H_1},{H_2},{H_3}\) và \({H_4}\) là : \({S_{{H_1}}} + {S_{{H_2}}} + {S_{{H_3}}} + {S_{{H_4}}} = {x^2} + 4x + 4\)
c) Ta thấy tổng diện tích của các hình \({H_1},{H_2},{H_3}\) và \({H_4}\) chính là \({S_{ABCD}}\)
nên ta luôn có \({\left( {x + 2} \right)^2} = {x^2} + 4x + 4\) ( dpcm).
Trong các khẳng định sau đây, khẳng định nào đúng?
a) \(\left( {u - 1} \right)\left( {v - 1} \right) = uv - u - v + 1\) là một đồng nhất thức
b) \({\left( {a + b} \right)^2} = {a^2} + {b^2}\) là một đồng nhất thức.
Phương pháp giải:
Kiểm tra xem VT và VP có bằng nhau hay không? Nếu giá trị của hai vế luôn bằng nhau tại mọi giá trị thì ta có một đồng nhất thức ( hay hằng đẳng thức).
Lời giải chi tiết:
a) Ta có \(VT = u\left( {v - 1} \right) - 1\left( {v - 1} \right) = uv - u - v + 1 = VP\)
Nên \(\left( {u - 1} \right)\left( {v - 1} \right) = uv - u - v + 1\) là một đồng nhất thức
Vậy khẳng định a) là khẳng định đúng
b) Ta có \(VT = \left( {a + b} \right)\left( {a + b} \right) = aa + ab + ab + bb = {a^2} + 2ab + {b^2} \ne VP\)
\({\left( {a + b} \right)^2} = {a^2} + {b^2}\) không phải là một đồng nhất thức
Vậy khẳng định b) là khẳng định sai.
Mục 1 của chương trình Toán 8 thường tập trung vào việc ôn tập và mở rộng kiến thức về các phép toán cơ bản, các biểu thức đại số đơn giản, và các khái niệm về số thực. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Thông thường, mục 1 trang 17, 18 SGK Toán 8 sẽ bao gồm các bài tập sau:
Để giải các bài tập trong mục 1 trang 17, 18 SGK Toán 8 một cách hiệu quả, các em có thể áp dụng các phương pháp sau:
Bài tập: Tính giá trị của biểu thức: 2x + 3y với x = 1, y = 2.
Giải:
Thay x = 1 và y = 2 vào biểu thức, ta có:
2x + 3y = 2(1) + 3(2) = 2 + 6 = 8
Vậy, giá trị của biểu thức là 8.
Trong quá trình giải bài tập, các em cần lưu ý những điều sau:
Giaitoan.edu.vn là một website học toán online uy tín, cung cấp các bài giải chi tiết, dễ hiểu, và được cập nhật thường xuyên. Chúng tôi cam kết mang đến cho các em học sinh trải nghiệm học tập tốt nhất.
Ngoài ra, chúng tôi còn cung cấp các tài liệu học tập khác như:
Hãy truy cập giaitoan.edu.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích khác!
| Công thức | Mô tả |
|---|---|
| a2 - b2 = (a - b)(a + b) | Hiệu hai bình phương |
| (a + b)2 = a2 + 2ab + b2 | Bình phương của một tổng |
| (a - b)2 = a2 - 2ab + b2 | Bình phương của một hiệu |