Chào mừng các em học sinh đến với bài giải chi tiết mục 1 trang 67, 68 sách giáo khoa Toán 8. Tại giaitoan.edu.vn, chúng tôi cung cấp các lời giải bài tập Toán 8 được trình bày rõ ràng, dễ hiểu, giúp các em tự tin hơn trong việc học tập.
Mục tiêu của chúng tôi là hỗ trợ các em học sinh nắm vững kiến thức Toán 8, đồng thời rèn luyện kỹ năng giải bài tập một cách hiệu quả. Hãy cùng chúng tôi khám phá lời giải chi tiết cho từng bài tập trong mục này nhé!
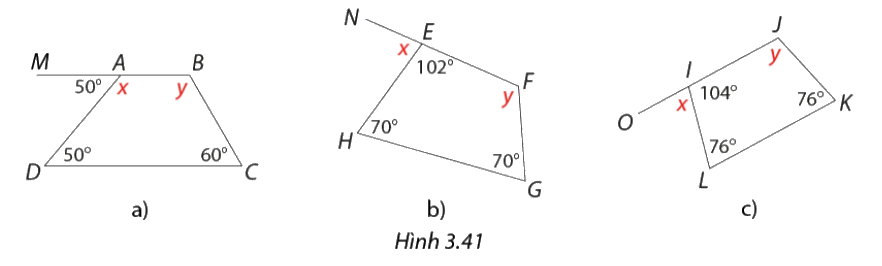
Trong các tứ giác ở Hình 3.41; tứ giác nào là hình thang, hình thang cân?
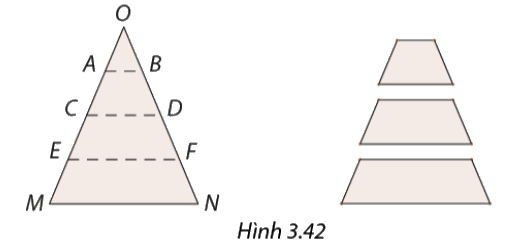
Mai cắt mảnh giấy hình tam giác cân \(OMN\) theo các đường song song với cạnh đáy (Hình 3.42). Vì sao các tứ giác thu được là hình thang cân?
Phương pháp giải:
Dựa vào tính chất của tam giác cân và hình thang cân để chứng minh các tứ giác thu được là hình thang cân.
Lời giải chi tiết:
Ta có tam giác \(OMN\) là tam giác cân nên có \(\widehat M = \widehat N\)
Mà \(MN//EF//CD//AB\) nên góc \(\widehat M = \widehat E = \widehat C = \widehat A\) và \(\widehat N = \widehat F = \widehat D = \widehat B\) (vì các góc này ở vị trí đồng vị)
Mà \(\widehat M = \widehat N\) nên \(\widehat M = \widehat E = \widehat C = \widehat A = \widehat N = \widehat F = \widehat D = \widehat B\)
Vậy các góc này sẽ tạo ra các tứ giác là hình thang cân.
Trong các tứ giác ở Hình 3.41; tứ giác nào là hình thang, hình thang cân? Tính các số đo góc \(x,y\) trong mỗi trường hợp.
Phương pháp giải:
Hình thang là tứ giác có hai cạnh đối song song. Hai cạnh song song được gọi là hai đáy, hai cạnh còn lại gọi là hai cạnh bên của hình thang.
Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
Lời giải chi tiết:
a) Tứ giác \(ABCD\) là hình thang vì hai góc kề một đáy không bằng nhau.
\(x = 180^\circ - 50^\circ = 130^\circ \)
\(y = 360^\circ - \left( {130^\circ + 50^\circ + 60^\circ } \right) = 120^\circ \)
b) Tứ giác \(EFGH\) là hình thang cân vì cơ hai góc kề một đáy bằng nhau.
\(\begin{array}{l}x = 180^\circ - 102^\circ = 78^\circ \\y = 360^\circ - \left( {102^\circ + 70^\circ + 70^\circ } \right) = 118^\circ \end{array}\)
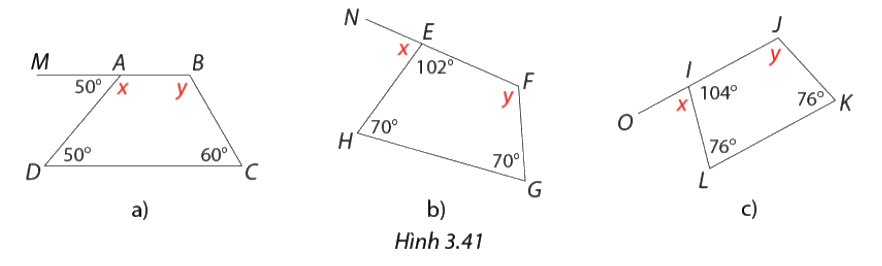
Trong các tứ giác ở Hình 3.41; tứ giác nào là hình thang, hình thang cân? Tính các số đo góc \(x,y\) trong mỗi trường hợp.
Phương pháp giải:
Hình thang là tứ giác có hai cạnh đối song song. Hai cạnh song song được gọi là hai đáy, hai cạnh còn lại gọi là hai cạnh bên của hình thang.
Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
Lời giải chi tiết:
a) Tứ giác \(ABCD\) là hình thang vì hai góc kề một đáy không bằng nhau.
\(x = 180^\circ - 50^\circ = 130^\circ \)
\(y = 360^\circ - \left( {130^\circ + 50^\circ + 60^\circ } \right) = 120^\circ \)
b) Tứ giác \(EFGH\) là hình thang cân vì cơ hai góc kề một đáy bằng nhau.
\(\begin{array}{l}x = 180^\circ - 102^\circ = 78^\circ \\y = 360^\circ - \left( {102^\circ + 70^\circ + 70^\circ } \right) = 118^\circ \end{array}\)
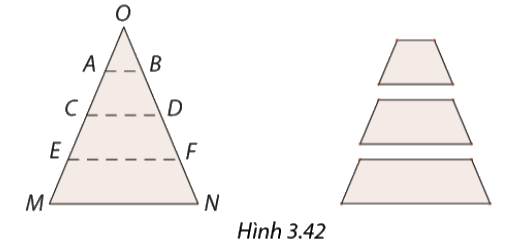
Mai cắt mảnh giấy hình tam giác cân \(OMN\) theo các đường song song với cạnh đáy (Hình 3.42). Vì sao các tứ giác thu được là hình thang cân?
Phương pháp giải:
Dựa vào tính chất của tam giác cân và hình thang cân để chứng minh các tứ giác thu được là hình thang cân.
Lời giải chi tiết:
Ta có tam giác \(OMN\) là tam giác cân nên có \(\widehat M = \widehat N\)
Mà \(MN//EF//CD//AB\) nên góc \(\widehat M = \widehat E = \widehat C = \widehat A\) và \(\widehat N = \widehat F = \widehat D = \widehat B\) (vì các góc này ở vị trí đồng vị)
Mà \(\widehat M = \widehat N\) nên \(\widehat M = \widehat E = \widehat C = \widehat A = \widehat N = \widehat F = \widehat D = \widehat B\)
Vậy các góc này sẽ tạo ra các tứ giác là hình thang cân.
Mục 1 trang 67, 68 SGK Toán 8 thường chứa các bài tập về các kiến thức cơ bản của chương trình đại số hoặc hình học. Để giải quyết các bài tập này một cách hiệu quả, học sinh cần nắm vững các định nghĩa, tính chất và công thức liên quan.
Thông thường, mục này sẽ tập trung vào một trong các chủ đề sau:
Để giúp các em học sinh giải bài tập một cách dễ dàng, chúng tôi sẽ trình bày chi tiết lời giải cho từng bài tập trong mục 1 trang 67, 68 SGK Toán 8.
Đề bài: Thu gọn đa thức sau: A = 3x2 + 2xy - 5x2 + 4xy - x.
Lời giải:
Đề bài: Phân tích đa thức thành nhân tử: B = x2 - 4x + 4.
Lời giải:
Sử dụng hằng đẳng thức (a - b)2 = a2 - 2ab + b2, ta có: B = (x - 2)2.
Luyện tập thường xuyên là yếu tố quan trọng để nắm vững kiến thức Toán 8. Hãy dành thời gian giải các bài tập trong SGK, sách bài tập và các đề thi thử để rèn luyện kỹ năng giải bài tập.
Kiến thức Toán 8 có ứng dụng rộng rãi trong thực tế, đặc biệt trong các lĩnh vực như khoa học, kỹ thuật, kinh tế và tài chính. Việc nắm vững kiến thức Toán 8 sẽ giúp bạn có lợi thế trong học tập và công việc sau này.
| Công thức | Mô tả |
|---|---|
| (a + b)2 | Bình phương của một tổng |
| (a - b)2 | Bình phương của một hiệu |
| a2 - b2 | Hiệu hai bình phương |
Hy vọng với những hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn trong việc giải các bài tập mục 1 trang 67, 68 SGK Toán 8. Chúc các em học tập tốt!