Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8. Bài viết này sẽ giúp bạn giải quyết triệt để các vấn đề trong mục 1 trang 37 SGK Toán 8, đồng thời cung cấp kiến thức nền tảng vững chắc.
Chúng tôi hiểu rằng việc học Toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Đối với mỗi chiếc lá phong trong hình (6.2,)
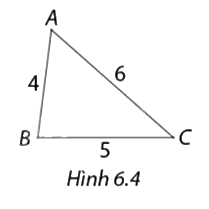
Trong hình 6.4, độ dài các đoạn thẳng được viết với cùng đơn vị đo. Tính các tỉ số \(\frac{{AB}}{{BC}},\frac{{BC}}{{AC}}\) và cho biết hai đoạn thẳng \(AB\) và \(BC\) có tỉ lệ với đoạn thẳng \(BC\) và \(AC\) không.
Phương pháp giải:
Tỉ số của hai đoạn thẳng AB và CD là tỉ số độ dài của chúng theo cùng một đơn vị đo, kí hiệu \(\frac{{AB}}{{CD}}\).
Hai đoạn thẳng AB và CD được gọi là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức \(\frac{{AB}}{{CD}} = \frac{{A'B'}}{{C'D'}}\) hay \(\frac{{AB}}{{A'B'}} = \frac{{CD}}{{C'D'}}\).
Lời giải chi tiết:
\(\begin{array}{l}\frac{{AB}}{{BC}} = \frac{4}{5} = 0,8\\\frac{{BC}}{{AC}} = \frac{5}{6} = 0,83\end{array}\)
Hai đoạn thẳng AB và BC không tỉ lệ với đoạn thẳng BC và AC bởi vì \(\frac{{AB}}{{BC}} \ne \frac{{BC}}{{AC}}\).
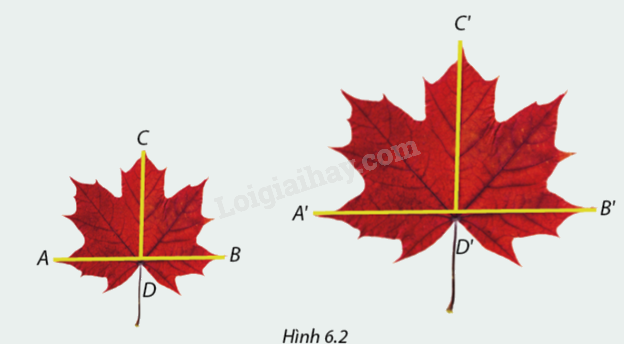
Đối với mỗi chiếc lá phong trong hình \(6.2,\) hãy đo chiều rộng \(AB;A'B'\) và chiều dài \(CD;C'D'\) (với đơn vị là centimét).
1. Tính tỉ số độ dài \(AB\) và \(CD.\)
2. Tính tỉ số độ dài \(A'B'\) và \(C'D'.\)
Em có nhận xét gì về hai tỉ số trên?
Phương pháp giải:
Đo chiều rộng \(AB;A'B'\) và chiều dài \(CD;C'D'\) (với đơn vị là centimét). Sau đó tính tỉ số độ dài \(AB\) và \(CD.\)\(A'B'\) và \(C'D'.\)
Lời giải chi tiết:
1. Tỉ số độ dài \(AB\) và \(CD\) là \(\frac{{AB}}{{CD}} = \frac{4}{3}\)
2. Tỉ số độ dài \(A'B'\) và \(C'D'\) là \(\frac{{A'B'}}{{C'D'}} = \frac{4}{3}\)
Quan sát tỉ số của các cặp đoạn thẳng ta thấy \(\frac{{AB}}{{CD}} = \frac{{A'B'}}{{C'D'}} = \frac{4}{3}\).
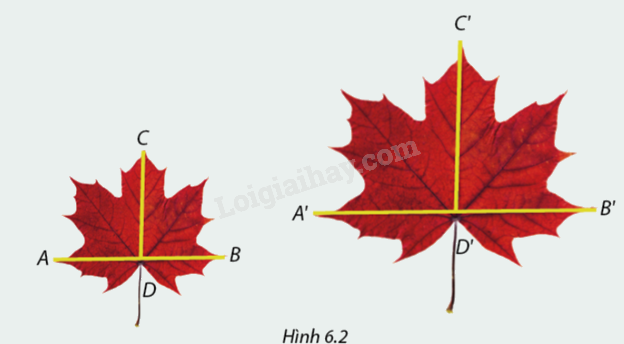
Đối với mỗi chiếc lá phong trong hình \(6.2,\) hãy đo chiều rộng \(AB;A'B'\) và chiều dài \(CD;C'D'\) (với đơn vị là centimét).
1. Tính tỉ số độ dài \(AB\) và \(CD.\)
2. Tính tỉ số độ dài \(A'B'\) và \(C'D'.\)
Em có nhận xét gì về hai tỉ số trên?
Phương pháp giải:
Đo chiều rộng \(AB;A'B'\) và chiều dài \(CD;C'D'\) (với đơn vị là centimét). Sau đó tính tỉ số độ dài \(AB\) và \(CD.\)\(A'B'\) và \(C'D'.\)
Lời giải chi tiết:
1. Tỉ số độ dài \(AB\) và \(CD\) là \(\frac{{AB}}{{CD}} = \frac{4}{3}\)
2. Tỉ số độ dài \(A'B'\) và \(C'D'\) là \(\frac{{A'B'}}{{C'D'}} = \frac{4}{3}\)
Quan sát tỉ số của các cặp đoạn thẳng ta thấy \(\frac{{AB}}{{CD}} = \frac{{A'B'}}{{C'D'}} = \frac{4}{3}\).
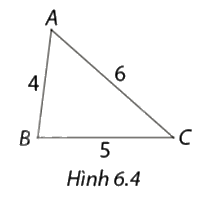
Trong hình 6.4, độ dài các đoạn thẳng được viết với cùng đơn vị đo. Tính các tỉ số \(\frac{{AB}}{{BC}},\frac{{BC}}{{AC}}\) và cho biết hai đoạn thẳng \(AB\) và \(BC\) có tỉ lệ với đoạn thẳng \(BC\) và \(AC\) không.
Phương pháp giải:
Tỉ số của hai đoạn thẳng AB và CD là tỉ số độ dài của chúng theo cùng một đơn vị đo, kí hiệu \(\frac{{AB}}{{CD}}\).
Hai đoạn thẳng AB và CD được gọi là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức \(\frac{{AB}}{{CD}} = \frac{{A'B'}}{{C'D'}}\) hay \(\frac{{AB}}{{A'B'}} = \frac{{CD}}{{C'D'}}\).
Lời giải chi tiết:
\(\begin{array}{l}\frac{{AB}}{{BC}} = \frac{4}{5} = 0,8\\\frac{{BC}}{{AC}} = \frac{5}{6} = 0,83\end{array}\)
Hai đoạn thẳng AB và BC không tỉ lệ với đoạn thẳng BC và AC bởi vì \(\frac{{AB}}{{BC}} \ne \frac{{BC}}{{AC}}\).
Mục 1 trang 37 SGK Toán 8 thường chứa các bài tập liên quan đến các kiến thức cơ bản về đa thức, phân thức đại số, phương trình bậc nhất một ẩn, và hệ phương trình bậc nhất hai ẩn. Việc nắm vững các kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo của môn Toán 8.
Thông thường, mục này sẽ bao gồm các dạng bài tập sau:
Để giải tốt các bài tập trong mục này, bạn cần nắm vững các kiến thức sau:
Ví dụ 1: Thu gọn đa thức sau: A = 3x2 - 5x + 2 + x2 - 3x - 1
Giải:
A = (3x2 + x2) + (-5x - 3x) + (2 - 1)
A = 4x2 - 8x + 1
Ví dụ 2: Giải phương trình sau: 2x - 3 = 5
Giải:
2x = 5 + 3
2x = 8
x = 4
Việc giải bài tập trong Mục 1 trang 37 SGK Toán 8 không chỉ giúp bạn nắm vững kiến thức mà còn rèn luyện kỹ năng giải toán. Đây là một bước chuẩn bị quan trọng để bạn có thể tự tin giải quyết các bài toán khó hơn trong tương lai.
Ngoài SGK Toán 8, bạn có thể tham khảo thêm các nguồn tài liệu sau:
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong Mục 1 trang 37 SGK Toán 8. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!