Chào mừng các em học sinh đến với bài giải chi tiết bài 6.23 trang 55 SGK Toán 8. Bài học này thuộc chương trình Toán 8, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp những lời giải chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Trong Hình 6.57, độ dài cạnh mỗi ô vuông lớn là \(5\) đơn vị
Đề bài
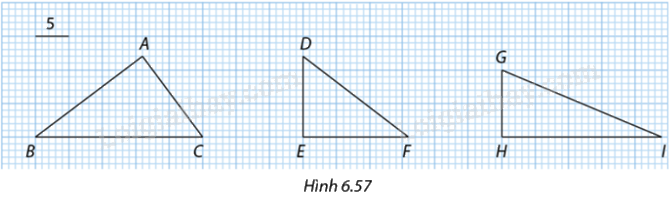
Trong Hình 6.57, độ dài cạnh mỗi ô vuông lớn là \(5\) đơn vị. Tính độ dài các cạnh của \(\Delta ABC,\Delta DEF,\Delta GHI\) và cho biết các tam giác nào đồng dạng với nhau. Viết kí hiệu của sự đồng dạng đó và xác định tỉ số đồng dạng.
Phương pháp giải - Xem chi tiết
Tính các cạnh của tam giác sau đó áp dụng trường hợp đồng dạng cạnh cạnh cạnh để chứng minh.
Lời giải chi tiết
Xét tam giác \(ABC\), có:
\(BC = 25\)
\(AC = \sqrt {{{12}^2} + {9^2}} = 15\)
\(AB = \sqrt {{{16}^2} + {{12}^2}} = 20\)
Xét tam giác \(DEF\), có:
\(EF = 16\)
\(DE = 12\)
\(DF = \sqrt {{{16}^2} + {{12}^2}} = 20\)
Xét tam giác \(GHI\), có:
\(\begin{array}{l}HG = 10\\HI = 24\\GI = \sqrt {{{10}^2} + {{24}^2}} = 26\end{array}\)
Vậy ta thấy \(\Delta ABC\) ∽ \(\Delta EFD\), có tỉ số đồng dạng:
\(\begin{array}{l}\frac{{AC}}{{DE}} = \frac{{15}}{{12}} = \frac{5}{4}\\\frac{{AB}}{{EF}} = \frac{{20}}{{16}} = \frac{5}{4}\\\frac{{BC}}{{DF}} = \frac{{25}}{{20}} = \frac{5}{4}\\ = > \frac{{AC}}{{DE}} = \frac{{AB}}{{EF}} = \frac{{BC}}{{DF}} = \frac{5}{4}\end{array}\)
Bài 6.23 trang 55 SGK Toán 8 thuộc chương trình đại số, thường liên quan đến việc giải phương trình bậc nhất một ẩn hoặc các bài toán về ứng dụng phương trình. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản sau:
Để cung cấp một lời giải chi tiết, chúng ta cần biết nội dung cụ thể của bài 6.23. Tuy nhiên, dựa trên kinh nghiệm giải các bài toán tương tự, chúng ta có thể đưa ra một quy trình giải chung:
Giả sử bài 6.23 có nội dung như sau: Một người đi xe máy từ A đến B với vận tốc 40km/h. Sau khi đi được 1 giờ, người đó tăng vận tốc lên 50km/h và đến B muộn hơn 30 phút so với dự kiến. Tính quãng đường AB.
Giải:
Gọi x là quãng đường AB (km). Thời gian dự kiến đi từ A đến B là x/40 (giờ). Thời gian thực tế đi từ A đến B là 1 + (x-40)/50 (giờ). Theo đề bài, thời gian thực tế nhiều hơn thời gian dự kiến 30 phút (0.5 giờ). Ta có phương trình:
1 + (x-40)/50 = x/40 + 0.5
Giải phương trình, ta được x = 200 (km). Vậy quãng đường AB là 200km.
Để củng cố kiến thức và kỹ năng giải bài tập, các em có thể luyện tập thêm với các bài tập tương tự trong SGK Toán 8 và các tài liệu tham khảo khác. Hãy chú trọng vào việc hiểu rõ bản chất của bài toán và áp dụng các phương pháp giải phù hợp.
Giaitoan.edu.vn cam kết cung cấp những bài giải chi tiết, chính xác và dễ hiểu, giúp các em học sinh nắm vững kiến thức Toán học và đạt kết quả tốt trong học tập. Hãy truy cập website của chúng tôi để khám phá thêm nhiều tài liệu học tập hữu ích khác.
| Chủ đề | Nội dung |
|---|---|
| Lý thuyết | Phương trình bậc nhất một ẩn |
| Phương pháp | Giải phương trình, lập phương trình |
| Bài tập | Giải bài 6.23 trang 55 SGK Toán 8 |