Chào mừng các em học sinh đến với bài học về lý thuyết Diện tích xung quanh của hình chóp tam giác đều và hình chóp tứ giác đều trong chương trình Toán 8. Bài học này sẽ cung cấp cho các em những kiến thức cơ bản và quan trọng nhất về chủ đề này.
Chúng ta sẽ cùng nhau tìm hiểu công thức tính diện tích xung quanh, cách áp dụng công thức vào giải bài tập, và những lưu ý quan trọng khi làm bài. Hãy cùng bắt đầu nhé!
Công thức tính diện tích xung quanh của hình chóp tam giác đều và hình chóp tứ giác đều
Công thức tính diện tích xung quanh của hình chóp tam giác đều và hình chóp tứ giác đều
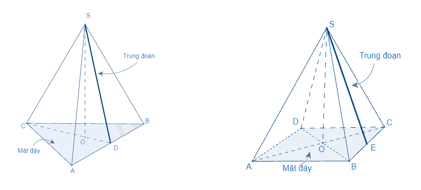
Diện tích xung quanh, kí hiệu là \({S_{xq}}\) của hình chóp tam giác đều hoặc hình chóp tứ giác đều được tính theo công thức:
\({S_{xq}} = p.d\)
Với p là nửa chu vi đáy và d là đường cao của mặt bên kẻ từ đỉnh của hình chóp đó.
Ví dụ:
Cho hình chóp tứ giác đều sau:
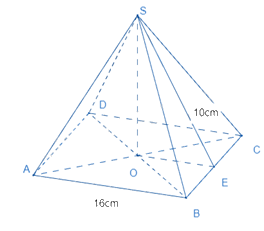
Diện tích xung quanh của hình chóp là: \({S_{xq}} = 4.\frac{1}{2}.10.16 = 320(c{m^2})\)
Diện tích xung quanh của hình chóp là tổng diện tích của tất cả các mặt bên của hình chóp. Để tính diện tích xung quanh, chúng ta cần hiểu rõ về các yếu tố của hình chóp và công thức tính diện tích của từng mặt bên.
Hình chóp tam giác đều là hình chóp có đáy là tam giác đều và các mặt bên là các tam giác cân bằng nhau. Các yếu tố quan trọng của hình chóp tam giác đều bao gồm:
Công thức tính diện tích xung quanh của hình chóp tam giác đều là:
Sxq = p.l
Trong đó:
Hình chóp tứ giác đều là hình chóp có đáy là hình vuông và các mặt bên là các tam giác cân bằng nhau. Các yếu tố quan trọng của hình chóp tứ giác đều bao gồm:
Công thức tính diện tích xung quanh của hình chóp tứ giác đều là:
Sxq = p.l
Trong đó:
Trong cả hai loại hình chóp trên, chiều cao (h), trung đoạn (l) và cạnh đáy (a) có mối quan hệ mật thiết với nhau. Chúng ta có thể sử dụng định lý Pitago để tìm mối liên hệ này:
l2 = h2 + (a/2)2 (đối với hình chóp tam giác đều)
l2 = h2 + (a/2)2 (đối với hình chóp tứ giác đều)
Bài 1: Tính diện tích xung quanh của hình chóp tam giác đều có cạnh đáy là 5cm và trung đoạn là 8cm.
Giải:
Nửa chu vi đáy là: p = 3.5/2 = 7.5cm
Diện tích xung quanh là: Sxq = 7.5.8 = 60cm2
Bài 2: Tính diện tích xung quanh của hình chóp tứ giác đều có cạnh đáy là 6cm và trung đoạn là 10cm.
Giải:
Nửa chu vi đáy là: p = 2.6 = 12cm
Diện tích xung quanh là: Sxq = 12.10 = 120cm2
Hy vọng bài học này đã giúp các em hiểu rõ hơn về lý thuyết Diện tích xung quanh của hình chóp tam giác đều và hình chóp tứ giác đều. Chúc các em học tốt!