Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 của giaitoan.edu.vn. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Ở bài viết này, chúng ta sẽ cùng nhau đi sâu vào giải chi tiết các bài tập trong mục 2 trang 14, 15, 16 SGK Toán 8. Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hàm số
Hãy trả lời câu hỏi trong phần Khởi động.
Các tác phẩm của danh hoạc Leonardo da Vinci không chỉ đặc sắc bởi tính nghệ thuật mà còn mang nhiều vẻ đẹp toán học. Khi vẽ người, ông quan tâm đến tỉ lệ chính xác của cơ thể nhằm tăng tính chân thức cho bức tranh. Ông đã vẽ bức tranh “Vitruvian Man” thể hiện ý tưởng về tỉ lệ hoàn mĩ của cơ thể người (Hình 5.19).
Trong bức tranh này, chiều cao của một người bằng tám lần chiều cao của đầu người đó (khoảng cách từ cằm đến đỉnh đầu). Đã từ lâu, đây là một quy chuẩn trong hội họa và sau này được nghiên cứu, phát triển ứng dụng trong kiến trúc
Từ bức tranh này, có thể biểu diễn mối quan hệ giữa chiều dài sải tay và chiều cao của một người như nào.
Phương pháp giải:
Dựa vào định nghĩa hàm số bậc nhất và mối quan hệ của chiều dài sải tay và chiều cao của một người để biểu diễn dưới dạng \(y = ax + b\)
Lời giải chi tiết:
Dựa vào bức tranh ta thấy chiều dài sải tay gấp ba lần chiều cao đầu của người đó. Gọi chiều dài sải tay là x thì chiều cao đầu người đó là \(\frac{1}{3}x\).
Mà chiều cao của một người bằng tám lần chiều cao của đầu người đó:
\(y = 8.\frac{1}{3}x = \frac{8}{3}x\)
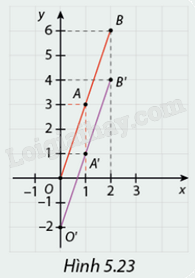
Hình 5.23 biểu diễn các điểm \(O\left( {0;0} \right),A\left( {1;3} \right),B\left( {2;6} \right)\) và \(O'\left( {0; - 2} \right),A'\left( {1;1} \right),B'\left( {2;4} \right)\) trên mặt phẳng tọa độ.
a) Nhận xét về sự song song giữa \(OA\) và \(O'A'\); \(AB\) và \(A'B'\).
b) Đồ thị hàm số \(y = 3x\) có đi qua các điểm \(O,A,B\) không?
c) Đồ thị hàm số \(y = 3x - 2\) có đi qua các điểm \(O',A',B'\) không?
Phương pháp giải:
Với bất kì hoành độ x nào thì tung độ y của điểm thuộc đồ thị hàm số \(y = 3x - 2\) cũng nhỏ hơn hai đơn vị so với tung độ y tương ứng của điểm thuộc đồ thị hàm số \(y = 3x\). Đồ thị của hàm số \(y = 3x\) là đường thẳng đi qua gốc tọa độ \(O\left( {0;0} \right)\) và điểm \(A\left( {1;3} \right)\). Từ đó ta thấy rằng đồ thị hàm số \(y = 3x - 2\) là một đường thẳng song song với đường thẳng \(y = 3x\).
Lời giải chi tiết:
a) Ta có:
\(\begin{array}{l}OB//O'B'\\ = > OA//O'A',AB//A'B'\end{array}\)
Mà ta thấy điểm O và O’ , điểm A va A’, điểm B và B’ đều có tung độ cách nhau 2 đơn vị với hoành độ lần lượt là 0, 1, 2.
b) Ta có:
Với \(x = 0\) thì \(y = 3.0 = 0\) => đồ thị hàm số \(y = 3x\) đi qua O
Với \(x = 1\) thì \(y = 3.1 = 3\) => đồ thị hàm số \(y = 3x\) đi qua A
Với \(x = 2\) thì \(y = 3.2 = 6\) => đồ thì hàm số \(y = 3x\) đi qua
c) Ta có:
Với \(x = 0\) thì \(y = 3.0 - 2 = - 2\) => đồ thị hàm số \(y = 3x - 2\) đi qua O’
Với \(x = 1\) thì \(y = 3.1 - 2 = 1\) => đồ thị hàm số \(y = 3x - 2\) đi qua A’
Với \(x = 2\) thì \(y = 3.2 - 2 = 4\) => đồ thị hàm số \(y = 3x - 2\) đi qua B’
Vẽ đồ thị của các hàm số sau:
a) \(y = 3x + 1\)
b) \(y = - 2x + 3\)
Phương pháp giải:
Để vẽ đồ thị hàm số \(y = ax + b\left( {a \ne 0} \right)\), ta chỉ cần xác định hai điểm phân biệt thuộc đồ thị rồi vẽ đường thẳng đi qua hai điểm đó.
Lời giải chi tiết:
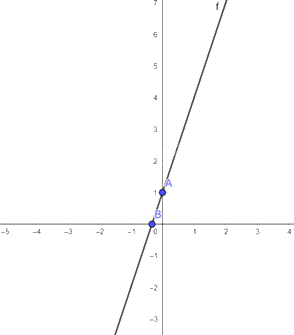
a) \(y = 3x + 1\)
Vẽ hệ trục tọa độ \(Oxy\).
Cho \(x = 0\) ta được \(y = 1\)
Cho \(y = 0\) ta được \(x = \frac{{ - 1}}{3}\)
Đồ thì của hàm số \(y = 3x + 1\) là đường thẳng đi qua hai điểm \(A\left( {0;1} \right),B\left( {\frac{{ - 1}}{3};0} \right)\)
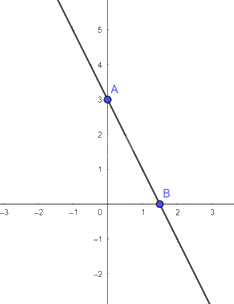
b) \(y = - 2x + 3\)
Vẽ hệ trục tọa độ \(Oxy\)
Cho \(x = 0\) ta được \(y = 3\)
Cho \(y = 0\) ta được \(x = \frac{3}{2}\)
Đồ thị của hàm số \(y = - 2x + 3\) là đường thẳng đi qua hai điểm \(A\left( {0;3} \right),B\left( {\frac{3}{2};0} \right)\)
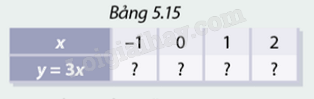
Cho hàm số \(y = 3x\).
a) Tìm các giá trị tương ứng của hàm số trong Bảng 5.15.
b) Vẽ một hệ trục tọa độ \(Oxy\) và đánh dấu các điểm biểu diễn các cặp giá trị \(\left( {x;y} \right)\) tương ứng trong Bảng 5.15.
c) Vẽ đường thẳng đi qua hai trong bốn điểm trên. Dùng thước thẳng kiểm tra xem đường thẳng này có đi qua hai điểm còn lại hay không.
d) Lấy thêm một cặp số \(\left( {x;y} \right)\), với x chọn tùy ý khác bốn giá trị ở trên. Đánh dấu điểm biểu diễn cặp số đó lên mặt phẳng tọa độ \(Oxy\). Dùng thước thẳng kiểm tra xem điểm vừa đánh dấu có thuộc đường thẳng đã vẽ ở câu c không.
Phương pháp giải:
Tìm các giá trị tương ứng trong bảng, dựa vào những giá trị đó vẽ hệ trục tọa độ \(Oxy\) biểu diễn các cặp giá trị tương ứng vừa tìm được
Vẽ đường thẳng đi qua hai trong bốn điểm trên. Dùng thước thẳng kiểm tra xem đường thẳng này có đi qua hai điểm còn lại không.
Lấy thêm một cặp số \(\left( {x;y} \right)\), với x chọn tùy ý khác bốn giá trị ở trên. Đánh dấu điểm biểu diễn cặp số đó lên mặt phẳng tọa độ \(Oxy\). Dùng thước thẳng kiểm tra xem điểm vừa đánh dấu có thuộc đường thẳng đã vẽ ở câu c không.
Lời giải chi tiết:
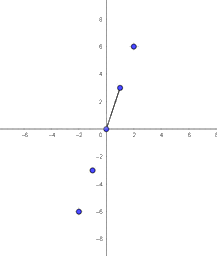
a) Các giá trị tương ứng của hàm số trong Bảng 5.15 là: \(\left( { - 1; - 3} \right),\left( {0;0} \right),\left( {1;3} \right),\left( {2;6} \right)\).
b) Vẽ hệ trục tọa độ \(Oxy\)
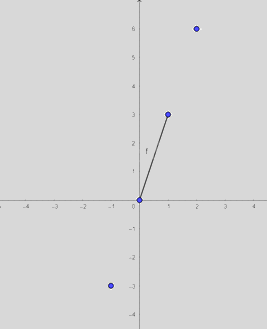
c) Vẽ đường thẳng đi qua 2 điểm. Dùng thước thẳng kiểm tra thấy đường thẳng này đi qua hai điểm còn lại.
d) Lấy cặp số \(\left( { - 2; - 6} \right)\). Đánh dấu vào hệ trục tọa độ \(Oxy\)
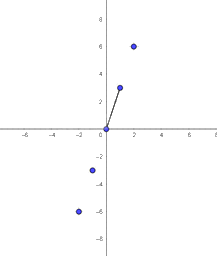
Dùng thước thẳng kiểm tra ta thấy điểm vừa đánh dấu thuộc đường thẳng đã vẽ ở câu c.
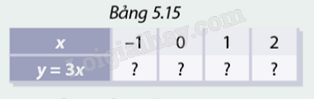
Cho hàm số \(y = 3x\).
a) Tìm các giá trị tương ứng của hàm số trong Bảng 5.15.
b) Vẽ một hệ trục tọa độ \(Oxy\) và đánh dấu các điểm biểu diễn các cặp giá trị \(\left( {x;y} \right)\) tương ứng trong Bảng 5.15.
c) Vẽ đường thẳng đi qua hai trong bốn điểm trên. Dùng thước thẳng kiểm tra xem đường thẳng này có đi qua hai điểm còn lại hay không.
d) Lấy thêm một cặp số \(\left( {x;y} \right)\), với x chọn tùy ý khác bốn giá trị ở trên. Đánh dấu điểm biểu diễn cặp số đó lên mặt phẳng tọa độ \(Oxy\). Dùng thước thẳng kiểm tra xem điểm vừa đánh dấu có thuộc đường thẳng đã vẽ ở câu c không.
Phương pháp giải:
Tìm các giá trị tương ứng trong bảng, dựa vào những giá trị đó vẽ hệ trục tọa độ \(Oxy\) biểu diễn các cặp giá trị tương ứng vừa tìm được
Vẽ đường thẳng đi qua hai trong bốn điểm trên. Dùng thước thẳng kiểm tra xem đường thẳng này có đi qua hai điểm còn lại không.
Lấy thêm một cặp số \(\left( {x;y} \right)\), với x chọn tùy ý khác bốn giá trị ở trên. Đánh dấu điểm biểu diễn cặp số đó lên mặt phẳng tọa độ \(Oxy\). Dùng thước thẳng kiểm tra xem điểm vừa đánh dấu có thuộc đường thẳng đã vẽ ở câu c không.
Lời giải chi tiết:
a) Các giá trị tương ứng của hàm số trong Bảng 5.15 là: \(\left( { - 1; - 3} \right),\left( {0;0} \right),\left( {1;3} \right),\left( {2;6} \right)\).
b) Vẽ hệ trục tọa độ \(Oxy\)
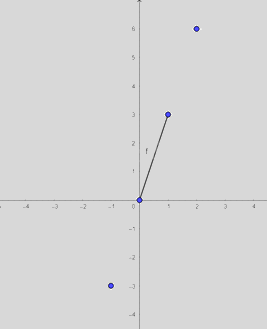
c) Vẽ đường thẳng đi qua 2 điểm. Dùng thước thẳng kiểm tra thấy đường thẳng này đi qua hai điểm còn lại.
d) Lấy cặp số \(\left( { - 2; - 6} \right)\). Đánh dấu vào hệ trục tọa độ \(Oxy\)
Dùng thước thẳng kiểm tra ta thấy điểm vừa đánh dấu thuộc đường thẳng đã vẽ ở câu c.
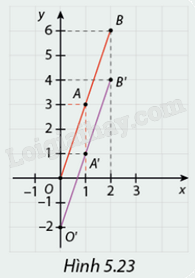
Hình 5.23 biểu diễn các điểm \(O\left( {0;0} \right),A\left( {1;3} \right),B\left( {2;6} \right)\) và \(O'\left( {0; - 2} \right),A'\left( {1;1} \right),B'\left( {2;4} \right)\) trên mặt phẳng tọa độ.
a) Nhận xét về sự song song giữa \(OA\) và \(O'A'\); \(AB\) và \(A'B'\).
b) Đồ thị hàm số \(y = 3x\) có đi qua các điểm \(O,A,B\) không?
c) Đồ thị hàm số \(y = 3x - 2\) có đi qua các điểm \(O',A',B'\) không?
Phương pháp giải:
Với bất kì hoành độ x nào thì tung độ y của điểm thuộc đồ thị hàm số \(y = 3x - 2\) cũng nhỏ hơn hai đơn vị so với tung độ y tương ứng của điểm thuộc đồ thị hàm số \(y = 3x\). Đồ thị của hàm số \(y = 3x\) là đường thẳng đi qua gốc tọa độ \(O\left( {0;0} \right)\) và điểm \(A\left( {1;3} \right)\). Từ đó ta thấy rằng đồ thị hàm số \(y = 3x - 2\) là một đường thẳng song song với đường thẳng \(y = 3x\).
Lời giải chi tiết:
a) Ta có:
\(\begin{array}{l}OB//O'B'\\ = > OA//O'A',AB//A'B'\end{array}\)
Mà ta thấy điểm O và O’ , điểm A va A’, điểm B và B’ đều có tung độ cách nhau 2 đơn vị với hoành độ lần lượt là 0, 1, 2.
b) Ta có:
Với \(x = 0\) thì \(y = 3.0 = 0\) => đồ thị hàm số \(y = 3x\) đi qua O
Với \(x = 1\) thì \(y = 3.1 = 3\) => đồ thị hàm số \(y = 3x\) đi qua A
Với \(x = 2\) thì \(y = 3.2 = 6\) => đồ thì hàm số \(y = 3x\) đi qua
c) Ta có:
Với \(x = 0\) thì \(y = 3.0 - 2 = - 2\) => đồ thị hàm số \(y = 3x - 2\) đi qua O’
Với \(x = 1\) thì \(y = 3.1 - 2 = 1\) => đồ thị hàm số \(y = 3x - 2\) đi qua A’
Với \(x = 2\) thì \(y = 3.2 - 2 = 4\) => đồ thị hàm số \(y = 3x - 2\) đi qua B’
Vẽ đồ thị của các hàm số sau:
a) \(y = 3x + 1\)
b) \(y = - 2x + 3\)
Phương pháp giải:
Để vẽ đồ thị hàm số \(y = ax + b\left( {a \ne 0} \right)\), ta chỉ cần xác định hai điểm phân biệt thuộc đồ thị rồi vẽ đường thẳng đi qua hai điểm đó.
Lời giải chi tiết:
a) \(y = 3x + 1\)
Vẽ hệ trục tọa độ \(Oxy\).
Cho \(x = 0\) ta được \(y = 1\)
Cho \(y = 0\) ta được \(x = \frac{{ - 1}}{3}\)
Đồ thì của hàm số \(y = 3x + 1\) là đường thẳng đi qua hai điểm \(A\left( {0;1} \right),B\left( {\frac{{ - 1}}{3};0} \right)\)

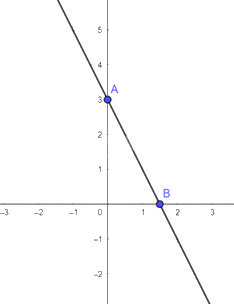
b) \(y = - 2x + 3\)
Vẽ hệ trục tọa độ \(Oxy\)
Cho \(x = 0\) ta được \(y = 3\)
Cho \(y = 0\) ta được \(x = \frac{3}{2}\)
Đồ thị của hàm số \(y = - 2x + 3\) là đường thẳng đi qua hai điểm \(A\left( {0;3} \right),B\left( {\frac{3}{2};0} \right)\)
Hãy trả lời câu hỏi trong phần Khởi động.
Các tác phẩm của danh hoạc Leonardo da Vinci không chỉ đặc sắc bởi tính nghệ thuật mà còn mang nhiều vẻ đẹp toán học. Khi vẽ người, ông quan tâm đến tỉ lệ chính xác của cơ thể nhằm tăng tính chân thức cho bức tranh. Ông đã vẽ bức tranh “Vitruvian Man” thể hiện ý tưởng về tỉ lệ hoàn mĩ của cơ thể người (Hình 5.19).
Trong bức tranh này, chiều cao của một người bằng tám lần chiều cao của đầu người đó (khoảng cách từ cằm đến đỉnh đầu). Đã từ lâu, đây là một quy chuẩn trong hội họa và sau này được nghiên cứu, phát triển ứng dụng trong kiến trúc
Từ bức tranh này, có thể biểu diễn mối quan hệ giữa chiều dài sải tay và chiều cao của một người như nào.
Phương pháp giải:
Dựa vào định nghĩa hàm số bậc nhất và mối quan hệ của chiều dài sải tay và chiều cao của một người để biểu diễn dưới dạng \(y = ax + b\)
Lời giải chi tiết:
Dựa vào bức tranh ta thấy chiều dài sải tay gấp ba lần chiều cao đầu của người đó. Gọi chiều dài sải tay là x thì chiều cao đầu người đó là \(\frac{1}{3}x\).
Mà chiều cao của một người bằng tám lần chiều cao của đầu người đó:
\(y = 8.\frac{1}{3}x = \frac{8}{3}x\)
Mục 2 của chương trình Toán 8 thường tập trung vào các kiến thức cơ bản về đa thức, các phép toán trên đa thức, và các ứng dụng của chúng. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Mục 2 thường bao gồm các nội dung sau:
Trang 14 thường chứa các bài tập vận dụng kiến thức về đa thức nhiều biến để thực hiện các phép toán đơn giản. Ví dụ:
Để giải các bài tập này, các em cần nắm vững định nghĩa về bậc của đa thức và quy tắc tính giá trị của đa thức.
Trang 15 thường chứa các bài tập phức tạp hơn, đòi hỏi các em phải vận dụng nhiều kiến thức và kỹ năng. Ví dụ:
Để giải các bài tập này, các em cần nắm vững quy tắc thu gọn đa thức và phương pháp tìm nghiệm của đa thức.
Trang 16 thường chứa các bài tập ứng dụng, yêu cầu các em phải giải các bài toán thực tế liên quan đến đa thức. Ví dụ:
Để giải các bài tập này, các em cần nắm vững công thức tính diện tích hình chữ nhật và hình vuông, và biết cách biểu diễn các đại lượng bằng đa thức.
Để học tốt Toán 8, các em cần:
Ngoài SGK Toán 8, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng với bài viết này, các em đã hiểu rõ hơn về cách giải các bài tập trong mục 2 trang 14, 15, 16 SGK Toán 8. Chúc các em học tốt và đạt kết quả cao trong môn Toán!
| Bài tập | Nội dung |
|---|---|
| Bài 1 (Trang 14) | Tìm bậc của đa thức |
| Bài 2 (Trang 14) | Tính giá trị của đa thức |
| Bài 3 (Trang 15) | Thu gọn đa thức |