Chào mừng bạn đến với bài học lý thuyết Cộng, trừ, nhân đa thức thuộc chương trình Toán 8. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về các phép toán này, giúp bạn tự tin giải các bài tập trong SGK và các bài kiểm tra.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, tính chất và các ví dụ minh họa để hiểu rõ hơn về cách thực hiện các phép toán cộng, trừ, nhân đa thức.
Cộng và trừ hai đa thức như thế nào?
1. Cộng và trừ hai đa thức
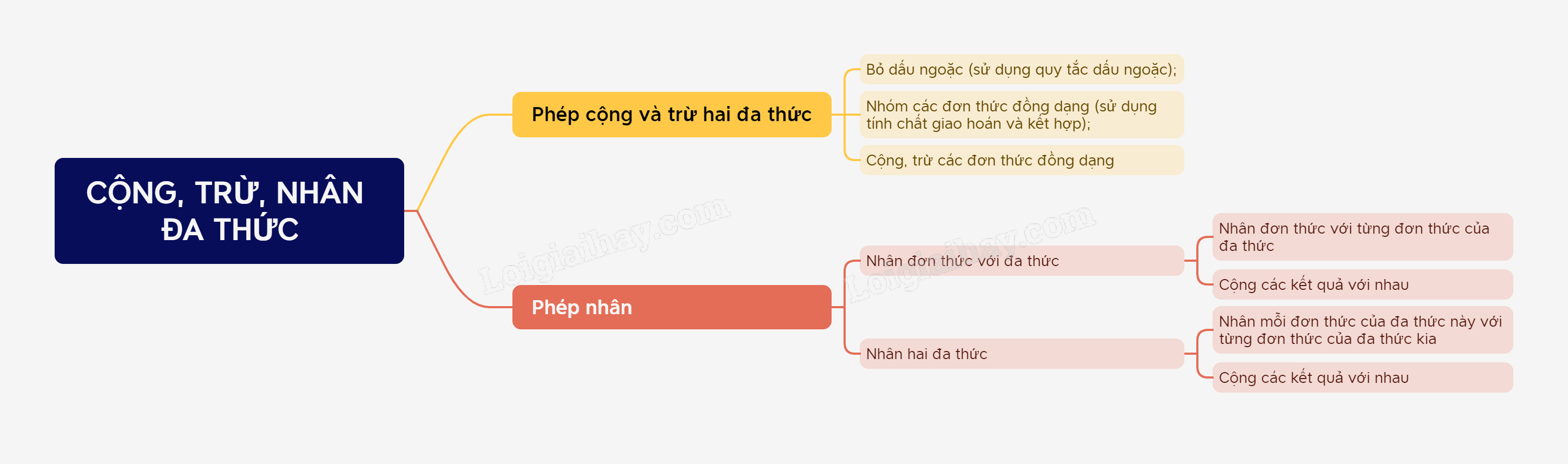
Để cộng, trừ hai đa thức ta thực hiện các bước:
- Bỏ dấu ngoặc (sử dụng quy tắc dấu ngoặc);
- Nhóm các đơn thức đồng dạng (sử dụng tính chất giao hoán và kết hợp);
- Cộng, trừ các đơn thức đồng dạng
Ví dụ:
Cho hai đa thức \(A = 3{x^2} - xy\) và \(B = {x^2} + 2xy - {y^2}\)
\(\begin{array}{l}A + B = \left( {3{x^2} - xy} \right) + \left( {{x^2} + 2xy - {y^2}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\, = 3{x^2} - xy + {x^2} + 2xy - {y^2}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = (3{x^2} + {x^2}) + ( - xy + 2xy) - {y^2}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = 4{x^2} + xy - {y^2}\end{array}\)
\(\begin{array}{l}A - B = \left( {3{x^2} - xy} \right) - \left( {{x^2} + 2xy - {y^2}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\, = 3{x^2} - xy - {x^2} - 2xy + {y^2}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = (3{x^2} - {x^2}) + ( - xy - 2xy) + {y^2}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = 2{x^2} - 3xy + {y^2}\end{array}\)
2. Nhân đơn thức với đa thức
Để nhân đơn thức với đa thức, ta nhân đơn thức đó với từng hạng tử của đa thức, rồi cộng các kết quả với nhau.
Ví dụ:
\(\begin{array}{l}3{x^2}y\left( {2{x^2}y - xy + 3{y^2}} \right)\\ = (3{x^2}y).(2{x^2}y) - (3{x^2}y).(xy) + (3{x^2}y).(3{y^2})\\ = 3.2.({x^2}.{x^2})\left( {y.y} \right) - 3.({x^2}.x).\left( {y.y} \right) + 3.3.{x^2}.\left( {y.{y^2}} \right)\\ = 6{x^4}{y^2} - 3{x^3}.{y^2} + 9{x^2}{y^3}\end{array}\)
3. Nhân hai đa thức
Để nhân hai đa thức, ta nhân từng hạng tử của đa thức này với đa thức kia, rồi cộng các kết quả với nhau.
Ví dụ:
\(\begin{array}{l}(xy + 1)(xy - 3)\\ = (xy).\left( {xy} \right) + xy - 3xy - 3\\ = {x^2}{y^2} - 2xy - 3\end{array}\)
Trong chương trình Toán 8, việc nắm vững lý thuyết về cộng, trừ, nhân đa thức là nền tảng quan trọng để giải quyết các bài toán đại số phức tạp hơn. Bài viết này sẽ trình bày chi tiết lý thuyết, ví dụ minh họa và các bài tập thực hành để giúp bạn hiểu rõ và áp dụng kiến thức một cách hiệu quả.
Cộng đa thức là phép toán kết hợp các đơn thức đồng dạng để tạo thành một đa thức mới. Để cộng hai đa thức, ta thực hiện các bước sau:
Ví dụ: Cộng hai đa thức A = 2x2 + 3x - 5 và B = -x2 + 5x + 2
A + B = (2x2 - x2) + (3x + 5x) + (-5 + 2) = x2 + 8x - 3
Trừ đa thức là phép toán tìm hiệu của hai đa thức. Để trừ hai đa thức, ta thực hiện các bước sau:
Ví dụ: Trừ đa thức B = -x2 + 5x + 2 khỏi đa thức A = 2x2 + 3x - 5
A - B = 2x2 + 3x - 5 - (-x2 + 5x + 2) = 2x2 + 3x - 5 + x2 - 5x - 2 = 3x2 - 2x - 7
Nhân đa thức là phép toán tìm tích của hai đa thức. Để nhân hai đa thức, ta thực hiện các bước sau:
Ví dụ: Nhân hai đa thức A = 2x + 3 và B = x - 1
A * B = (2x + 3)(x - 1) = 2x(x - 1) + 3(x - 1) = 2x2 - 2x + 3x - 3 = 2x2 + x - 3
Trong quá trình thực hiện các phép toán với đa thức, việc sử dụng các hằng đẳng thức đáng nhớ sẽ giúp bạn giải quyết bài toán nhanh chóng và hiệu quả hơn. Một số hằng đẳng thức thường gặp:
Để củng cố kiến thức, hãy thử giải các bài tập sau:
Lý thuyết về cộng, trừ, nhân đa thức là một phần quan trọng trong chương trình Toán 8. Việc nắm vững lý thuyết và thực hành thường xuyên sẽ giúp bạn tự tin giải quyết các bài toán đại số và xây dựng nền tảng vững chắc cho các kiến thức toán học nâng cao hơn.