Chào mừng các em học sinh đến với bài giải chi tiết bài 6.3 trang 42 SGK Toán 8. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả nhất.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em chinh phục môn Toán một cách tự tin.
Tính độ dài \(x\) trong mỗi trường hợp ở hình 6.15
Đề bài
Tính độ dài \(x\) trong mỗi trường hợp ở hình 6.15.
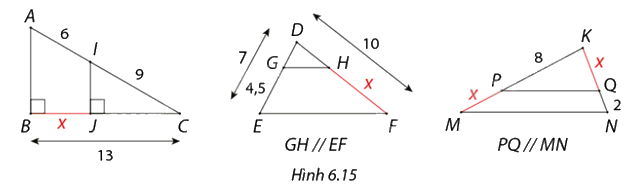
Phương pháp giải - Xem chi tiết
Dựa vào định lí Thales thuận để tìm độ dài x:
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết
Xét tam giác \(ABC\), ta có:
\(\begin{array}{l}\widehat {ABC} = 90^\circ \\\widehat {IJC} = 90^\circ \end{array}\)(mà hai góc này ở vị trí đồng vị)
=> \(IJ//AB\)
Dựa vào định lí Thales thuận ta có:
\(\begin{array}{l}\frac{{IA}}{{AC}} = \frac{6}{{15}}\\\frac{{JB}}{{BC}} = \frac{x}{{13}}\\\frac{{IA}}{{AC}} = \frac{{JB}}{{AC}} \Leftrightarrow \frac{6}{{15}} = \frac{x}{{13}} \Rightarrow x = 5,2\end{array}\)
Xét tam giác \(DEF\), ta có:
\(GH//EF\)
=> \(\frac{{GE}}{{DE}} = \frac{{HF}}{{DF}} \Leftrightarrow \frac{{4,5}}{7} = \frac{x}{{10}} \Rightarrow x = \frac{{45}}{7}\)
Xét tam giác \(KMN\), ta có:
\(PQ//MN\)
=> \(\frac{{PM}}{{PK}} = \frac{{QN}}{{QK}} \Leftrightarrow \frac{x}{8} = \frac{2}{x} \Leftrightarrow x = 4\)
Bài 6.3 trang 42 SGK Toán 8 thuộc chương trình đại số lớp 8, tập trung vào việc vận dụng các kiến thức về hình chữ nhật để giải quyết các bài toán thực tế. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về hình chữ nhật, bao gồm:
Bài tập 6.3 trang 42 SGK Toán 8 thường yêu cầu học sinh:
Để giải bài 6.3 trang 42 SGK Toán 8, học sinh cần thực hiện các bước sau:
Bài toán: Cho hình chữ nhật ABCD, có AB = 8cm, BC = 6cm. Tính độ dài đường chéo AC.
Giải:
Vì ABCD là hình chữ nhật nên góc ABC vuông. Do đó, tam giác ABC vuông tại B.
Áp dụng định lý Pitago vào tam giác ABC, ta có:
AC2 = AB2 + BC2
AC2 = 82 + 62 = 64 + 36 = 100
AC = √100 = 10cm
Vậy, độ dài đường chéo AC là 10cm.
Ngoài SGK Toán 8, học sinh có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức về hình chữ nhật:
Hy vọng với bài viết này, các em học sinh đã nắm vững kiến thức và phương pháp giải bài 6.3 trang 42 SGK Toán 8. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!