Chào mừng các em học sinh đến với bài giải chi tiết mục 1 trang 22, 23 sách giáo khoa Toán 8. Tại giaitoan.edu.vn, chúng tôi cung cấp các lời giải bài tập Toán 8 được trình bày rõ ràng, dễ hiểu, giúp các em tự tin hơn trong quá trình học tập.
Mục tiêu của chúng tôi là hỗ trợ các em học sinh nắm vững kiến thức Toán 8, đồng thời rèn luyện kỹ năng giải bài tập một cách hiệu quả. Hãy cùng chúng tôi khám phá và chinh phục những bài toán Toán 8 một cách dễ dàng nhất!
Trong Hình 5.32, mỗi quả cân có khối lượng x kg.
Xét xem \(x = - 2\) là nghiệm của phương trình nào trong các phương trình sau:
a) \(2x - 7 = 5x - 1\)
b) \(x\left( {x - 2} \right) = 6 - 2x\)
Phương pháp giải:
Giải một phương trình là tìm tất cả các nghiệm của phương trình đó. Để xét xem \(x = - 2\) là nghiệm của phương trình nào ta thay \(x = - 2\) vào vế trái và vế phải của các phương trình. Nếu giá trị của cả hai vế bằng nhau thì \(x = - 2\) chính là nghiệm của phương trình đó.
Lời giải chi tiết:
a) Lần lượt thay \(x = - 2\) vào vế trái và vế phải của phương trình \(2x - 7 = 5x - 1\), ta có:
Vế trái: \(2. - 2 - 7 = - 11\)
Vế phải: \(5. - 2 - 1 = - 11\)
Vậy \(x = - 2\) là nghiệm của phương trình \(2x - 7 = 5x - 1\).
b) Lần lượt thay \(x = - 2\) vào vế trái và vế phải của phương trình \(x\left( {x - 2} \right) = 6 - 2x\), ta có:
Vế trái: \( - 2\left( { - 2 - 2} \right) = 8\)
Vế phải: \(6 + \left( { - 2. - 2} \right) = 2\)
Vậy \(x = - 2\) không phải nghiệm của phương trình \(x\left( {x - 2} \right) = 6 - 2x\).
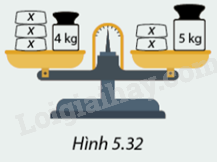
Trong Hình 5.32, mỗi quả cân có khối lượng x kg. Viết hệ thức liên hệ giữa khối lượng đồ vật trên hai đĩa cân khi thăng bằng.
Phương pháp giải:
Viết hệ thức liên hệ giữa khối lượng đồ vật trên hai đĩa cân khi cân bằng.
Lời giải chi tiết:
Hệ thức liên hệ giữa khối lượng đồ vật trên hai đĩa cân khi cân bằng là:
\(3x + 4 = 2x + 5\)
Xét xem \(x = - 2\) là nghiệm của phương trình nào trong các phương trình sau:
a) \(2x - 7 = 5x - 1\)
b) \(x\left( {x - 2} \right) = 6 - 2x\)
Phương pháp giải:
Giải một phương trình là tìm tất cả các nghiệm của phương trình đó. Để xét xem \(x = - 2\) là nghiệm của phương trình nào ta thay \(x = - 2\) vào vế trái và vế phải của các phương trình. Nếu giá trị của cả hai vế bằng nhau thì \(x = - 2\) chính là nghiệm của phương trình đó.
Lời giải chi tiết:
a) Lần lượt thay \(x = - 2\) vào vế trái và vế phải của phương trình \(2x - 7 = 5x - 1\), ta có:
Vế trái: \(2. - 2 - 7 = - 11\)
Vế phải: \(5. - 2 - 1 = - 11\)
Vậy \(x = - 2\) là nghiệm của phương trình \(2x - 7 = 5x - 1\).
b) Lần lượt thay \(x = - 2\) vào vế trái và vế phải của phương trình \(x\left( {x - 2} \right) = 6 - 2x\), ta có:
Vế trái: \( - 2\left( { - 2 - 2} \right) = 8\)
Vế phải: \(6 + \left( { - 2. - 2} \right) = 2\)
Vậy \(x = - 2\) không phải nghiệm của phương trình \(x\left( {x - 2} \right) = 6 - 2x\).
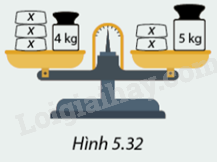
Trong Hình 5.32, mỗi quả cân có khối lượng x kg. Viết hệ thức liên hệ giữa khối lượng đồ vật trên hai đĩa cân khi thăng bằng.
Phương pháp giải:
Viết hệ thức liên hệ giữa khối lượng đồ vật trên hai đĩa cân khi cân bằng.
Lời giải chi tiết:
Hệ thức liên hệ giữa khối lượng đồ vật trên hai đĩa cân khi cân bằng là:
\(3x + 4 = 2x + 5\)
Mục 1 của chương trình Toán 8 thường tập trung vào việc ôn tập và mở rộng kiến thức về các phép toán cơ bản, các biểu thức đại số đơn giản, và các khái niệm về số thực. Việc nắm vững kiến thức nền tảng này là vô cùng quan trọng để học tốt các chương tiếp theo. Bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện tư duy logic và khả năng tính toán.
Để giúp các em học sinh hiểu rõ hơn về nội dung và phương pháp giải các bài tập trong mục 1 trang 22, 23 SGK Toán 8, chúng tôi sẽ phân tích chi tiết từng bài tập:
Bài tập này yêu cầu học sinh tính giá trị của các biểu thức đại số đơn giản. Để giải bài tập này, học sinh cần nắm vững các quy tắc về thứ tự thực hiện các phép toán, các tính chất của phép cộng, phép trừ, phép nhân, phép chia, và các quy tắc về dấu ngoặc.
Ví dụ:
Tính giá trị của biểu thức: 3x + 2y - 5z khi x = 2, y = -1, z = 3
Giải:
3x + 2y - 5z = 3(2) + 2(-1) - 5(3) = 6 - 2 - 15 = -11
Bài tập này yêu cầu học sinh rút gọn các biểu thức đại số phức tạp hơn. Để giải bài tập này, học sinh cần nắm vững các quy tắc về phép nhân, phép chia đa thức, các hằng đẳng thức đại số, và các kỹ năng biến đổi biểu thức.
Ví dụ:
Rút gọn biểu thức: (x + 2)(x - 2) + x2
Giải:
(x + 2)(x - 2) + x2 = x2 - 4 + x2 = 2x2 - 4
Bài tập này yêu cầu học sinh giải các phương trình bậc nhất một ẩn. Để giải bài tập này, học sinh cần nắm vững các quy tắc về phép biến đổi tương đương phương trình, các kỹ năng giải phương trình, và các điều kiện xác định của phương trình.
Ví dụ:
Giải phương trình: 2x + 3 = 7
Giải:
2x + 3 = 7
2x = 7 - 3
2x = 4
x = 2
Để giải bài tập Toán 8 một cách hiệu quả, học sinh cần:
Kiến thức trong mục 1 có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống, như:
Hãy dành thời gian ôn tập và làm bài tập thường xuyên để nắm vững kiến thức Toán 8. Đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè nếu gặp khó khăn. Chúc các em học tập tốt!