Chào mừng các em học sinh đến với bài giải chi tiết mục 3 trang 82, 83 sách giáo khoa Toán 8. Tại giaitoan.edu.vn, chúng tôi cung cấp các lời giải bài tập Toán 8 chính xác, dễ hiểu, giúp các em học tập hiệu quả.
Mục tiêu của chúng tôi là hỗ trợ các em học sinh tự học, củng cố kiến thức và đạt kết quả tốt nhất trong môn Toán.
1. Từ dấu hiệu nhận biết hình thoi, em hãy bổ sung thêm một điều kiện để một hình chữ nhật là hình vuông.
1. Từ dấu hiệu nhận biết hình thoi, em hãy bổ sung thêm một điều kiện để một hình chữ nhật là hình vuông.
2. Từ dấu hiệu nhận biết hình chữ nhật, em hãy bổ sung một điều kiện để một hình thoi là hình vuông.
Phương pháp giải:
Dựa vào dấu hiệu nhận biết hình thoi, bổ sung thêm điều kiện để hình chữ nhật là hình vuông.
Dựa vào dấu hiệu nhận biết hình chữ nhật, bổ sung thêm điều kiện để hình thoi là hình vuông.
Lời giải chi tiết:
1. Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông;
Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
2. Hình thoi có 1 góc vuông là hình vuông
Hình thoi có hai đường chéo bằng nhau là hình vuông.
Một mặt bánh chưng có dạng hình vuông ABCD được cắt theo bốn đường thẳng \(AC,BD,MP,NQ\) trong đó \(M,N,P,Q\) lần lượt là trung điểm các cạnh \(AB,BC,CD,AD\)(hình 3.81). Vì sao bốn đường cắt này đồng quy?
Phương pháp giải:
Dựa vào tính chất của hình vuông và hình bình hành để chứng minh.
Lời giải chi tiết:
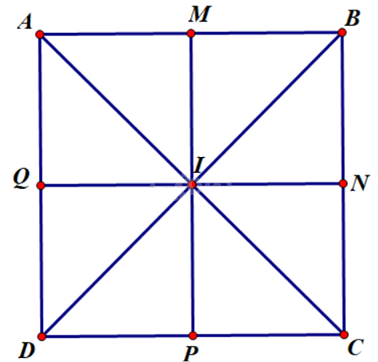
Gọi I là trung điểm của AC suy ra AC và BD cắt nhau tại I (ABCD là hình vuông). (1)
Xét tứ giác AMCP có \(AM//CP\left( {AB//CD} \right)\) và \(AM = CP\left( { = \frac{1}{2}AB = \frac{1}{2}CD} \right)\)
Suy ra tứ giác AMCP là hình bình hành\( \Rightarrow \) AC và MP cắt nhau tại I (2)
Xét tứ giác AQCN có \(AQ//NC\left( {AD//BC} \right)\) và \(AQ = NC\left( { = \frac{1}{2}AD = \frac{1}{2}CB} \right)\)
Suy ra tứ giác AQCN là hình bình hành\( \Rightarrow \) AC và QN cắt nhau tại I (3)
Từ (1); (2) và (3) suy ra \(AC,BD,MP,NQ\) đồng quy tại I.
1. Từ dấu hiệu nhận biết hình thoi, em hãy bổ sung thêm một điều kiện để một hình chữ nhật là hình vuông.
2. Từ dấu hiệu nhận biết hình chữ nhật, em hãy bổ sung một điều kiện để một hình thoi là hình vuông.
Phương pháp giải:
Dựa vào dấu hiệu nhận biết hình thoi, bổ sung thêm điều kiện để hình chữ nhật là hình vuông.
Dựa vào dấu hiệu nhận biết hình chữ nhật, bổ sung thêm điều kiện để hình thoi là hình vuông.
Lời giải chi tiết:
1. Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông;
Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
2. Hình thoi có 1 góc vuông là hình vuông
Hình thoi có hai đường chéo bằng nhau là hình vuông.
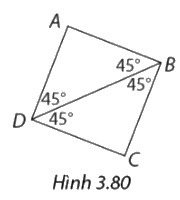
Tứ giác ABCD trong hình 3.80 có là hình vuông không? Vì sao?
Phương pháp giải:
Dựa vào dấu hiệu nhận biết hình vuông để xác định.
Lời giải chi tiết:
Xét tứ giác ABCD có \(AB//CD;AD//BC\) (có 1 cặp góc so le trong bằng nhau)
Suy ra ABCD là hình bình hành.
Có \(\widehat B = 45^\circ + 45^\circ = 90^\circ \) suy ra ABCD là hình chữ nhật (1)
Xét tam giác ABD có \(\widehat B = \widehat D = 45^\circ \) nên tam giác ABD cân tại A
\( \Rightarrow AD = AB\left( 2 \right)\)
Từ (1) và (2) suy ra tứ giác ABCD là hình vuông.
Một mặt bánh chưng có dạng hình vuông ABCD được cắt theo bốn đường thẳng \(AC,BD,MP,NQ\) trong đó \(M,N,P,Q\) lần lượt là trung điểm các cạnh \(AB,BC,CD,AD\)(hình 3.81). Vì sao bốn đường cắt này đồng quy?
Phương pháp giải:
Dựa vào tính chất của hình vuông và hình bình hành để chứng minh.
Lời giải chi tiết:
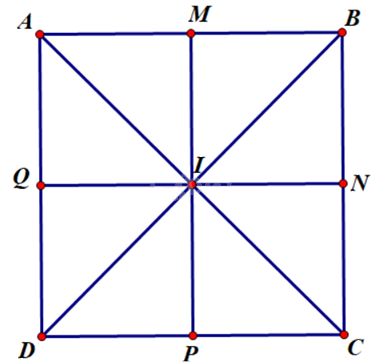
Gọi I là trung điểm của AC suy ra AC và BD cắt nhau tại I (ABCD là hình vuông). (1)
Xét tứ giác AMCP có \(AM//CP\left( {AB//CD} \right)\) và \(AM = CP\left( { = \frac{1}{2}AB = \frac{1}{2}CD} \right)\)
Suy ra tứ giác AMCP là hình bình hành\( \Rightarrow \) AC và MP cắt nhau tại I (2)
Xét tứ giác AQCN có \(AQ//NC\left( {AD//BC} \right)\) và \(AQ = NC\left( { = \frac{1}{2}AD = \frac{1}{2}CB} \right)\)
Suy ra tứ giác AQCN là hình bình hành\( \Rightarrow \) AC và QN cắt nhau tại I (3)
Từ (1); (2) và (3) suy ra \(AC,BD,MP,NQ\) đồng quy tại I.
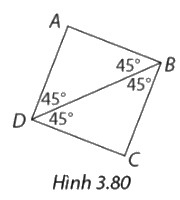
Tứ giác ABCD trong hình 3.80 có là hình vuông không? Vì sao?
Phương pháp giải:
Dựa vào dấu hiệu nhận biết hình vuông để xác định.
Lời giải chi tiết:
Xét tứ giác ABCD có \(AB//CD;AD//BC\) (có 1 cặp góc so le trong bằng nhau)
Suy ra ABCD là hình bình hành.
Có \(\widehat B = 45^\circ + 45^\circ = 90^\circ \) suy ra ABCD là hình chữ nhật (1)
Xét tam giác ABD có \(\widehat B = \widehat D = 45^\circ \) nên tam giác ABD cân tại A
\( \Rightarrow AD = AB\left( 2 \right)\)
Từ (1) và (2) suy ra tứ giác ABCD là hình vuông.
Mục 3 trong sách giáo khoa Toán 8 trang 82 và 83 thường tập trung vào một chủ đề cụ thể, ví dụ như các định lý liên quan đến hình bình hành, hình chữ nhật, hình thoi, hình vuông, hoặc các bài toán ứng dụng về các tứ giác đặc biệt này. Việc nắm vững kiến thức nền tảng và phương pháp giải là vô cùng quan trọng để giải quyết các bài tập một cách hiệu quả.
Thông thường, mục này sẽ bao gồm:
Để giải tốt các bài tập trong mục này, học sinh cần:
Bài tập: Cho hình chữ nhật ABCD, O là giao điểm của hai đường chéo. Chứng minh rằng OA = OB = OC = OD.
Giải:
Vì ABCD là hình chữ nhật nên hai đường chéo AC và BD bằng nhau và cắt nhau tại trung điểm O của mỗi đường. Do đó, OA = OC = AC/2 và OB = OD = BD/2. Mà AC = BD (tính chất hình chữ nhật) nên OA = OC = OB = OD.
Các bài tập thường gặp bao gồm:
Học sinh cần lưu ý:
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau:
Việc giải bài tập Mục 3 trang 82, 83 SGK Toán 8 đòi hỏi học sinh phải nắm vững kiến thức nền tảng, phương pháp giải và luyện tập thường xuyên. Hy vọng với những hướng dẫn và ví dụ minh họa trên, các em học sinh sẽ tự tin hơn trong việc giải các bài tập Toán 8 và đạt kết quả tốt nhất.