Chào mừng bạn đến với bài học lý thuyết về những hằng đẳng thức đáng nhớ trong chương trình Toán 8. Đây là một phần kiến thức nền tảng vô cùng quan trọng, giúp bạn giải quyết nhiều bài toán đại số một cách nhanh chóng và hiệu quả.
Tại giaitoan.edu.vn, chúng tôi cung cấp tài liệu học tập đầy đủ, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Hằng đẳng thức là gì?
1. Hằng đẳng thức
Cho hai biểu thức đại số A và B có cùng các biến. Nếu giá trị của A và giá trị của B luôn bằng nhau tại mọi giá trị của các biến thì ta có một hằng đẳng thức A = B(hay đồng nhất thức)
Ví dụ: \(a + b = b + a;a(a + 2) = {a^2} + 2a\) là những hằng đẳng thức.
\({a^2} - 1 = 3a;a(a - 1) = 2a\) không phải là những hằng đẳng thức.
2. Những hằng đẳng thức đáng nhớ
+ Bình phương của một tổng
\({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\)
Ví dụ: \({101^2} = {(100 + 1)^2} = {100^2} + 2.100.1 + {1^2} = 10201\)
+ Bình phương của một hiệu
\({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\)
Ví dụ: \({99^2} = {(100 - 1)^2} = {100^2} - 2.100.1 + {1^2} = 9801\)
+ Hiệu hai bình phương
\({A^2} - {B^2} = (A - B)(A + B)\)
Ví dụ: \({101^2} - {99^2} = (101 - 99)(101 + 99) = 2.200 = 400\)
+ Lập phương của một tổng
\({\left( {A + B} \right)^3} = {A^3} + 3{A^2}B + 3A{B^2} + {B^3}\)
Ví dụ: \({\left( {x + 3} \right)^3} = {x^3} + 3{x^2}.3 + 3x{.3^2} + {3^3} = {x^3} + 9{x^2} + 27x + 27\)
+ Lập phương của một hiệu
\({\left( {A - B} \right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}\)
Ví dụ: \({\left( {x - 3} \right)^3} = {x^3} - 3{x^2}.3 + 3x{.3^2} - {3^3} = {x^3} - 9{x^2} + 27x - 27\)
+ Tổng hai lập phương
\({A^3} + {B^3} = (A + B)\left( {{A^2} - AB + {B^2}} \right)\)
Ví dụ: \({x^3} + 8 = {x^3} + {2^3} = (x + 2)({x^2} - 2x + 4)\)
+ Hiệu hai lập phương
\({A^3} - {B^3} = (A - B)\left( {{A^2} + AB + {B^2}} \right)\)
Ví dụ: \({x^3} - 8 = \left( {x - 2} \right)\left( {{x^2} + 2x + 4} \right)\)
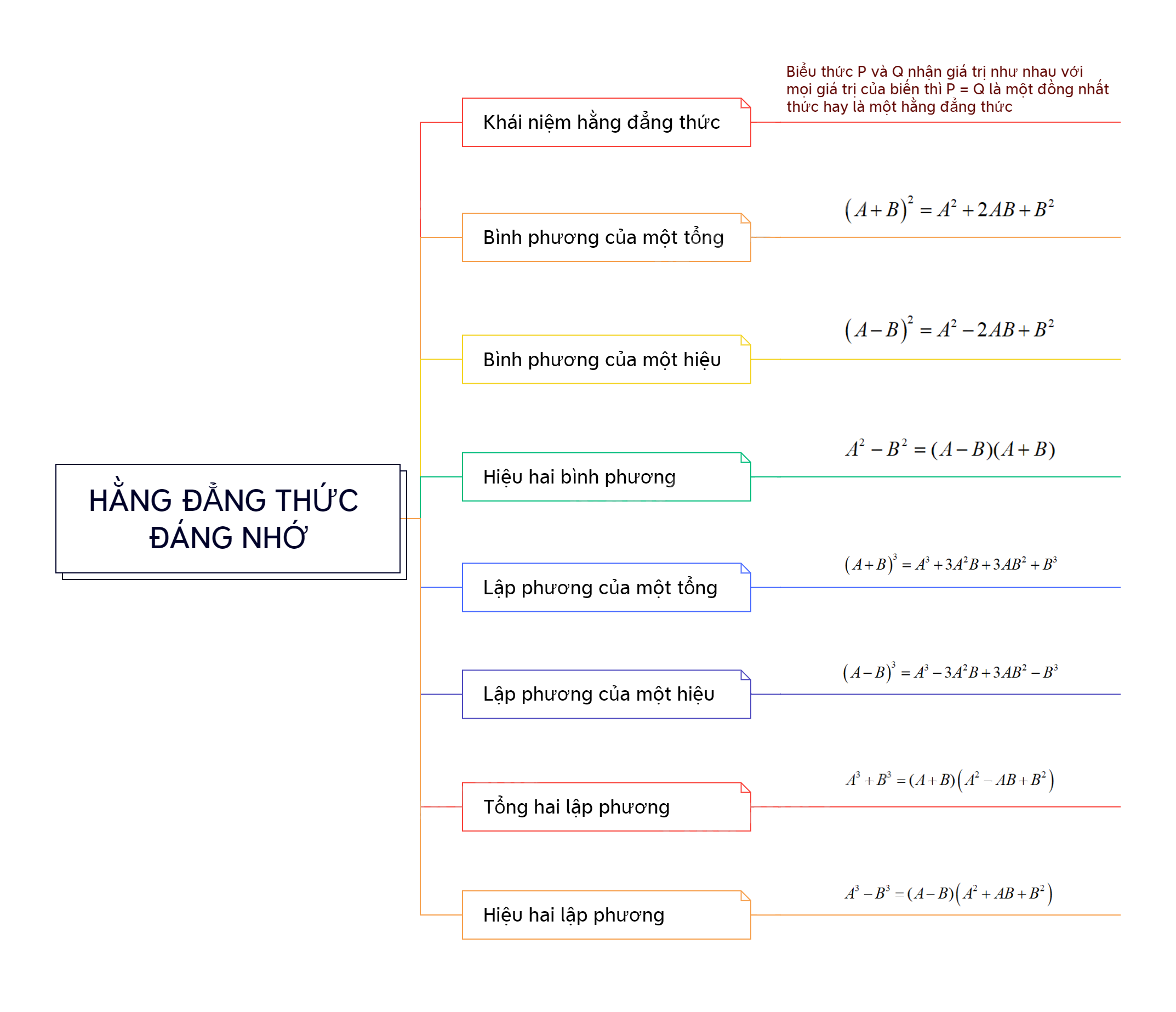
Những hằng đẳng thức đáng nhớ là những biểu thức đại số luôn đúng với mọi giá trị của biến. Việc nắm vững các hằng đẳng thức này không chỉ giúp bạn giải toán nhanh hơn mà còn là nền tảng cho các kiến thức toán học nâng cao hơn.
(a + b)² = a² + 2ab + b²
Hằng đẳng thức này cho biết bình phương của một tổng hai số bằng tổng của bình phương hai số đó cộng với hai lần tích của hai số.
(a - b)² = a² - 2ab + b²
Hằng đẳng thức này cho biết bình phương của một hiệu hai số bằng tổng của bình phương hai số đó trừ đi hai lần tích của hai số.
(a + b)(a - b) = a² - b²
Hằng đẳng thức này cho biết tích của một tổng và một hiệu hai số bằng hiệu của bình phương hai số đó.
(a + b)³ = a³ + 3a²b + 3ab² + b³
Hằng đẳng thức này cho biết lập phương của một tổng hai số bằng tổng của lập phương hai số đó cộng với ba lần tích của bình phương số thứ nhất và số thứ hai, cộng với ba lần tích của số thứ nhất và bình phương số thứ hai.
(a - b)³ = a³ - 3a²b + 3ab² - b³
Hằng đẳng thức này cho biết lập phương của một hiệu hai số bằng tổng của lập phương hai số đó trừ đi ba lần tích của bình phương số thứ nhất và số thứ hai, cộng với ba lần tích của số thứ nhất và bình phương số thứ hai.
a³ + b³ = (a + b)(a² - ab + b²)
Hằng đẳng thức này cho biết tổng hai lập phương bằng tích của tổng hai số và hiệu bình phương của hai số đó.
a³ - b³ = (a - b)(a² + ab + b²)
Hằng đẳng thức này cho biết hiệu hai lập phương bằng tích của hiệu hai số và tổng bình phương của hai số đó.
Những hằng đẳng thức đáng nhớ được ứng dụng rộng rãi trong việc:
Để hiểu rõ hơn về những hằng đẳng thức đáng nhớ, chúng ta hãy cùng giải một số bài tập sau:
Lời khuyên: Hãy luyện tập thường xuyên để nắm vững các hằng đẳng thức và ứng dụng chúng một cách linh hoạt trong các bài toán khác nhau.
Ví dụ 1: Rút gọn biểu thức (x + 3)²
Áp dụng hằng đẳng thức (a + b)² = a² + 2ab + b², ta có:
(x + 3)² = x² + 2 * x * 3 + 3² = x² + 6x + 9
Ví dụ 2: Phân tích đa thức x² - 9 thành nhân tử
Áp dụng hằng đẳng thức a² - b² = (a + b)(a - b), ta có:
x² - 9 = x² - 3² = (x + 3)(x - 3)
Ví dụ 3: Tính giá trị của biểu thức 27³ + 1³
Áp dụng hằng đẳng thức a³ + b³ = (a + b)(a² - ab + b²), ta có:
27³ + 1³ = (27 + 1)(27² - 27 * 1 + 1²) = 28 * (729 - 27 + 1) = 28 * 703 = 19684
Những hằng đẳng thức đáng nhớ là công cụ vô cùng hữu ích trong quá trình học tập môn Toán. Hãy dành thời gian để học thuộc và hiểu rõ các hằng đẳng thức này, đồng thời luyện tập thường xuyên để nâng cao kỹ năng giải toán của bạn. Chúc bạn học tập tốt!