Chào mừng các em học sinh đến với bài giải chi tiết bài 3.30 trang 80 SGK Toán 8. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả nhất.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
Hàng rào được đóng từ các thanh gỗ thẳng như trong Hình 3.75 với các thanh
Đề bài
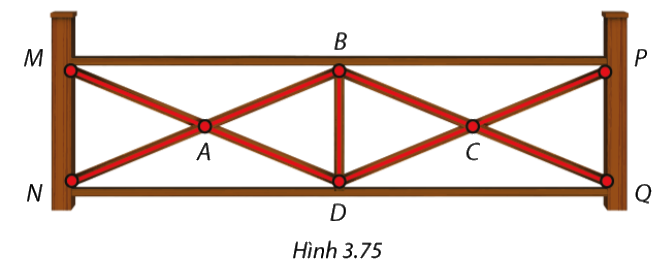
Hàng rào được đóng từ các thanh gỗ thẳng như trong Hình 3.75 với các thanh \(BN,BQ,DM,DP\) đều bằng 1,3 cm và thanh \(BD\) dài 0,5 cm. Điểm A là trung điểm chung của hai thành \(BN\)và \(DM\), điểm \(C\) là trung điểm chung của hai thanh \(BQ\) và \(DP\).
a) Chứng minh rằng tứ giác \(ABCD\) là hình thoi.
b) Tính khoảng cách giữa hai điểm A và C.
Phương pháp giải - Xem chi tiết
Dựa vào tính chất hai tam giác bằng nhau để chứng minh \(ABCD\) là hình thoi.
Sau đó tính khoảng cách giữa hai điểm A và C.
Lời giải chi tiết
a) Ta có:
Điểm A là trung điểm chung của hai thành \(BN\)và \(DM\)
Mà \(BN = DM\)
→ \(AB = AD\)
Điểm \(C\) là trung điểm chung của hai thanh \(BQ\) và \(DP\)
Mà \(BQ = DP\)
→ \(BC = CD\)
Mà \(BN = BQ = MD = DP\)
→ \(AB = AD = CB = CD\)
→ Tứ giác \(ABCD\) là hình thoi
b) Xét hình thoi \(ABCD\), ta có:
\(AB = AD = CB = CD = \frac{{1,3}}{2} = 0,65m\)
\(BD = 0,5m\)
\(AC = \sqrt {0,{{65}^2} - {{\left( {\frac{{0,5}}{2}} \right)}^2}} .2 = 1,2m\)
Vậy khoảng cách từ \(A\) đến \(C\) là \(1,2m\)
Bài 3.30 trang 80 SGK Toán 8 thuộc chương trình đại số lớp 8, tập trung vào việc vận dụng các kiến thức về hình chữ nhật để giải quyết các bài toán thực tế. Để giải bài này, học sinh cần nắm vững các tính chất của hình chữ nhật, đặc biệt là tính chất về các cạnh đối song song và bằng nhau, các góc vuông, và đường chéo bằng nhau.
Đề bài yêu cầu chúng ta chứng minh một tính chất liên quan đến hình chữ nhật. Cụ thể, đề bài thường đưa ra một hình chữ nhật ABCD và yêu cầu chứng minh một đẳng thức hoặc một mối quan hệ giữa các đoạn thẳng hoặc góc trong hình.
Để giải bài 3.30 trang 80 SGK Toán 8, học sinh có thể áp dụng các phương pháp sau:
(Ở đây sẽ là lời giải chi tiết của bài 3.30, bao gồm các bước chứng minh, giải thích rõ ràng và dễ hiểu. Ví dụ:)
Bài giải:
Xét hình chữ nhật ABCD, ta có:
Từ các tính chất trên, ta có thể chứng minh các đẳng thức hoặc mối quan hệ trong đề bài bằng cách sử dụng các phép biến đổi hình học và các phép toán số học.
Giả sử đề bài yêu cầu chứng minh rằng nếu E là giao điểm của hai đường chéo AC và BD, thì EA = EB = EC = ED. Ta có thể giải như sau:
Vì ABCD là hình chữ nhật nên AC = BD (tính chất hình chữ nhật). Do đó, AE = EC = BE = ED (tính chất đường trung tuyến của tam giác vuông). Vậy EA = EB = EC = ED.
Để củng cố kiến thức về bài 3.30 trang 80 SGK Toán 8, các em có thể làm thêm các bài tập tương tự sau:
Khi giải bài tập về hình chữ nhật, các em cần lưu ý những điều sau:
Bài 3.30 trang 80 SGK Toán 8 là một bài tập quan trọng giúp các em hiểu sâu hơn về hình chữ nhật và các tính chất của nó. Hy vọng rằng với bài giải chi tiết và các phương pháp giải được trình bày trong bài viết này, các em sẽ tự tin hơn khi giải các bài tập tương tự.