Lý thuyết Mặt phẳng tọa độ SGK Toán 8 - Cùng khám phá

Lý thuyết Mặt phẳng tọa độ - Nền tảng Toán học 8

Chào mừng bạn đến với bài học về Lý thuyết Mặt phẳng tọa độ trong chương trình Toán 8. Đây là một trong những kiến thức cơ bản và quan trọng, đặt nền móng cho các chương trình Toán học nâng cao hơn. Bài học này sẽ giúp bạn hiểu rõ về hệ tọa độ, cách xác định vị trí điểm trên mặt phẳng và ứng dụng của nó trong giải toán.

Giaitoan.edu.vn tự hào mang đến cho bạn một phương pháp học tập hiệu quả, với bài giảng được trình bày một cách dễ hiểu, kèm theo nhiều bài tập thực hành để bạn có thể rèn luyện và củng cố kiến thức.

Mặt phẳng tọa độ là gì?

1. Mặt phẳng tọa độ

Mặt phẳng có hệ trục tọa độ Oxy gọi là mặt phẳng tọa độ Oxy.

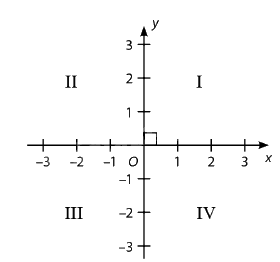
Lý thuyết Mặt phẳng tọa độ SGK Toán 8 - Cùng khám phá 1

Ox nằm ngang gọi là trục hoành;
Oy thẳng đứng gọi là trục tung;
O gọi là gốc tọa độ.

Hai trục tọa độ Ox, Oy chia mặt phẳng tọa độ Oxy thành bốn góc: góc phần tư thứ I, II, III, IV theo thứ tự ngược chiều kim đồng hồ.

Các đơn vị dài trên hai trục tọa độ được chọn bằng nhau (nếu không nói gì thêm).

2. Tọa độ của một điểm trên mặt phẳng tọa độ

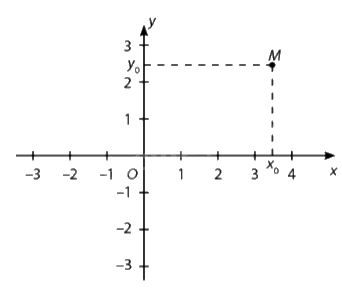
Trong mặt phẳng tọa độ, mỗi điểm M xác định duy nhất một cặp số (\({x_0};{y_0}\)) và ngược lại.

Cặp số (\({x_0};{y_0}\)) gọi là tọa độ của M, kí hiệu là M(\({x_0};{y_0}\)), trong đó \({x_0}\) là hoành độ, \({y_0}\) là tung độ của điểm M.

Mọi điểm thuộc trục hoành có tung độ bằng 0, Mọi điểm thuộc trục tung có hoành độ bằng 0.

Lý thuyết Mặt phẳng tọa độ SGK Toán 8 - Cùng khám phá 2

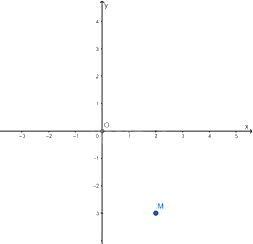
Ví dụ: Điểm M có tọa độ là (2; -3), kí hiệu là M(2; -3). Số 2 gọi là hoành độ, số -3 gọi là tung độ của điểm M.

Lý thuyết Mặt phẳng tọa độ SGK Toán 8 - Cùng khám phá 3

Lý thuyết Mặt phẳng tọa độ SGK Toán 8 - Cùng khám phá 4

Vững vàng kiến thức, bứt phá điểm số Toán 8! Đừng bỏ lỡ Lý thuyết Mặt phẳng tọa độ SGK Toán 8 - Cùng khám phá đặc sắc thuộc chuyên mục sgk toán 8 trên soạn toán. Với bộ bài tập toán trung học cơ sở được biên soạn chuyên sâu, bám sát từng chi tiết chương trình sách giáo khoa, con bạn sẽ củng cố kiến thức nền tảng vững chắc và dễ dàng chinh phục các dạng bài khó. Phương pháp học trực quan, logic sẽ giúp các em tối ưu hóa quá trình ôn luyện và đạt hiệu quả học tập tối đa!

Lý thuyết Mặt phẳng tọa độ SGK Toán 8 - Tổng quan

Mặt phẳng tọa độ là một công cụ quan trọng trong hình học, cho phép chúng ta biểu diễn vị trí của các điểm bằng các cặp số. Trong chương trình Toán 8, học sinh bắt đầu làm quen với khái niệm này và các ứng dụng cơ bản của nó.

1. Hệ tọa độ Descartes

Hệ tọa độ Descartes (hay còn gọi là hệ tọa độ vuông góc) bao gồm hai trục vuông góc nhau, gọi là trục hoành (Ox) và trục tung (Oy). Giao điểm của hai trục này là gốc tọa độ (O). Mỗi điểm trên mặt phẳng được xác định bởi một cặp số (x, y), gọi là tọa độ của điểm đó. x là hoành độ, y là tung độ.

2. Tọa độ của điểm

Để xác định tọa độ của một điểm trên mặt phẳng tọa độ, ta thực hiện các bước sau:

Từ điểm đó, kẻ đường vuông góc với trục Ox, giao điểm của đường này với trục Ox là điểm A. Hoành độ của điểm là khoảng cách từ O đến A (có dấu).
Từ điểm đó, kẻ đường vuông góc với trục Oy, giao điểm của đường này với trục Oy là điểm B. Tung độ của điểm là khoảng cách từ O đến B (có dấu).
Tọa độ của điểm là cặp số (hoành độ, tung độ).

3. Các trục tọa độ

Trục hoành (Ox): Là đường thẳng nằm ngang, là đường thẳng chứa gốc tọa độ và song song với trục x.
Trục tung (Oy): Là đường thẳng thẳng đứng, là đường thẳng chứa gốc tọa độ và song song với trục y.

4. Các phần của mặt phẳng tọa độ

Mặt phẳng tọa độ được chia thành bốn phần, gọi là các phần tư. Các phần tư được đánh số theo chiều ngược kim đồng hồ, bắt đầu từ phần tư thứ nhất (nằm ở góc phần tư trên bên phải).

Phần tư thứ nhất: x > 0, y > 0
Phần tư thứ hai: x < 0, y > 0
Phần tư thứ ba: x < 0, y < 0
Phần tư thứ tư: x > 0, y < 0

5. Ứng dụng của Mặt phẳng tọa độ

Mặt phẳng tọa độ có nhiều ứng dụng trong thực tế, bao gồm:

Biểu diễn vị trí của các đối tượng trên bản đồ.
Vẽ đồ thị của các hàm số.
Giải các bài toán hình học.

6. Bài tập ví dụ

Bài 1: Xác định tọa độ của các điểm A(2, 3), B(-1, 4), C(-2, -3), D(3, -1) trên mặt phẳng tọa độ.

Bài 2: Điểm nào sau đây nằm trong phần tư thứ hai? A(1, 2), B(-1, 2), C(-1, -2), D(1, -2)

7. Mở rộng kiến thức

Ngoài những kiến thức cơ bản trên, bạn có thể tìm hiểu thêm về:

Đường thẳng trên mặt phẳng tọa độ: Cách xác định phương trình đường thẳng và vẽ đồ thị của nó.
Hàm số bậc nhất: Mối liên hệ giữa hàm số bậc nhất và đường thẳng trên mặt phẳng tọa độ.

8. Luyện tập và củng cố

Để nắm vững kiến thức về Lý thuyết Mặt phẳng tọa độ, bạn nên luyện tập thường xuyên với các bài tập khác nhau. Giaitoan.edu.vn cung cấp một hệ thống bài tập phong phú, đa dạng, giúp bạn rèn luyện kỹ năng và củng cố kiến thức một cách hiệu quả.

9. Kết luận

Lý thuyết Mặt phẳng tọa độ là một kiến thức quan trọng trong chương trình Toán 8. Việc nắm vững kiến thức này sẽ giúp bạn giải quyết các bài toán hình học một cách dễ dàng và hiệu quả hơn. Chúc bạn học tập tốt!