Bài viết này cung cấp lý thuyết đầy đủ và chi tiết về trường hợp đồng dạng cạnh – góc – cạnh của tam giác, được trình bày theo chương trình SGK Toán 8. Chúng tôi sẽ giúp bạn hiểu rõ các điều kiện cần và đủ để hai tam giác đồng dạng, cùng với các ví dụ minh họa cụ thể.
Tại giaitoan.edu.vn, bạn không chỉ được học lý thuyết mà còn có cơ hội luyện tập với nhiều bài tập đa dạng, giúp củng cố kiến thức và nâng cao kỹ năng giải toán.
Trường hợp đồng dạng cạnh – góc – cạnh là gì?
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.
\(\begin{array}{l}\Delta ABC,\Delta A'B'C',\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}},\widehat {A'} = \widehat A\\ \Rightarrow \Delta A'B'C' \backsim \Delta ABC\,(c.g.c)\end{array}\)
Nhận xét: Tỉ số hai đường trung tuyến tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng.
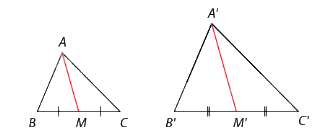
Nếu \(\Delta A'B'C' \backsim \Delta ABC\) với tỉ số đồng dạng k thì \(\frac{{A'M'}}{{AM}} = k\).
Trong chương trình Toán 8, việc nắm vững các trường hợp đồng dạng tam giác là vô cùng quan trọng. Một trong những trường hợp cơ bản và thường xuyên được sử dụng là trường hợp đồng dạng cạnh – góc – cạnh. Bài viết này sẽ đi sâu vào lý thuyết này, cung cấp các định nghĩa, điều kiện, và ví dụ minh họa để giúp bạn hiểu rõ hơn.
Hai tam giác được gọi là đồng dạng nếu chúng có ba góc bằng nhau và ba cạnh tương ứng tỉ lệ. Kí hiệu: △ABC ~ △A'B'C'.
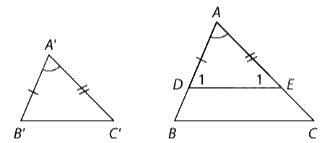
Phát biểu: Nếu hai tam giác có hai cạnh tương ứng tỉ lệ và góc xen giữa hai cạnh đó bằng nhau thì hai tam giác đó đồng dạng.
Kí hiệu: Nếu △ABC và △A'B'C' có:
Thì △ABC ~ △A'B'C'.
Chứng minh trường hợp đồng dạng cạnh – góc – cạnh dựa trên việc xây dựng một tam giác đồng dạng với tam giác đã cho. Quá trình chứng minh thường bao gồm việc sử dụng các tính chất của tam giác, các định lý về góc và cạnh, và các phép biến hình.
Ví dụ 1: Cho △ABC và △A'B'C' có AB = 6cm, AC = 8cm, A'B' = 9cm, A'C' = 12cm và ∠A = 70°. Chứng minh rằng △ABC ~ △A'B'C'.
Giải:
Ví dụ 2: Cho hình vẽ, biết AB = 4cm, AD = 6cm, AC = 8cm, AE = 12cm và ∠A chung. Chứng minh △ADE ~ △ABC.
(Hình vẽ minh họa với các điểm A, B, C, D, E được bố trí sao cho tạo thành hai tam giác có chung đỉnh A)
Giải:
Trường hợp đồng dạng cạnh – góc – cạnh được ứng dụng rộng rãi trong việc giải các bài toán liên quan đến tam giác đồng dạng, đặc biệt là trong các bài toán chứng minh hai tam giác đồng dạng để suy ra các tỉ lệ cạnh tương ứng và các góc bằng nhau.
Để củng cố kiến thức về trường hợp đồng dạng cạnh – góc – cạnh, bạn có thể thực hành với các bài tập sau:
Trường hợp đồng dạng cạnh – góc – cạnh là một công cụ quan trọng trong việc giải các bài toán hình học liên quan đến tam giác đồng dạng. Việc nắm vững lý thuyết và luyện tập thường xuyên sẽ giúp bạn tự tin hơn trong việc giải quyết các bài toán phức tạp.