Chào mừng các em học sinh đến với bài giải chi tiết bài 5.29 trang 30 SGK Toán 8. Bài tập này thuộc chương trình Toán 8 tập 1, nhằm giúp các em củng cố kiến thức về các phép biến đổi đại số và ứng dụng vào giải quyết bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi luôn cố gắng cung cấp những lời giải chính xác, dễ hiểu và phù hợp với trình độ của học sinh. Hãy cùng theo dõi bài giải dưới đây để nắm vững phương pháp và tự tin hơn trong quá trình học tập.
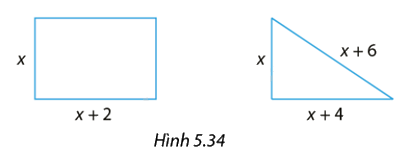
Hình chữ nhật và tam giác trong Hình 5.34 có cùng chu vi. Tính diện tích mỗi hình.
Đề bài
Hình chữ nhật và tam giác trong Hình 5.34 có cùng chu vi. Tính diện tích mỗi hình.
Phương pháp giải - Xem chi tiết
Tính cạnh x của mỗi hình bằng cách lập phương trình và giải, sau đó tính diện tích.
Lời giải chi tiết
Chu vi của hình chữ nhật là: \(\left( {x + x + 2} \right).2 = \left( {2x + 2} \right)2 = 4x + 4\)
Chu vi của hình tam giác là: \(x + \left( {x + 6} \right) + \left( {x + 4} \right) = 3x + 10\)
Mà chu vi của hình chữ nhật bằng chu vi hình tam giác, ta có phương trình:
\(\begin{array}{l}4x + 4 = 3x + 10\\4x - 3x = 10 - 4\\x = 6\end{array}\)
Vậy diện tích của hình chữ nhật là: \(6.\left( {6 + 2} \right) = 48\)
Diện tích của hình tam giác là: \(\frac{1}{2}.6.\left( {6 + 4} \right) = 30\)
Bài 5.29 trang 30 SGK Toán 8 yêu cầu chúng ta chứng minh đẳng thức đại số. Để giải bài toán này, chúng ta cần nắm vững các quy tắc biến đổi đại số, bao gồm quy tắc phân phối, quy tắc kết hợp và các tính chất của phép cộng, trừ, nhân, chia.
Chứng minh rằng: (a - b)(a + b) = a2 - b2
Để chứng minh đẳng thức trên, chúng ta có thể sử dụng phương pháp biến đổi vế trái (VT) để đưa về vế phải (VP).
(a - b)(a + b) = a(a + b) - b(a + b)
= a2 + ab - ba - b2
= a2 + ab - ab - b2
= a2 - b2
Vì (a - b)(a + b) = a2 - b2, nên đẳng thức được chứng minh.
Cho a = 5 và b = 3. Hãy tính giá trị của (a - b)(a + b) và a2 - b2 để kiểm tra lại đẳng thức.
(a - b)(a + b) = (5 - 3)(5 + 3) = 2 * 8 = 16
a2 - b2 = 52 - 32 = 25 - 9 = 16
Như vậy, (a - b)(a + b) = a2 - b2 với a = 5 và b = 3.
Đẳng thức (a - b)(a + b) = a2 - b2 là một công thức đại số quan trọng, thường được sử dụng trong các bài toán liên quan đến phân tích đa thức thành nhân tử và giải phương trình. Các em nên ghi nhớ và áp dụng công thức này một cách linh hoạt để giải quyết các bài toán tương tự.
Hãy chứng minh các đẳng thức sau:
Khi giải các bài tập về biến đổi đại số, các em cần chú ý:
Bài 5.29 trang 30 SGK Toán 8 là một bài tập cơ bản nhưng quan trọng, giúp các em củng cố kiến thức về các phép biến đổi đại số. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em sẽ hiểu rõ phương pháp giải bài tập này và tự tin hơn trong quá trình học tập môn Toán.