Chào mừng bạn đến với bài học về lý thuyết thể tích của hình chóp tam giác đều và hình chóp tứ giác đều trong chương trình Toán 8. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về chủ đề này.
Chúng ta sẽ cùng nhau tìm hiểu công thức tính thể tích, các yếu tố ảnh hưởng đến thể tích, và cách áp dụng lý thuyết vào giải các bài tập thực tế. Hãy cùng bắt đầu!
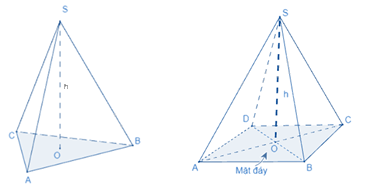
Công thức tính thể tích của hình chóp tam giác đều và hình chóp tứ giác đều
Công thức tính thể tích của hình chóp tam giác đều và hình chóp tứ giác đều
Thể tích của hình chóp tam giác đều (hình chóp tứ giác đều) bằng \(\frac{1}{3}\) diện tích đáy nhân với chiều cao.
\(V = \frac{1}{3}{S_{đáy}}.h\)
(V là thể tích, \({S_{đáy}}\) là diện tích đáy, \({S_{xq}}\) là diện tích xung quanh)
Ví dụ:
Cho hình chóp tứ giác đều sau:
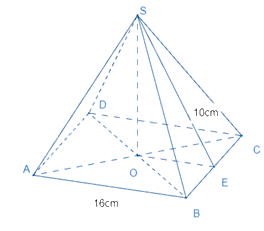
Chiều cao của hình chóp là: \(\sqrt {{{10}^2} - {{\left( {\frac{{16}}{2}} \right)}^2}} = \sqrt {100 - 64} = \sqrt {36} = 6(cm)\)
Thể tích của hình chóp là: \(V = \frac{1}{3}.6.16.16 = 512(c{m^3})\)
Trong chương trình Toán 8, kiến thức về hình học không gian đóng vai trò quan trọng, và việc nắm vững lý thuyết về thể tích hình chóp là nền tảng cho các bài toán phức tạp hơn. Bài viết này sẽ trình bày chi tiết lý thuyết về thể tích của hình chóp tam giác đều và hình chóp tứ giác đều, dựa trên nội dung sách giáo khoa Toán 8.
Hình chóp là một hình đa diện có một mặt đáy là một đa giác và các mặt bên là các tam giác có chung đỉnh. Đỉnh chung đó gọi là đỉnh của hình chóp. Chiều cao của hình chóp là khoảng cách từ đỉnh đến mặt phẳng đáy.
Thể tích của hình chóp được tính theo công thức:
V = (1/3) * B * h
Trong đó:
Hình chóp tam giác đều là hình chóp có đáy là tam giác đều và các mặt bên là các tam giác cân bằng nhau. Để tính thể tích của hình chóp tam giác đều, ta cần tính diện tích đáy (tam giác đều) và chiều cao của hình chóp.
Diện tích tam giác đều có cạnh a là: B = (a2√3)/4
Khi đó, thể tích của hình chóp tam giác đều là: V = (1/3) * (a2√3)/4 * h
Hình chóp tứ giác đều là hình chóp có đáy là hình vuông và các mặt bên là các tam giác cân bằng nhau. Để tính thể tích của hình chóp tứ giác đều, ta cần tính diện tích đáy (hình vuông) và chiều cao của hình chóp.
Diện tích hình vuông có cạnh a là: B = a2
Khi đó, thể tích của hình chóp tứ giác đều là: V = (1/3) * a2 * h
Bài 1: Tính thể tích của hình chóp tam giác đều có cạnh đáy bằng 5cm và chiều cao bằng 6cm.
Giải:
Diện tích đáy: B = (52√3)/4 = (25√3)/4 cm2
Thể tích: V = (1/3) * (25√3)/4 * 6 = (25√3)/2 cm3
Bài 2: Tính thể tích của hình chóp tứ giác đều có cạnh đáy bằng 4cm và chiều cao bằng 8cm.
Giải:
Diện tích đáy: B = 42 = 16 cm2
Thể tích: V = (1/3) * 16 * 8 = 128/3 cm3
Lý thuyết về thể tích hình chóp có ứng dụng rộng rãi trong thực tế, như tính thể tích của các công trình kiến trúc, các vật thể hình học, và trong các bài toán thực tế khác.
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về lý thuyết thể tích của hình chóp tam giác đều và hình chóp tứ giác đều. Hãy luyện tập thêm nhiều bài tập để nắm vững kiến thức và áp dụng vào giải các bài toán thực tế.