Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 8 của giaitoan.edu.vn. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Ở bài viết này, chúng ta sẽ cùng nhau đi sâu vào giải chi tiết các bài tập trong mục 2 trang 63, 64, 65 sách giáo khoa Toán 8. Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Cắt hình bình hành ABCD theo đường chéo AC
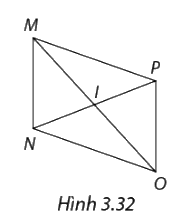
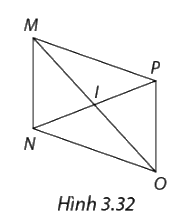
Trong hình 3.32, MONP là hình bình hành có MO và NP cắt nhau tại I và \(IN = 3cm,IO = 4cm,ON = 6cm.\) Tìm độ dài cạnh MP và đường chéo MO, NP.
Phương pháp giải:
Sử dụng định lí của hình bình hành.
Trong hình bình hành:
a) Các cạnh đối bằng nhau;
b) Các góc đối bằng nhau;
c) Hai đường chéo cắt nhau tại trung điểm mỗi đường.
Lời giải chi tiết:
Xét hình bình hành MNOP có \(MP = ON = 6cm.\)
I là giao điểm của MO và NP suy ra I là trung điểm của mỗi đường.
\( \Rightarrow IN = IP = 3cm;IO = IM = 4cm\)
\(NP = 2IN = 6cm;MO = 2IO = 8cm.\)
Cắt hình bình hành ABCD theo đường chéo AC và xếp chồng tam giác CDA lên tam giác ABC như nhình 3.28. Em hãy nhận xét về cạnh và góc của hai tam giác.
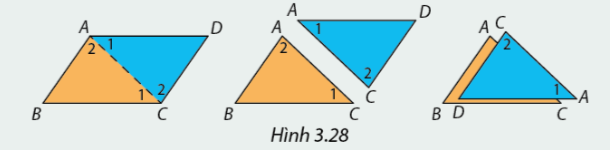
Sử dụng tính chất của hai đường thẳng song song, em hãy cho biết vì sao \(\widehat {{A_1}} = \widehat {{C_1}}\) và \(\widehat {{A_2}} = \widehat {{C_2}}\), từ đó giải thích vì sao \(\Delta ABC = \Delta CDA?\) Em có kết luận gì về độ dài các cặp cạnh \(AB\) và \(CD,\)\(BC\)và \(AD\), số đo cặp góc \(\widehat B\) và \(\widehat D?\)
Phương pháp giải:
Sử dụng tính chất của hai đường thẳng song song suy ra \(\widehat {{A_1}} = \widehat {{C_1}}\) và \(\widehat {{A_2}} = \widehat {{C_2}}\)
Từ đó suy ra \(\Delta ABC = \Delta CDA.\)
Các cặp góc, cặp cạnh tương ứng bằng nhau.
Lời giải chi tiết:
Có \(AD//BC\) nên \(\widehat {{A_1}} = \widehat {{C_1}}\) (so le trong).
Tương tự có \(AB//DC \Rightarrow \widehat {{A_2}} = \widehat {{C_2}}\) (so le trong)
Xét tam giác ABC và tam giác CDA có
\(\widehat {{A_1}} = \widehat {{C_1}}\)
\(AC\) chung
\(\widehat {{A_2}} = \widehat {{C_2}}\)
Vậy \(\Delta ABC = \Delta CDA\left( {g - c - g} \right)\)\( \Rightarrow AB = CD;BC = AD\)(hai cạnh tương ứng)
\(\widehat B = \widehat D\) (hai góc tương ứng).
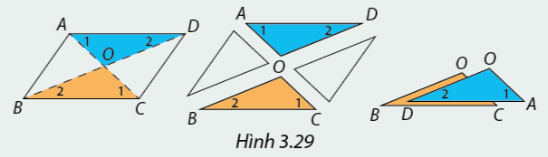
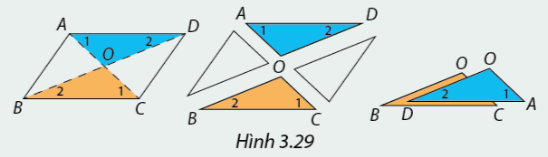
Cắt hình bình hành ABCD theo đường chéo AC, BD và xếp chồng tam giác OAD lên tam giác OCB như Hình 3.29. Em có nhận xét gì về cạnh và góc của hai tam giác?
Phương pháp giải:
Sử dụng tính chất song song, chứng minh \(\Delta OAD = \Delta OCB\left( {g - c - g} \right)\)
Suy ra các cặp cạnh, cặp góc tương ứng bằng nhau.
Lời giải chi tiết:
Ta thấy \(AD//BC \Rightarrow \widehat {{A_1}} = \widehat {{C_1}};\widehat {{A_2}} = \widehat {{C_2}}.\)
Mà \(AD = BC\) nên \(\Delta OAD = \Delta OCB\left( {g - c - g} \right)\)
Hai tam giác có các cặp cạnh tương ứng bằng nhau, các cặp góc tương ứng bằng nhau.
Cắt hình bình hành ABCD theo đường chéo AC và xếp chồng tam giác CDA lên tam giác ABC như nhình 3.28. Em hãy nhận xét về cạnh và góc của hai tam giác.
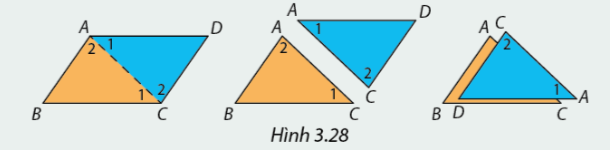
Sử dụng tính chất của hai đường thẳng song song, em hãy cho biết vì sao \(\widehat {{A_1}} = \widehat {{C_1}}\) và \(\widehat {{A_2}} = \widehat {{C_2}}\), từ đó giải thích vì sao \(\Delta ABC = \Delta CDA?\) Em có kết luận gì về độ dài các cặp cạnh \(AB\) và \(CD,\)\(BC\)và \(AD\), số đo cặp góc \(\widehat B\) và \(\widehat D?\)
Phương pháp giải:
Sử dụng tính chất của hai đường thẳng song song suy ra \(\widehat {{A_1}} = \widehat {{C_1}}\) và \(\widehat {{A_2}} = \widehat {{C_2}}\)
Từ đó suy ra \(\Delta ABC = \Delta CDA.\)
Các cặp góc, cặp cạnh tương ứng bằng nhau.
Lời giải chi tiết:
Có \(AD//BC\) nên \(\widehat {{A_1}} = \widehat {{C_1}}\) (so le trong).
Tương tự có \(AB//DC \Rightarrow \widehat {{A_2}} = \widehat {{C_2}}\) (so le trong)
Xét tam giác ABC và tam giác CDA có
\(\widehat {{A_1}} = \widehat {{C_1}}\)
\(AC\) chung
\(\widehat {{A_2}} = \widehat {{C_2}}\)
Vậy \(\Delta ABC = \Delta CDA\left( {g - c - g} \right)\)\( \Rightarrow AB = CD;BC = AD\)(hai cạnh tương ứng)
\(\widehat B = \widehat D\) (hai góc tương ứng).
Cắt hình bình hành ABCD theo đường chéo AC, BD và xếp chồng tam giác OAD lên tam giác OCB như Hình 3.29. Em có nhận xét gì về cạnh và góc của hai tam giác?
Phương pháp giải:
Sử dụng tính chất song song, chứng minh \(\Delta OAD = \Delta OCB\left( {g - c - g} \right)\)
Suy ra các cặp cạnh, cặp góc tương ứng bằng nhau.
Lời giải chi tiết:
Ta thấy \(AD//BC \Rightarrow \widehat {{A_1}} = \widehat {{C_1}};\widehat {{A_2}} = \widehat {{C_2}}.\)
Mà \(AD = BC\) nên \(\Delta OAD = \Delta OCB\left( {g - c - g} \right)\)
Hai tam giác có các cặp cạnh tương ứng bằng nhau, các cặp góc tương ứng bằng nhau.
Trong hình 3.32, MONP là hình bình hành có MO và NP cắt nhau tại I và \(IN = 3cm,IO = 4cm,ON = 6cm.\) Tìm độ dài cạnh MP và đường chéo MO, NP.
Phương pháp giải:
Sử dụng định lí của hình bình hành.
Trong hình bình hành:
a) Các cạnh đối bằng nhau;
b) Các góc đối bằng nhau;
c) Hai đường chéo cắt nhau tại trung điểm mỗi đường.
Lời giải chi tiết:
Xét hình bình hành MNOP có \(MP = ON = 6cm.\)
I là giao điểm của MO và NP suy ra I là trung điểm của mỗi đường.
\( \Rightarrow IN = IP = 3cm;IO = IM = 4cm\)
\(NP = 2IN = 6cm;MO = 2IO = 8cm.\)
Mục 2 của chương trình Toán 8 thường tập trung vào các kiến thức về hình học, cụ thể là các loại tứ giác đặc biệt như hình bình hành, hình chữ nhật, hình thoi, hình vuông. Việc nắm vững các tính chất, dấu hiệu nhận biết và các ứng dụng của chúng là vô cùng quan trọng để giải quyết các bài tập liên quan.
Mục 2 thường bao gồm các nội dung sau:
Để giải các bài tập trong mục 2, các em cần:
Bài tập: Cho hình chữ nhật ABCD, AB = 8cm, BC = 6cm. Tính độ dài đường chéo AC.
Giải:
Vì ABCD là hình chữ nhật nên góc ABC vuông. Áp dụng định lý Pitago vào tam giác ABC, ta có:
AC2 = AB2 + BC2 = 82 + 62 = 64 + 36 = 100
Suy ra AC = √100 = 10cm
Các bài tập trong mục 2 thường có các dạng sau:
Để đạt kết quả tốt nhất, các em nên:
Ngoài sách giáo khoa, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng với những hướng dẫn chi tiết trên, các em sẽ tự tin hơn khi giải các bài tập trong mục 2 trang 63, 64, 65 SGK Toán 8. Chúc các em học tập tốt!