Chào mừng bạn đến với bài học về Lý thuyết Xác suất của biến cố ngẫu nhiên trong chương trình Toán 8. Đây là một phần kiến thức quan trọng, giúp bạn làm quen với những khái niệm cơ bản của lý thuyết xác suất, một lĩnh vực ứng dụng rộng rãi trong đời sống.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu cùng với các bài tập thực hành đa dạng để bạn có thể nắm vững kiến thức này một cách hiệu quả.
Xác suất của biến cố ngẫu nhiên là gì?
1. Biến cố, biến cố ngẫu nhiên
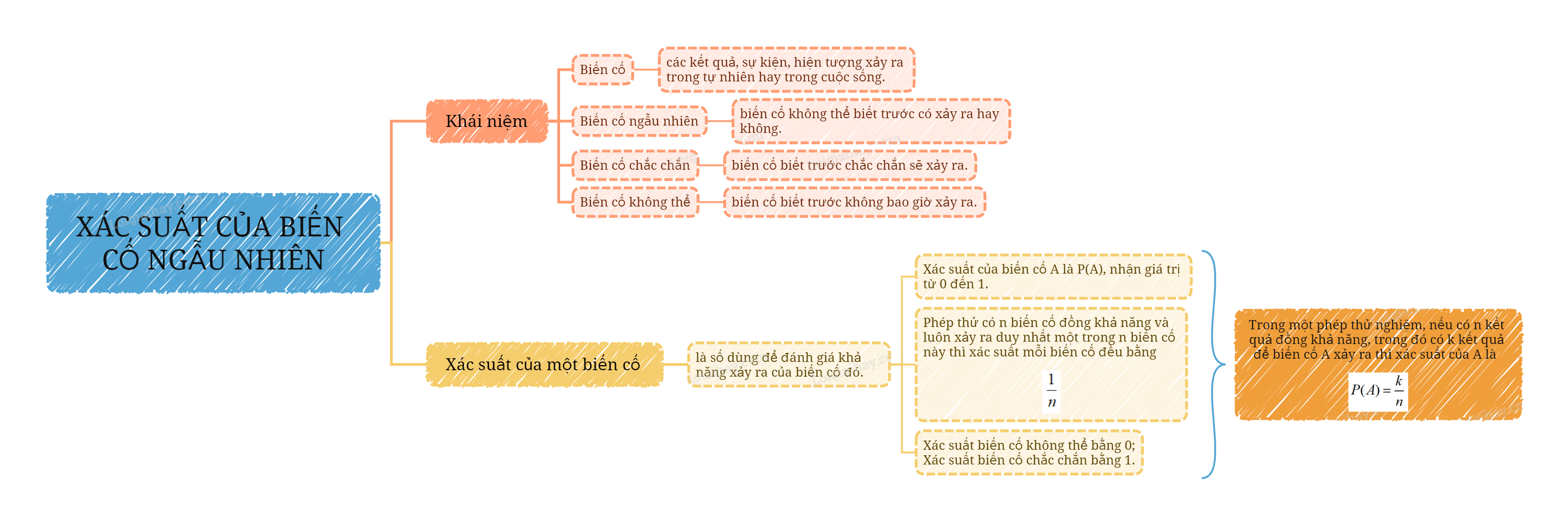
- Biến cố là các kết quả, sự kiện, hiện tượng xảy ra trong tự nhiên hay trong cuộc sống.
- Biến cố ngẫu nhiên là biến cố không thể biết trước có xảy ra hay không.
- Biến cố biết trước chắc chắn sẽ xảy ra được gọi là biến cố chắc chắn.
- Biến cố biết trước không bao giờ xảy ra được gọi là biến cố không thể.
2. Xác suất của một biến cố
Xác suất của một biến cố là số được dùng để đánh giá khả năng xảy ra của biến cố đó.
- Xác suất của biến cố A, kí hiệu là P(A), là một số nhận giá trị từ 0 đến 1.
- Nếu phép thử nghiệm có n biến cố đồng khả năng và luôn xảy ra duy nhất một trong n biến cố này thì xác suất của mỗi biến cố đều bằng \(\frac{1}{n}\).
- Xác suất của biến cố không thể bằng 0. Xác suất của biến cố chắc chắn bằng 1.
Tổng quát:
Trong một phép thử nghiệm, nếu có n kết quả đồng khả năng, trong đó có k kết quả để biến cố A xảy ra thì xác suất của A là \(P(A) = \frac{k}{n}\).
Để tiện cho tính toán, so sánh, người ta thường viết xác suất của biến cố dưới dạng số thập phân hoặc dạng phần trăm.
Xác suất là một khái niệm toán học dùng để đo lường khả năng xảy ra của một sự kiện ngẫu nhiên. Trong chương trình Toán 8, chúng ta bắt đầu làm quen với những khái niệm cơ bản nhất của lý thuyết xác suất, tập trung vào các biến cố ngẫu nhiên và cách tính xác suất của chúng.
Một biến cố ngẫu nhiên là một sự kiện mà kết quả của nó không thể đoán trước một cách chắc chắn. Ví dụ:
Không gian mẫu (ký hiệu là Ω) là tập hợp tất cả các kết quả có thể xảy ra của một thí nghiệm ngẫu nhiên. Ví dụ:
Xác suất của một biến cố A (ký hiệu là P(A)) là tỷ lệ giữa số các kết quả thuận lợi cho A và tổng số các kết quả có thể xảy ra (số phần tử của không gian mẫu). Công thức tính xác suất:
P(A) = (Số kết quả thuận lợi cho A) / (Tổng số kết quả có thể xảy ra)
Ví dụ 1: Gieo một con xúc xắc. Tính xác suất để xuất hiện mặt 6.
Giải:
Ví dụ 2: Đúc một đồng xu. Tính xác suất để xuất hiện mặt ngửa.
Giải:
Trong một số trường hợp, chúng ta có thể sử dụng các quy tắc sau để tính xác suất:
Để củng cố kiến thức, hãy thử giải các bài tập sau:
Lý thuyết Xác suất của biến cố ngẫu nhiên là một phần kiến thức quan trọng trong chương trình Toán 8. Việc nắm vững các khái niệm và công thức cơ bản sẽ giúp bạn giải quyết các bài toán liên quan một cách dễ dàng và hiệu quả. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.
Chúc bạn học tốt!