Chào mừng bạn đến với bài học về Lý thuyết Hình thoi trong chương trình SGK Toán 8. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về hình thoi, giúp bạn hiểu rõ định nghĩa, tính chất, dấu hiệu nhận biết và các ứng dụng thực tế của hình thoi trong giải toán.
Tại giaitoan.edu.vn, chúng tôi luôn cố gắng mang đến những bài giảng chất lượng, dễ hiểu và phù hợp với mọi trình độ học sinh. Hãy cùng chúng tôi khám phá thế giới hình học thú vị này!
Hình thoi là gì?
1. Khái niệm
Hình thoi là tứ giác có bốn cạnh bằng nhau.
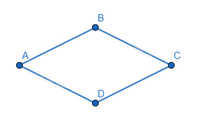
Lưu ý: Hình thoi là hình bình hành.
2. Tính chất
- Các cạnh đối song song
- Các góc đối bằng nhau
- Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường
- Hai đường chéo là các đường phân giác của các góc ở đỉnh.
3. Dấu hiệu nhận biết hình thoi
a. Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
b. Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
c. Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
Ví dụ:
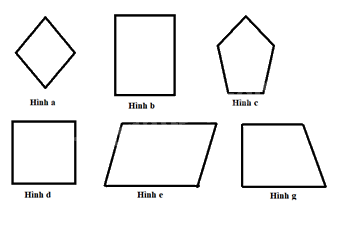
Hình a, d là hình thoi.
Hình thoi là một tứ giác đặc biệt, đóng vai trò quan trọng trong chương trình Hình học lớp 8. Việc nắm vững lý thuyết về hình thoi không chỉ giúp học sinh giải quyết các bài tập trong sách giáo khoa mà còn là nền tảng để tiếp thu các kiến thức nâng cao hơn trong tương lai.
Hình thoi là tứ giác có bốn cạnh bằng nhau.
Lưu ý:
Hình thoi có những tính chất quan trọng sau:
Có những dấu hiệu sau để nhận biết một tứ giác là hình thoi:
Lý thuyết hình thoi được ứng dụng rộng rãi trong giải toán, đặc biệt là trong các bài toán liên quan đến tính diện tích, chu vi, và chứng minh các tính chất hình học.
Bài tập 1: Cho hình thoi ABCD có cạnh AB = 5cm và đường chéo AC = 8cm. Tính độ dài đường chéo BD.
Giải:
Vì ABCD là hình thoi nên hai đường chéo AC và BD vuông góc với nhau tại trung điểm O của mỗi đường. Do đó, tam giác AOB là tam giác vuông tại O. Áp dụng định lý Pitago trong tam giác AOB, ta có:
AO2 + BO2 = AB2
(AC/2)2 + BO2 = 52
(8/2)2 + BO2 = 25
42 + BO2 = 25
16 + BO2 = 25
BO2 = 9
BO = 3cm
Vậy BD = 2 * BO = 2 * 3 = 6cm.
Bài tập 2: Chứng minh rằng các đường phân giác của các góc trong một hình thoi song song với các cạnh đối diện.
Giải:
Gọi hình thoi là ABCD, các đường phân giác của các góc A, B, C, D lần lượt là AE, BF, CG, DH. Ta cần chứng minh AE // CD và BF // AD.
Vì ABCD là hình thoi nên AB // CD và AD // BC. Do đó, góc A + góc D = 180o và góc B + góc C = 180o.
Vì AE là đường phân giác của góc A và DH là đường phân giác của góc D nên góc EAD = góc A/2 và góc ADH = góc D/2.
Suy ra góc EAD + góc ADH = (góc A + góc D)/2 = 180o/2 = 90o.
Do đó, AE // CD (vì góc EAD + góc ADC = 90o + góc ADC = 180o).
Tương tự, ta có thể chứng minh BF // AD.
Để nắm vững lý thuyết hình thoi, bạn nên luyện tập thêm nhiều bài tập khác nhau. Hãy tìm các bài tập trong sách giáo khoa, sách bài tập, hoặc trên các trang web học toán online như giaitoan.edu.vn.
Lý thuyết hình thoi là một phần quan trọng của chương trình Hình học lớp 8. Việc hiểu rõ định nghĩa, tính chất, dấu hiệu nhận biết và các ứng dụng của hình thoi sẽ giúp bạn giải quyết các bài toán một cách hiệu quả và tự tin hơn. Chúc bạn học tốt!