Bài viết này cung cấp lý thuyết đầy đủ và chi tiết về trường hợp đồng dạng góc - góc trong chương trình Toán 8, bám sát nội dung sách giáo khoa. Chúng ta sẽ cùng nhau tìm hiểu điều kiện để hai tam giác đồng dạng, cách áp dụng lý thuyết vào giải bài tập và những lưu ý quan trọng.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán, mang đến những kiến thức chất lượng và phương pháp học tập hiệu quả.
Trường hợp đồng dạng góc - góc là gì?
Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
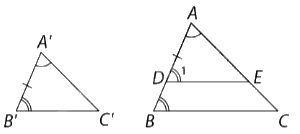
\(\begin{array}{l}\Delta ABC,\Delta A'B'C',\widehat {A'} = \widehat A,\widehat {B'} = \widehat B\\ \Rightarrow \Delta A'B'C' \backsim \Delta ABC\end{array}\)
Nhận xét: Tỉ số hai đường phân giác tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng.
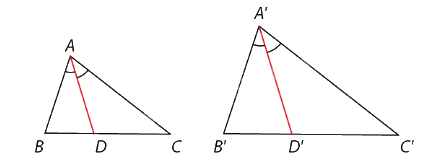
Nếu \(\Delta A'B'C' \backsim \Delta ABC\) với tỉ số đồng dạng k thì \(\frac{{A'D'}}{{AD}} = k\).
Trong chương trình Toán 8, việc nắm vững các trường hợp đồng dạng tam giác là vô cùng quan trọng. Một trong những trường hợp đó là trường hợp đồng dạng góc - góc. Bài viết này sẽ đi sâu vào lý thuyết này, cung cấp các ví dụ minh họa và bài tập để bạn có thể hiểu rõ và áp dụng vào giải toán.
Hai tam giác được gọi là đồng dạng nếu chúng có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ.
Nếu hai tam giác có hai góc tương ứng bằng nhau thì hai tam giác đó đồng dạng.
Ví dụ: Xét tam giác ABC và tam giác A'B'C' có:
Thì tam giác ABC đồng dạng với tam giác A'B'C' (ký hiệu: ΔABC ~ ΔA'B'C').
Nếu một tam giác vuông có một góc nhọn bằng góc nhọn của tam giác vuông khác thì hai tam giác đó đồng dạng.
Trường hợp đồng dạng góc - góc được sử dụng để:
Bài 1: Cho tam giác ABC và tam giác MNP có ∠A = ∠M = 60° và ∠B = ∠N = 80°. Chứng minh rằng ΔABC ~ ΔMNP.
Giải:
Vì ∠A = ∠M và ∠B = ∠N nên theo trường hợp đồng dạng góc - góc, ta có ΔABC ~ ΔMNP.
Bài 2: Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D. Biết ∠B = 40° và ∠E = 40°. Chứng minh rằng ΔABC ~ ΔDEF.
Giải:
Vì ΔABC và ΔDEF là các tam giác vuông và ∠B = ∠E = 40° nên theo hệ quả của trường hợp đồng dạng góc - góc, ta có ΔABC ~ ΔDEF.
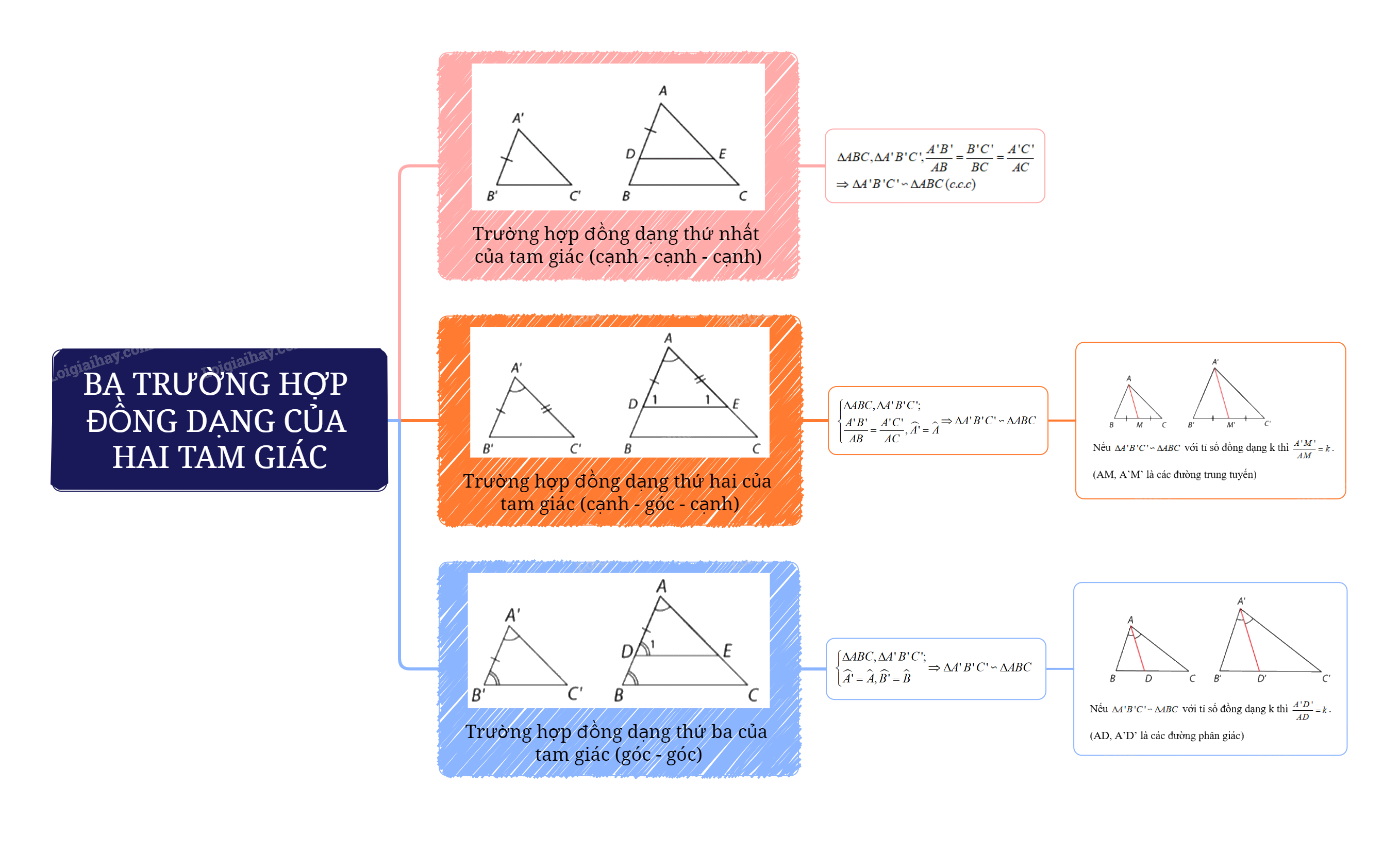
Ngoài trường hợp đồng dạng góc - góc, còn có hai trường hợp đồng dạng khác là trường hợp cạnh - cạnh - cạnh (c-c-c) và trường hợp cạnh - góc - cạnh (c-g-c). Việc nắm vững cả ba trường hợp này sẽ giúp bạn giải quyết mọi bài toán liên quan đến tam giác đồng dạng.
Trường hợp đồng dạng góc - góc là một công cụ quan trọng trong việc chứng minh hai tam giác đồng dạng. Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về lý thuyết này và có thể áp dụng vào giải toán một cách hiệu quả. Hãy luyện tập thêm nhiều bài tập để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.
Giaitoan.edu.vn luôn cập nhật những kiến thức Toán học mới nhất và cung cấp các bài giảng chất lượng cao. Hãy truy cập website của chúng tôi để khám phá thêm nhiều tài liệu học tập hữu ích.