Chào mừng các em học sinh đến với bài giải chi tiết mục 1 trang 62, 63 sách giáo khoa Toán 8. Tại giaitoan.edu.vn, chúng tôi cung cấp các lời giải bài tập Toán 8 chính xác, dễ hiểu, giúp các em học tập hiệu quả và đạt kết quả tốt nhất.
Bài giải này được xây dựng dựa trên chương trình học Toán 8 hiện hành, đảm bảo tính chính xác và phù hợp với nội dung sách giáo khoa.
Giải thích vì sao trong Hình 6.76, \(\Delta A'B'C'\) đồng dạng với \(\Delta ABC\)?
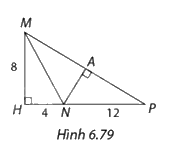
Chứng minh rằng trong Hình 6.79, \(\Delta HMN\) đồng dạng với \(\Delta HPM\) và \(\Delta APN\).
Phương pháp giải:
Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
Nếu hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
Lời giải chi tiết:
Xét hai tam giác vuông \(HMN\) và \(HPM\), ta có:
\(\frac{{HM}}{{HP}} = \frac{{HN}}{{HM}} = \frac{1}{2}\)
\(\widehat H\) chung
=> \(\Delta HMN\)∽\(\Delta HPM\)
Xét hai tam giác vuông \(HMN\) và \(APN\), ta có:
\(\widehat H = \widehat {NAP} = 90^\circ \)
\(\widehat {HMN} = \widehat {APN}\) (do \(\Delta HMN\)∽\(\Delta HPM\))
=> \(\Delta HMN\)∽\(\Delta APN\) (cạnh huyền-góc nhọn)
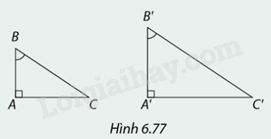
Giải thích vì sao trong Hình 6.77, \(\Delta A'B'C'\) đồng dạng với \(\Delta ABC\)?
Phương pháp giải:
Áp dụng trường hợp đồng dạng góc-góc để giải thích
Lời giải chi tiết:
Xét tam giác \(ABC\) và tam giác \(A'B'C'\), có:
\(\begin{array}{l}\widehat A = \widehat {A'} = 90^\circ \\\widehat B = \widehat {B'}\left( {gt} \right)\end{array}\)
=> \(\Delta ABC\)∽\(\Delta A'B'C'\)
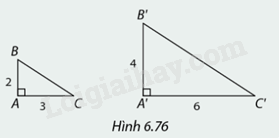
Giải thích vì sao trong Hình 6.76, \(\Delta A'B'C'\) đồng dạng với \(\Delta ABC\)?
Phương pháp giải:
Áp dụng trường hợp đồng dạng cạnh-góc-cạnh của tam giác để giải thích
Lời giải chi tiết:
Xét tam giác \(ABC\) và tam giác \(A'B'C'\), có:
\(\widehat A = \widehat {A'} = 90^\circ \)
\(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{1}{2}\)
=> \(\Delta ABC\)∽\(\Delta A'B'C'\)
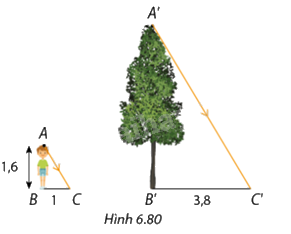
Vào một thời điểm trong ngày, bóng của bạn An trên mặt đất là \(BC = 1m\), còn bóng cây \(A'B'\) là \(B'C' = 3,8m\) (Hình 6.80). Biết An cao 1,6m, hỏi cây cao bao nhiêu mét? Làm tròn kết quả đến hàng phần mười.
Phương pháp giải:
Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
Nếu hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
Lời giải chi tiết:
Ta có: \(\Delta ABC\)∽\(\Delta A'B'C'\), nên suy ra tỉ số đồng dạng:
\(\begin{array}{l}\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\\ \Leftrightarrow \frac{{1,6}}{{A'B'}} = \frac{1}{{3,8}}\\ \Rightarrow A'B' = 6,08\end{array}\)
Vậy cây cao 6,08 m.
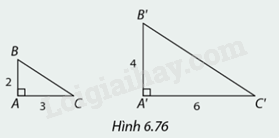
Giải thích vì sao trong Hình 6.76, \(\Delta A'B'C'\) đồng dạng với \(\Delta ABC\)?
Phương pháp giải:
Áp dụng trường hợp đồng dạng cạnh-góc-cạnh của tam giác để giải thích
Lời giải chi tiết:
Xét tam giác \(ABC\) và tam giác \(A'B'C'\), có:
\(\widehat A = \widehat {A'} = 90^\circ \)
\(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{1}{2}\)
=> \(\Delta ABC\)∽\(\Delta A'B'C'\)
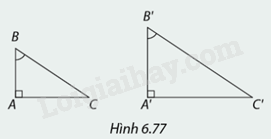
Giải thích vì sao trong Hình 6.77, \(\Delta A'B'C'\) đồng dạng với \(\Delta ABC\)?
Phương pháp giải:
Áp dụng trường hợp đồng dạng góc-góc để giải thích
Lời giải chi tiết:
Xét tam giác \(ABC\) và tam giác \(A'B'C'\), có:
\(\begin{array}{l}\widehat A = \widehat {A'} = 90^\circ \\\widehat B = \widehat {B'}\left( {gt} \right)\end{array}\)
=> \(\Delta ABC\)∽\(\Delta A'B'C'\)
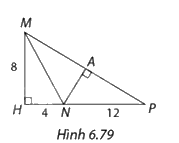
Chứng minh rằng trong Hình 6.79, \(\Delta HMN\) đồng dạng với \(\Delta HPM\) và \(\Delta APN\).
Phương pháp giải:
Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
Nếu hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
Lời giải chi tiết:
Xét hai tam giác vuông \(HMN\) và \(HPM\), ta có:
\(\frac{{HM}}{{HP}} = \frac{{HN}}{{HM}} = \frac{1}{2}\)
\(\widehat H\) chung
=> \(\Delta HMN\)∽\(\Delta HPM\)
Xét hai tam giác vuông \(HMN\) và \(APN\), ta có:
\(\widehat H = \widehat {NAP} = 90^\circ \)
\(\widehat {HMN} = \widehat {APN}\) (do \(\Delta HMN\)∽\(\Delta HPM\))
=> \(\Delta HMN\)∽\(\Delta APN\) (cạnh huyền-góc nhọn)
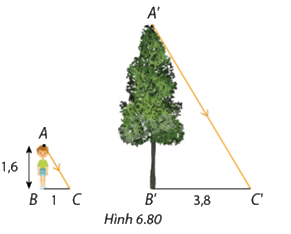
Vào một thời điểm trong ngày, bóng của bạn An trên mặt đất là \(BC = 1m\), còn bóng cây \(A'B'\) là \(B'C' = 3,8m\) (Hình 6.80). Biết An cao 1,6m, hỏi cây cao bao nhiêu mét? Làm tròn kết quả đến hàng phần mười.
Phương pháp giải:
Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
Nếu hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
Lời giải chi tiết:
Ta có: \(\Delta ABC\)∽\(\Delta A'B'C'\), nên suy ra tỉ số đồng dạng:
\(\begin{array}{l}\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\\ \Leftrightarrow \frac{{1,6}}{{A'B'}} = \frac{1}{{3,8}}\\ \Rightarrow A'B' = 6,08\end{array}\)
Vậy cây cao 6,08 m.
Mục 1 trang 62, 63 SGK Toán 8 thường chứa các bài tập về các kiến thức cơ bản của chương trình đại số hoặc hình học. Để giải quyết các bài tập này một cách hiệu quả, học sinh cần nắm vững các định nghĩa, tính chất và định lý liên quan.
Thông thường, mục này sẽ tập trung vào một trong các chủ đề sau:
Để thu gọn đa thức, ta cần thực hiện các phép toán cộng, trừ các đơn thức đồng dạng. Ví dụ:
3x2 + 2x - 5x2 + x + 1 = (3x2 - 5x2) + (2x + x) + 1 = -2x2 + 3x + 1
Ta có thể sử dụng các phương pháp sau:
ax + bx = x(a + b)a2 - b2 = (a - b)(a + b)ax + ay + bx + by = a(x + y) + b(x + y) = (x + y)(a + b)Ta có thể sử dụng tính chất của tỉ lệ thức: a/b = c/d => ad = bc
Bài tập: Giải phương trình: (x + 2)(x - 3) = 0
Giải:
Phương trình tương đương với:
x + 2 = 0 hoặc x - 3 = 0
x = -2 hoặc x = 3
Vậy phương trình có hai nghiệm là x = -2 và x = 3.
Giaitoan.edu.vn cung cấp:
Hãy truy cập giaitoan.edu.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập Toán 8 hữu ích!
| Chủ đề | Ví dụ |
|---|---|
| Thu gọn đa thức | 2x2 + 3x - x2 + 5x - 2 |
| Phân tích đa thức | x2 - 4 |
| Đây chỉ là một vài ví dụ minh họa. | |