Bài viết này cung cấp lời giải chi tiết và dễ hiểu cho bài tập 3.27 trang 80 sách giáo khoa Toán 8. Chúng tôi sẽ giúp bạn hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Giaitoan.edu.vn là địa chỉ học toán online uy tín, cung cấp đầy đủ các bài giải Toán 8, Toán 7, Toán 6 và các lớp khác.
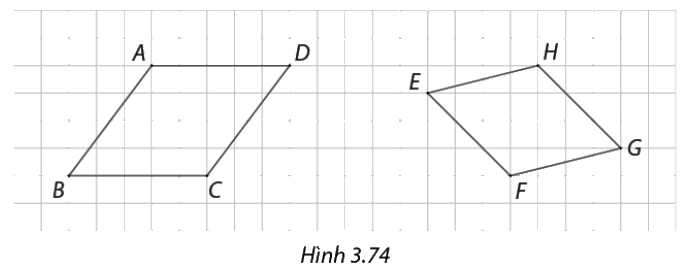
Trong Hình 3.74, tứ giác nào là hình thoi?
Đề bài
Trong Hình 3.74, tứ giác nào là hình thoi?
Phương pháp giải - Xem chi tiết
Dựa vào dấu hiệu nhận biết hình thoi để xác định tứ giác nào là hình thoi:
Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi
Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
Lời giải chi tiết
Gọi 1 ô li là 1cm, ta có:
Tứ giác \(ABCD\) là hình thoi vì có \(AB = BC = CD = DA\).
\(\begin{array}{l}AB = CD = \sqrt {{4^2} + {3^2}} = 5\\ = > AB = CD = AD = BC = 5\end{array}\)
Tứ giác \(EFGH\) không phải hình thoi vì không có bốn cạnh bằng nhau.
\(\begin{array}{l}EH = FG = \sqrt {{4^2} + {1^2}} = \sqrt {17} \\EF = HG = \sqrt {{3^2} + {3^2}} = 3\sqrt 2 \end{array}\)
Bài 3.27 trang 80 SGK Toán 8 thuộc chương trình học về hình học, cụ thể là phần kiến thức liên quan đến tứ giác. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản sau:
Bài 3.27 thường yêu cầu học sinh vận dụng kiến thức về tổng các góc trong một tứ giác để tính góc chưa biết, hoặc chứng minh một tứ giác là một loại tứ giác đặc biệt nào đó. Đôi khi, bài tập cũng yêu cầu học sinh sử dụng các tính chất của các loại tứ giác đặc biệt để giải quyết vấn đề.
Để giải bài 3.27 trang 80 SGK Toán 8, chúng ta cần phân tích kỹ đề bài, xác định các yếu tố đã biết và yếu tố cần tìm. Sau đó, áp dụng các kiến thức và công thức phù hợp để giải quyết bài toán. Dưới đây là một ví dụ minh họa:
Cho tứ giác ABCD có góc A = 80 độ, góc B = 100 độ, góc C = 120 độ. Tính góc D.
Giải:
Áp dụng tính chất tổng các góc trong một tứ giác, ta có:
Góc A + Góc B + Góc C + Góc D = 360 độ
80 độ + 100 độ + 120 độ + Góc D = 360 độ
300 độ + Góc D = 360 độ
Góc D = 360 độ - 300 độ
Góc D = 60 độ
Vậy, góc D của tứ giác ABCD bằng 60 độ.
Ngoài bài 3.27, còn rất nhiều bài tập tương tự liên quan đến tứ giác. Để giải các bài tập này, học sinh có thể áp dụng các phương pháp sau:
Để củng cố kiến thức và kỹ năng giải bài tập về tứ giác, học sinh nên luyện tập thêm các bài tập khác trong SGK và các tài liệu tham khảo. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững kiến thức và tự tin hơn khi giải các bài tập khó.
Bài 3.27 trang 80 SGK Toán 8 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về tứ giác và các tính chất của nó. Bằng cách nắm vững kiến thức cơ bản và áp dụng các phương pháp giải phù hợp, học sinh có thể giải quyết bài tập này một cách dễ dàng và hiệu quả. Giaitoan.edu.vn hy vọng bài viết này đã cung cấp cho bạn những thông tin hữu ích và giúp bạn học tốt môn Toán 8.